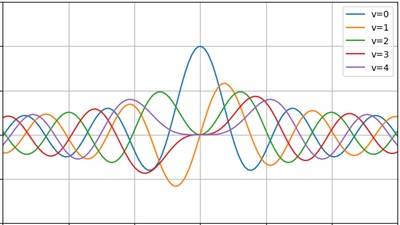
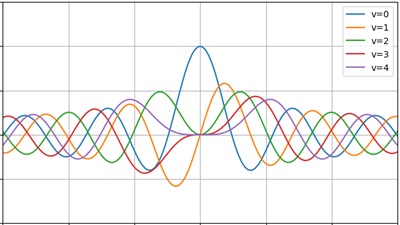
ベッセル関数とは
ベッセルの微分方程式
ヘルムホルツ方程式と呼ばれる式に対し、円柱座標を適用させて得られる方程式に次に示されるような微分方程式があります。

上記の微分方程式をベッセルの微分方程式、または第一種ベッセル関数などといったりします。もともとは天文学者ベッセルによる惑星の軌道運動の考察研究から始まったもののようですがその後の数学者や物理学者たちによって様々な物理現象を解明するに至ったという背景があり、そのためそれらに関連するものも含めてベッセル関数と呼ぶようになったようです。ベッセル関数はヘルムホルツ方程式やラプラス方程式に対して、円筒座標系や極座標系などを適用した場合の分離解として応用され、例えば薄い円形膜の振動の解析などに利用されます。このカテゴリーでは第1種ベッセル方程式の導入とその解の導出、そして第2種ベッセル、ハンケル関数といった変形ベッセル、さらにはその物理的な応用としての円形膜の振動などといった事項を取り扱っていきます。
惑星軌道運動の数理解析

ベッセル関数はドイツの天文学者ベッセルによって行われた惑星の軌道運動に関しての解析的な研究から始まった一連の数学関数群のひとくくりのものをさします。ここでは歴史的背景を考慮してケプラー方程式の導出と、そこから導かれる、上記に示したベッセルの微分方程式そのものの導出までの詳細な過程を考察していきます。
ケプラー方程式の導出
図は惑星軌道運動を描いたものです。惑星の運動を表現する場合まず楕円軌道上の点![]() を考え、この
を考え、この![]() は太陽
は太陽![]() の引力のもとその焦点を
の引力のもとその焦点を![]() としある時点における動径ベクトル
としある時点における動径ベクトル![]() の描く面積が時間
の描く面積が時間 の時点において比例する楕円軌道を描くものと考えます。
の時点において比例する楕円軌道を描くものと考えます。
![]()
![]() を楕円の長軸
を楕円の長軸![]() とし、短軸を
とし、短軸を![]() 、離心率を
、離心率を![]() とします。また真円上を回転運動するものと考える点を
とします。また真円上を回転運動するものと考える点を![]() と置きこの点は楕円軌道上を動く点
と置きこの点は楕円軌道上を動く点![]() とは
とは![]() 及び
及び![]() で同時に一致するものと考えます。このとき図中の角度
で同時に一致するものと考えます。このとき図中の角度![]() 、
、![]() 、
、![]() はそれぞれ以下のようになります。
はそれぞれ以下のようになります。

この関係において惑星が楕円上を1週するときの周期を![]() とすれば次のような関係が導かれます。
とすれば次のような関係が導かれます。
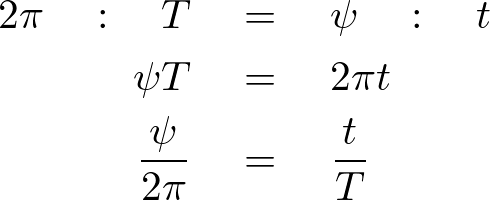
上記相似式と画像の色掛け部分の面積![]() との関係は以下のようにおけます。
との関係は以下のようにおけます。
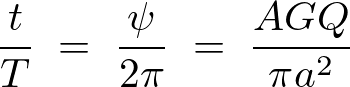
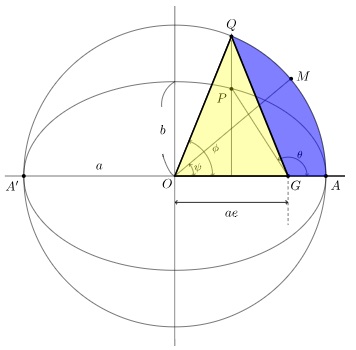
この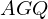 の面積は扇形
の面積は扇形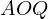 の面積から三角形
の面積から三角形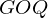 の面積を引いたものになるので次のようになります。
の面積を引いたものになるので次のようになります。
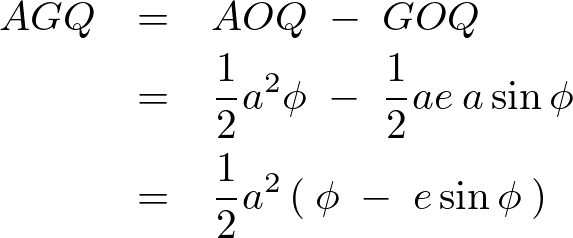
また先ほどの関係式より、
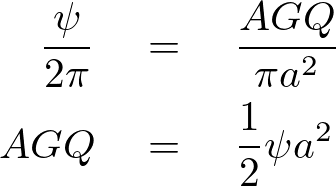
これを比較計算すると![]() と
と![]() に関して次のような関係式が求まることになります。
に関して次のような関係式が求まることになります。
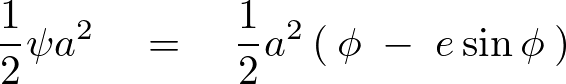
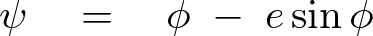
さらにここで先ほどの![]() に関しての式を次のようにし、でてきたを
に関しての式を次のようにし、でてきたを![]() を
を![]() とおきます。
とおきます。
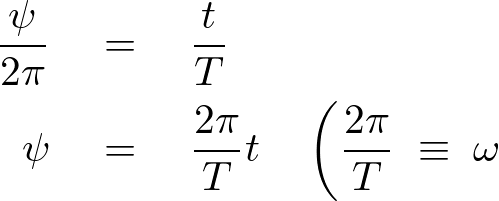
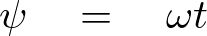
これによりケプラーの式は![]() を考えている楕円軌道の離心率、
を考えている楕円軌道の離心率、![]() を角速度、
を角速度、![]() を近日点通過後の時間として以下のように求められることになります。
を近日点通過後の時間として以下のように求められることになります。

ベッセル方程式の導出
今ここで上記ケプラー方程式に対して![]() で微分をほどこします。
で微分をほどこします。
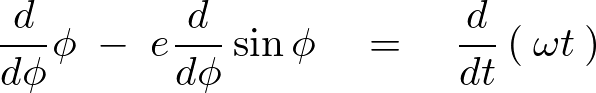
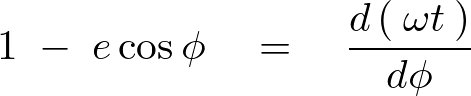
さらにケプラー式からベッセル方程式を導いていくために便宜上として次のようにおくことにします。
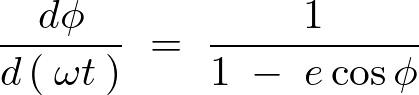
上記式右辺に関しての関数は![]() の連続な周期関数となるので一様収束可能なフーリエ級数として表現することが可能になります。
の連続な周期関数となるので一様収束可能なフーリエ級数として表現することが可能になります。

上記フーリエ級数の係数![]() および
および![]() は一般的に次のように表せられるものになります。
は一般的に次のように表せられるものになります。

なおまた同様に一般的にいえば、フーリエ級数展開式というのは以下のように表せられます。
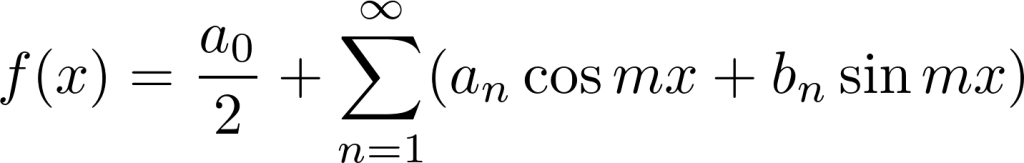
なのでこれより、
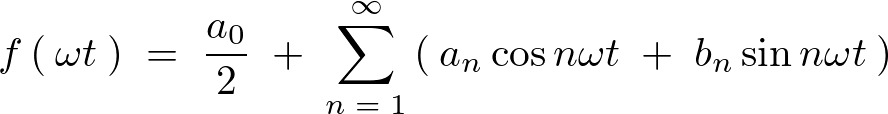
これに当てはめてそれぞれの第1項から第3項までを導出していきます。
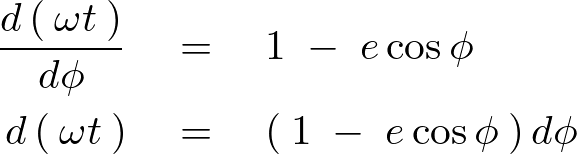
より、まず第1項の![]() から行っていきます。
から行っていきます。
第1項 の計算
の計算

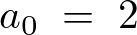
第2項 の計算
の計算
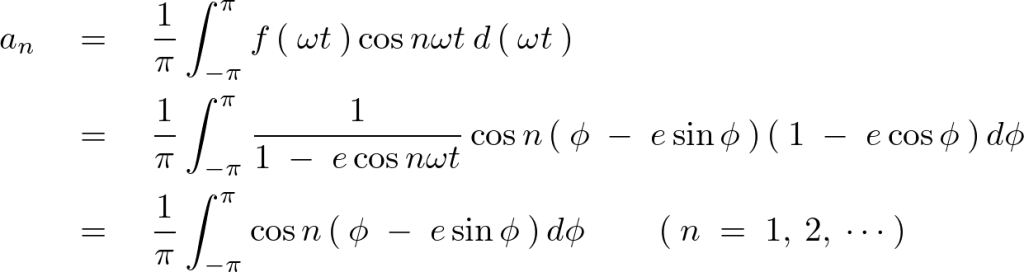
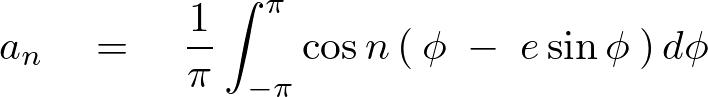
第3項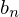 の計算
の計算
これに関して、今ケプラーの方程式を思い出せば、![]() は遇関数なので奇関数の
は遇関数なので奇関数の![]() 項の
項の![]() はキャンセルできます(フーリエ級数展開の項目を参照)。
はキャンセルできます(フーリエ級数展開の項目を参照)。
なので第3項の![]() は次のようになります。
は次のようになります。
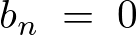
まとめれば以下のようになります。
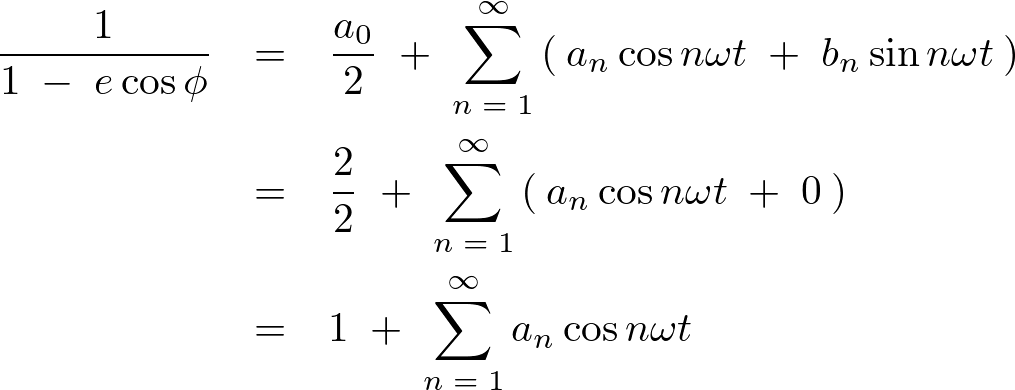
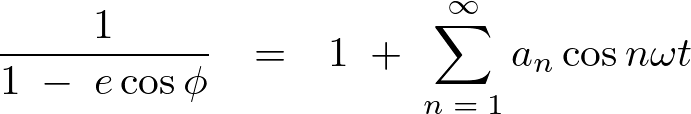
ここで以下の式、
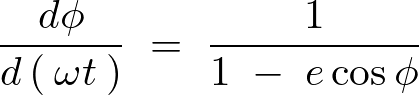
を思い出せば次のようになります。
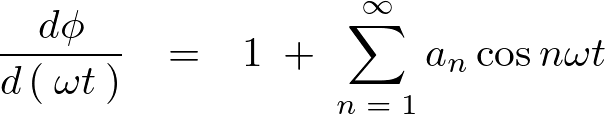
この式の両辺を![]() で積分します。
で積分します。
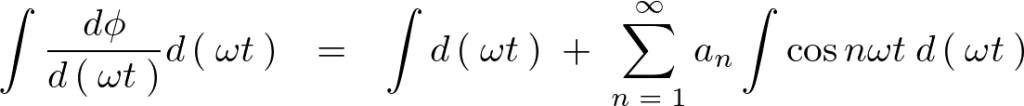
ここで右辺第2項の積分については以下のように置換をしています。
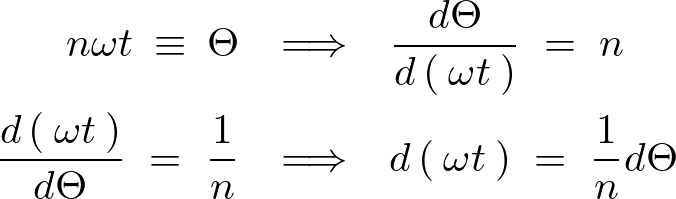
これを使って代入していけば次のように求まることになります。
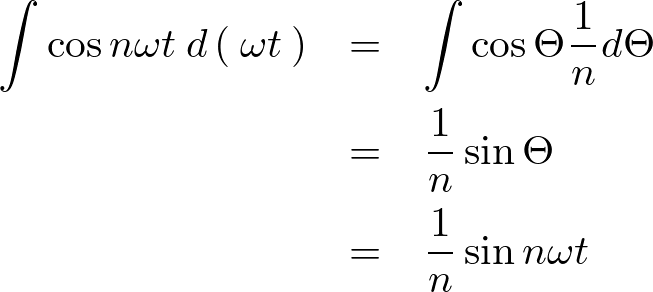
これを元の式に代入して計算していきます。
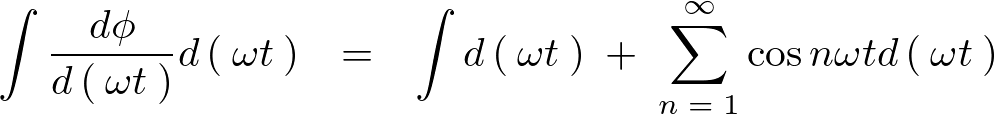
以下のように求まります。
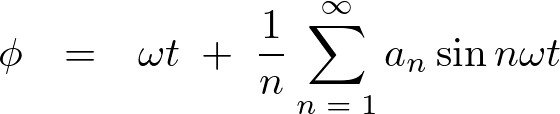
これにより上記式から離心近点離角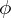 が
が のフーリエ級数として求められたということがわかります(参考:薮下信 特殊関数とその応用POD版より)。
のフーリエ級数として求められたということがわかります(参考:薮下信 特殊関数とその応用POD版より)。
さらに上記によりフーリエ係数![]() は
は![]() と
と![]() の関数と見て取れるので今これを
の関数と見て取れるので今これを![]() という関数とみなしてそれを
という関数とみなしてそれを![]() とおき、
とおき、![]() のかわりに
のかわりに![]() とおいてこれを微分していきます。
とおいてこれを微分していきます。
いったんここで三角関数の偶奇性により積分範囲を以下のようにして2倍します。

これを![]() で微分していきます。
で微分していきます。
まずチェイン(連鎖律の適用)させるために上記方程式を次のようにおきます。
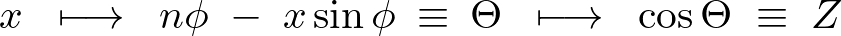
それぞれを微分します。
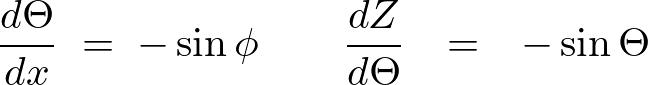
連鎖律を適用します。

これにより![]() の一階微分
の一階微分![]() は次のようになります。
は次のようになります。
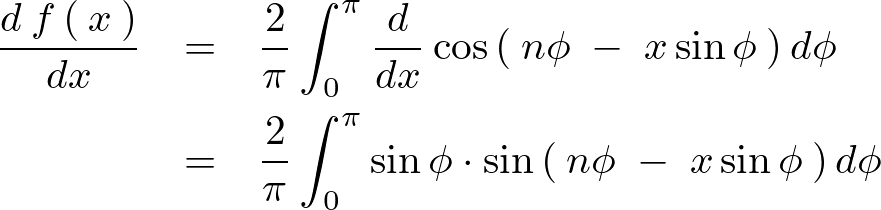
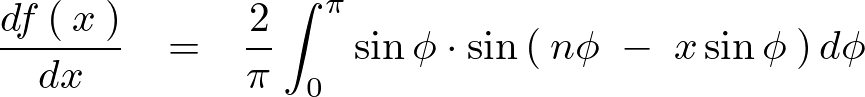
上記式をさらに微分します。
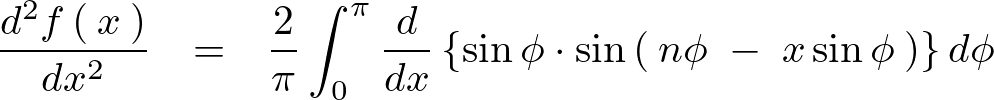
先程と同様に以下のように分けて微分してチェインさせます。


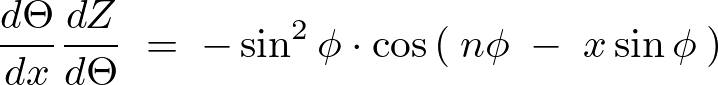
代入すれば、
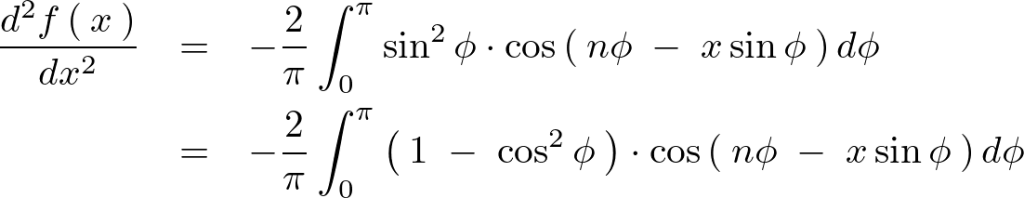
![]() の2階微分は以下のようになります。
の2階微分は以下のようになります。

ここでいったん先ほどの1階微分に戻ります。
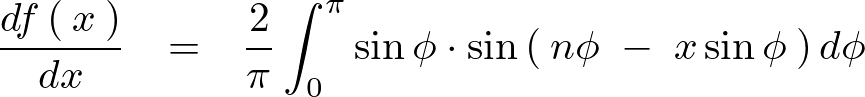
この式に対してはここで![]() に対して積分を行います。このとき使用するのは部分積分になります。
に対して積分を行います。このとき使用するのは部分積分になります。
部分積分の公式は上記式の![]() に合わせて記述すれば以下のようなものでした。
に合わせて記述すれば以下のようなものでした。
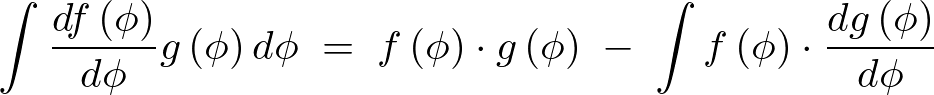
これを上記の一階微分後の積分式に対して![]() で部分積分をしていきます。
で部分積分をしていきます。

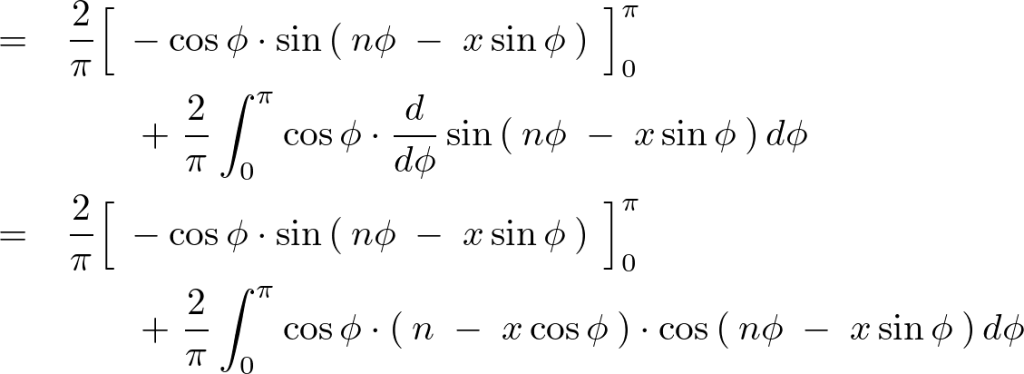
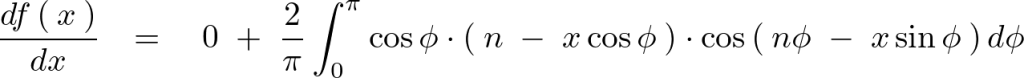
これにより![]() による一階微分の
による一階微分の![]() での部分積分に関しては次のようになります。
での部分積分に関しては次のようになります。

この式の両辺に対して次のように![]() を掛けます。
を掛けます。

さらに今度はフーリエ係数の2階微分の式に対して次のような形にして式を変形させます。
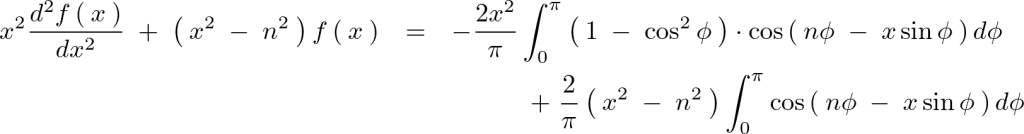

以下のような式が導かれます。
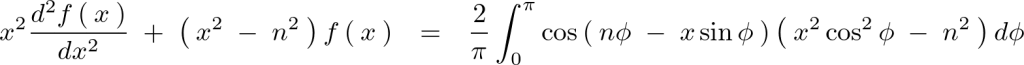
これらの式を以下のようにして辺々たし合わせます。
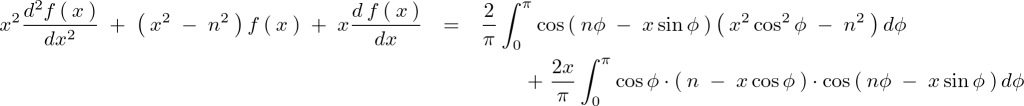

次のように求まります。
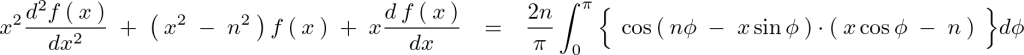
ここでいったん右辺の括弧のなかの式の微分積分に関しての逆算を考えます。
次のような式、
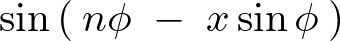
これを![]() で次のように微分します。
で次のように微分します。


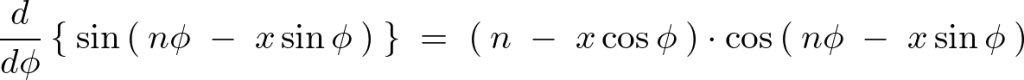

であると考えて右辺の積分式に代入します。

となるので以下のような微分方程式が導かれます。
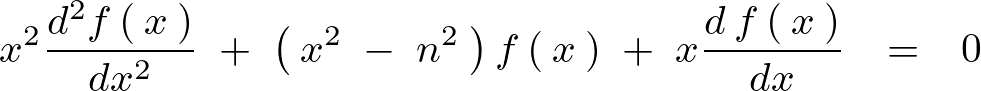
これを整理すれば、

これがケプラーの方程式から求められるベッセルの微分方程式と呼ばれるものになります。
参考書籍
特殊関数とその応用POD版 (著):薮下 信
このカテゴリーではこうした基本事項をふまえながら以下のようなベッセル関数の様々な考察を行っていきます。

ベッセルとガンマ関数
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

円形膜の振動
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.