偏微分方程式とは
線形偏微分方程式
2つ以上の独立変数とその偏導関数を含む微分方程式のことを偏微分方程式といいます。![]() 階とはその編微分方程式において含まれている最も高い値(最大の作用素)の階数に合わせて
階とはその編微分方程式において含まれている最も高い値(最大の作用素)の階数に合わせて![]() 階偏微分方程式という言い方をし、このとき変数が2変数の場合
階偏微分方程式という言い方をし、このとき変数が2変数の場合![]() 、
、![]() についての係数をそれぞれ
についての係数をそれぞれ![]() 、
、![]() 、
、![]() 、そして未知関数を
、そして未知関数を![]() 、既知の関数として
、既知の関数として![]() を定義すれば、2階の偏微分方程式は、
を定義すれば、2階の偏微分方程式は、
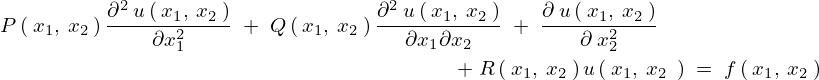
また、上記の式は常微分方程式のときと同様に偏微分方程式内における未知関数![]() とその導関数、
とその導関数、
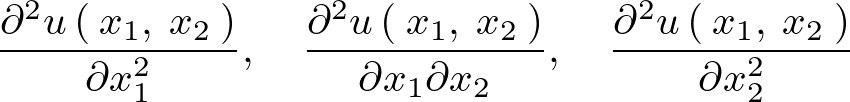
に関して一次式であれば線形であるということを意味します。
通念的に![]() 解の偏微分方程式における一般解とは
解の偏微分方程式における一般解とは![]() 個の任意関数を含む解のことをいいます。これが常微分方程式の場合と違うところになります。
個の任意関数を含む解のことをいいます。これが常微分方程式の場合と違うところになります。
また上記偏微分式の既知の関数![]() のときを同次、それ以外(
のときを同次、それ以外(![]() のときを非同次といいます。
のときを非同次といいます。
2階線形偏微分方程式の一例
2階線形偏微分方程式の重要なものとしては以下のようなものがあります。

それぞれの偏微分方程式の特徴
双曲型偏微分方程式
- 波動方程式 変数として時間変数
- 移流方程式 速度場の下で保存スカラー量を記述する
放物型偏微分方程式
- 拡散方程式(熱伝導方程式) 変数として時間変数を用いて与えられている領域内において時間とともに変化する物体の場を記述し以下の式で与えられる
楕円型偏微分方程式
- ラプラス方程式 重力場や静電場ポテンシャルを記述しその解理論はポテンシャル論といい、
- ポアソン方程式 ラプラス方程式の一般化による
- ヘルムホルツ方程式 電磁波放射など、次の方程式によって与えられる
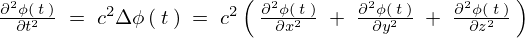
 の解では調和関数を与える
の解では調和関数を与える
境界値問題とは
一般的に無数の解を持つ微分方程式においてその定義されている領域の境界上で解、またはそれの導関数の値に対し何らかの条件を課すことによって解を指定します。この条件を境界条件と呼び、この境界条件を満たす解を求める問題を境界値問題といいます。
またさらにほかの場合においては、例えば時間 が一つの変数として与えられている場合、あらかじめ定められている条件 ━ ある一定の初期条件によって決定される解を求める場合のものもあります。
が一つの変数として与えられている場合、あらかじめ定められている条件 ━ ある一定の初期条件によって決定される解を求める場合のものもあります。
解の重ね合わせ
同次型線形偏微分方程式において、ある領域内において関数![]() 、
、![]() が同時線形偏微分方程式の解ならば、
が同時線形偏微分方程式の解ならば、
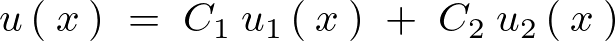
もまたその領域内においてその方程式の解となりえます。
ラプラス方程式
それぞれの座標![]() とした3次元座標空間において2階の偏微分作用素を
とした3次元座標空間において2階の偏微分作用素を![]() とし、この作用素を次のようにおきます。
とし、この作用素を次のようにおきます。
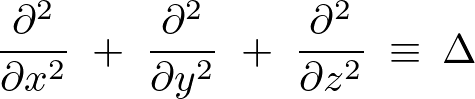
ここでナブラと呼ばれる次のもの、
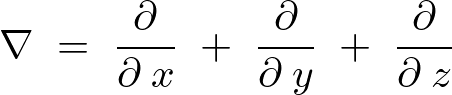
これを使って表せば上記式の2階偏微分作用素式の右辺![]() は次のようなものになります。
は次のようなものになります。
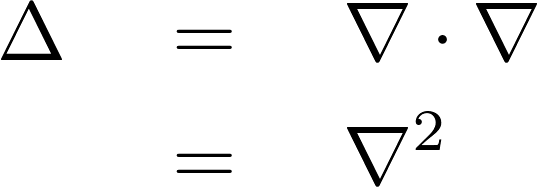
時間に依存しないある座標系における![]() を変数とする関数を
を変数とする関数を![]() とおくとラプラス方程式は以下のようになります。
とおくとラプラス方程式は以下のようになります。
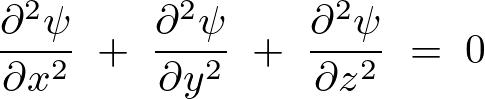
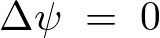

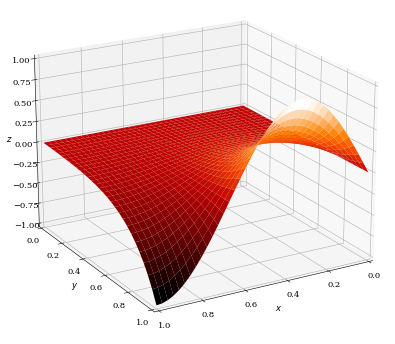
境界条件を課したある領域内において![]() なる条件を満たす解をラプラス方程式によって求めることができ、さまざまな解析を導くことが可能になります。
なる条件を満たす解をラプラス方程式によって求めることができ、さまざまな解析を導くことが可能になります。
これにより、物体の温度分布などの状態を記述するのに重要な役割をします。
1階偏微分方程式
未知関数を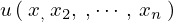 とした場合これに対する一般的な1階偏微分方程式は次の形に書かれます。
とした場合これに対する一般的な1階偏微分方程式は次の形に書かれます。
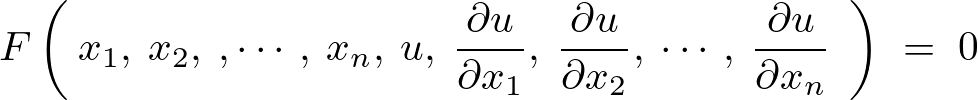
この解を考える上で、1階偏微分方程式を、
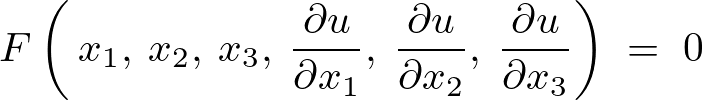
としたときその中に含まれる独立な任意定数![]() 、
、![]() 、
、![]() と置くと、
と置くと、
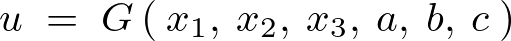
となるような解を完全解といいます。
例題
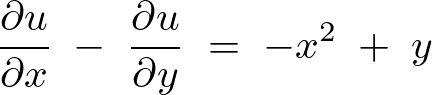
変数分離を行ってそれぞれ定数を![]() とおきます。
とおきます。
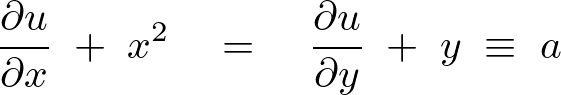
まず![]() より、
より、
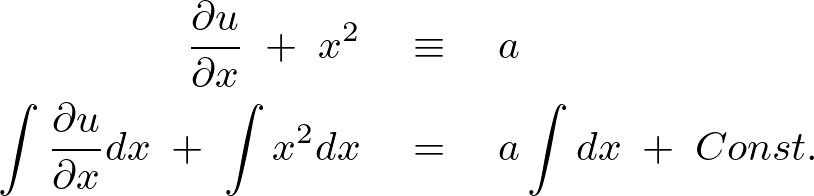

次に![]() に関して、
に関して、

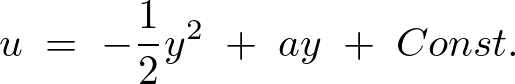
これにより解は、
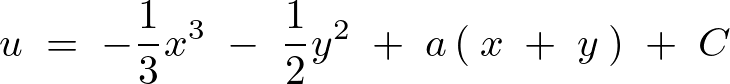
以上に挙げたものが偏微分方程式に関する簡単な一通りのものになります。このカテゴリでは境界値に関する問題、ラプラス方程式、その他1階偏微分方程式、定数係数偏微分方程式など、順次取り上げていく予定になっています。
以下のリンクより目的のコンテンツへお進みください。

Wait a moment
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Wait a moment
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.