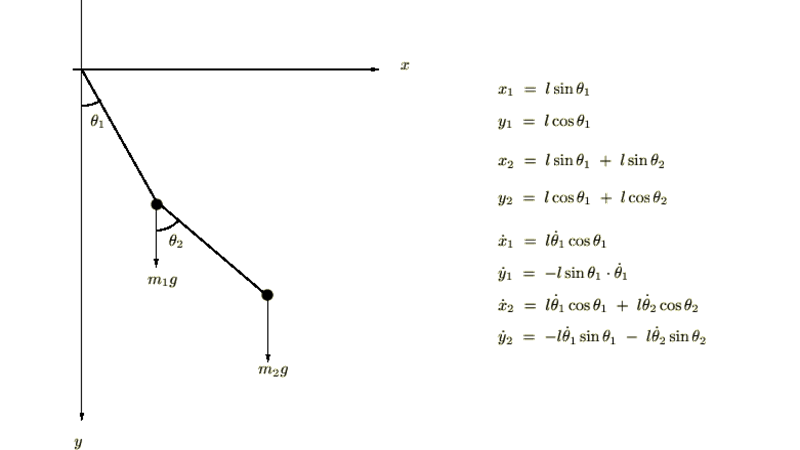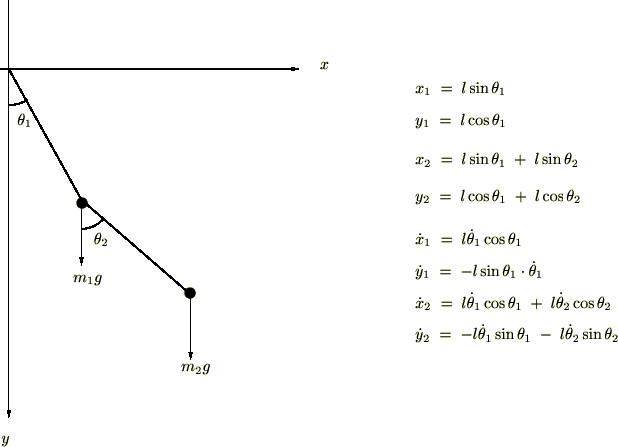ラグランジュ関数

速度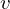で運動している質量の運動エネルギー

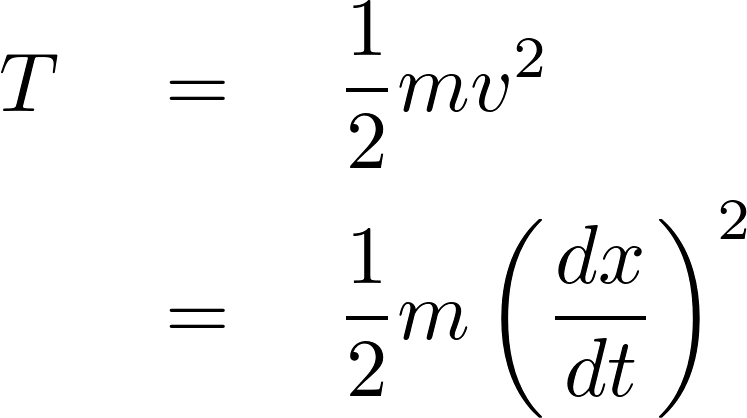
これの変分を考えてみましょう。簡単のために運動は軸方向のみを考え、そのずれの時間をからとします。

まず、自体の時間に対する変分と微分の関係を求めます。

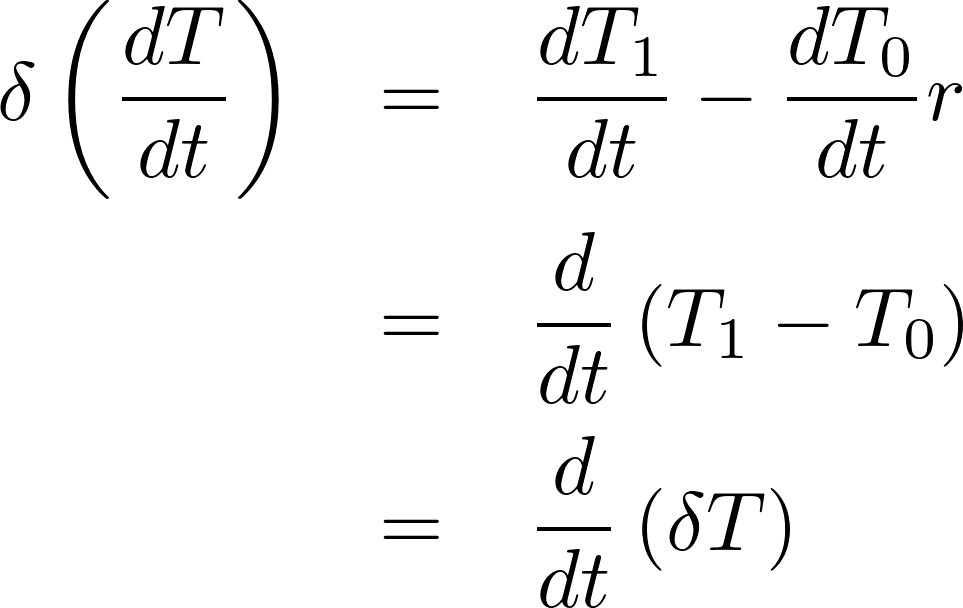
さらに運動エネルギーの変分を考えれば、

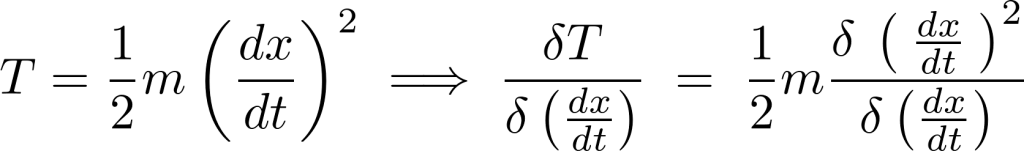
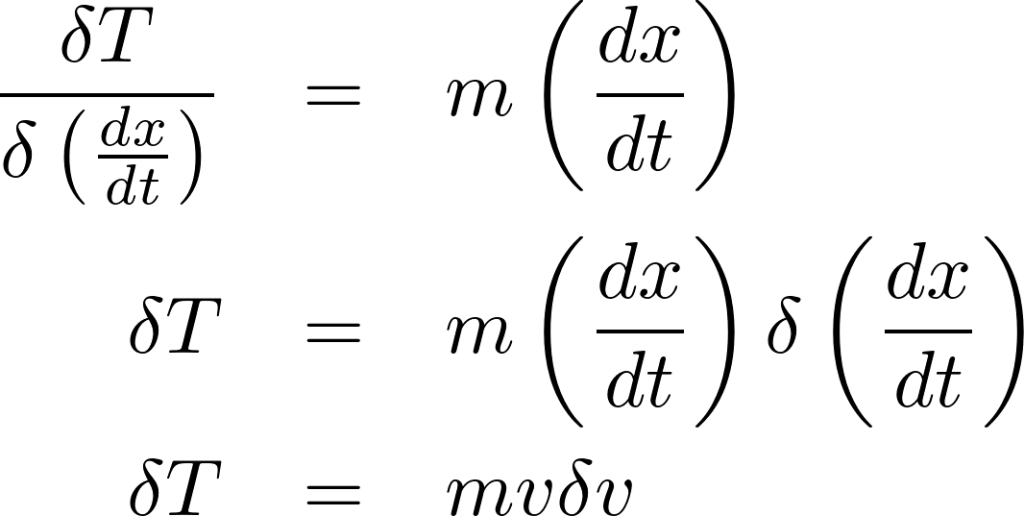
この出てきた上記の式に関して両辺をで積分します。

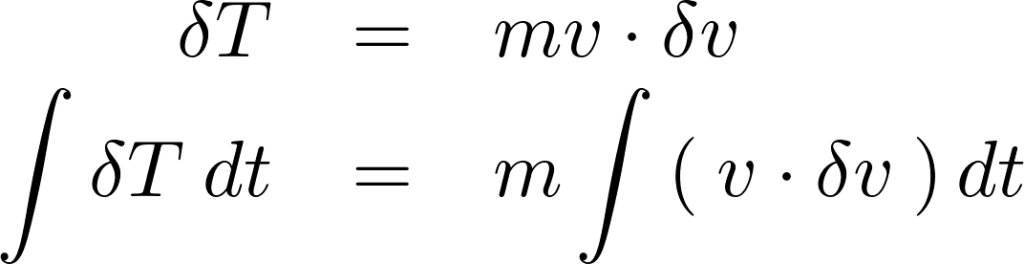
さらに上記積分式の右辺のののみ以下のように微分表記にします。

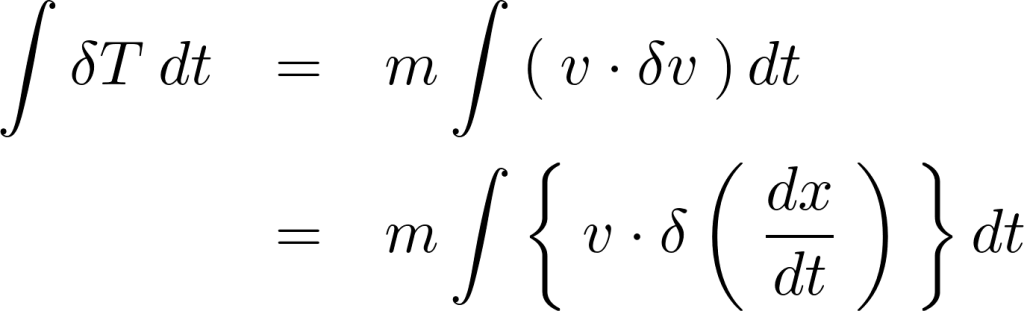
ここで微分と変分の入れ替えが可能なので次のようになります。

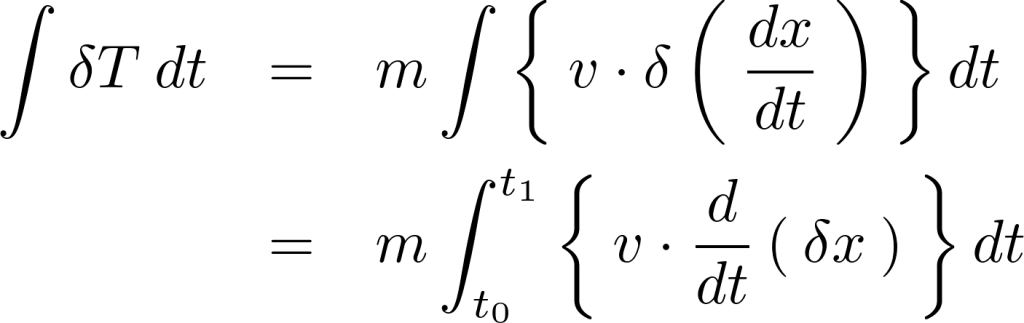
上記式の右辺に対してさらに部分積分を適用しますが、この時右辺の積分に関しては端点を固定しているので結果になることに注意すれば以下のようになります。

となるので次のように求まります。

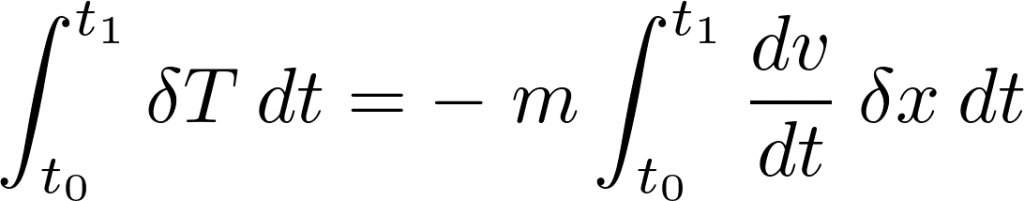
力がポテンシャルエネルギーなどの保存力だった場合は、

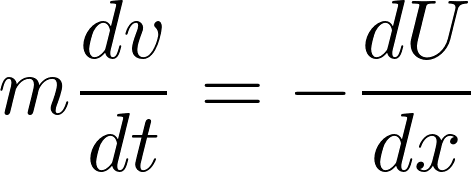
そしてこれの変分を考えれば、

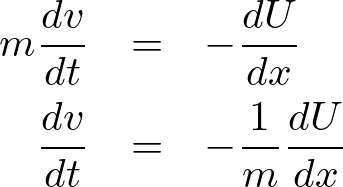
これを部分積分の結果に代入します。

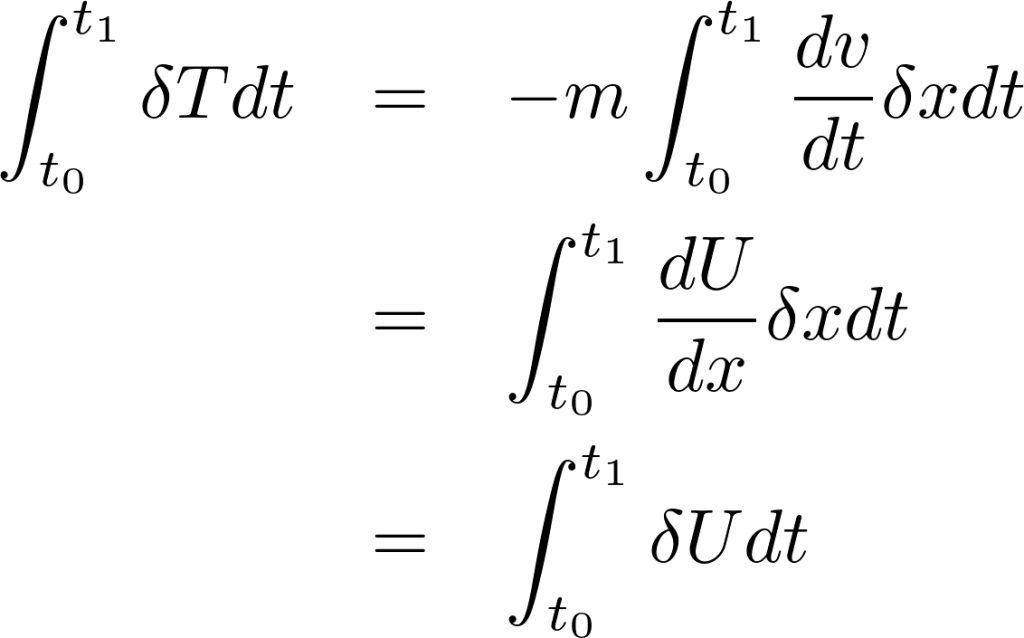
途中微分と変分を入れ替えています。

さらに以下のように式変形をしていきます。

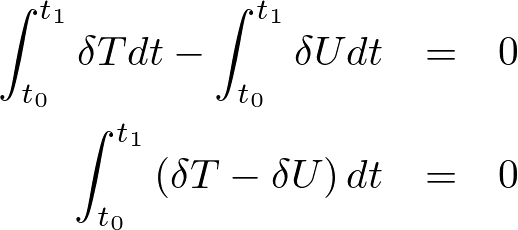
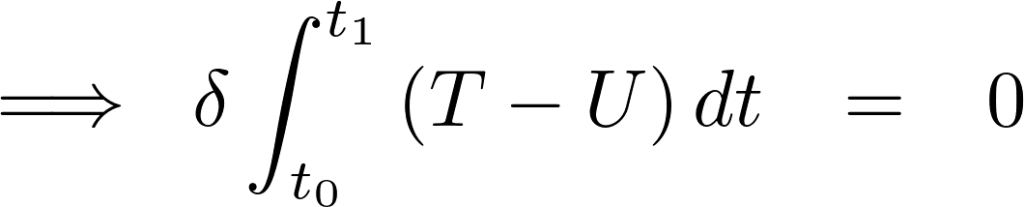
このように停留値をとらせるようなものになっており、実現される運動はこれを満たすものだと考えることが出来ます。

ここでこのをとおき、オイラーの方程式と対応させれば、

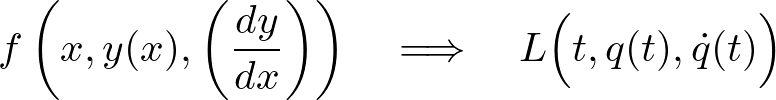
これより以下のような式が決まります。

これをに拡張すれば、

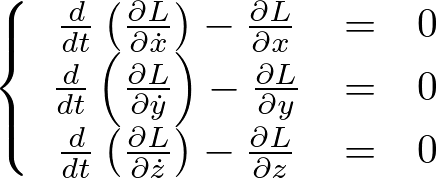
またさらにここでをと表せば、

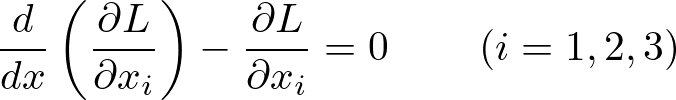
一般化運動量は、

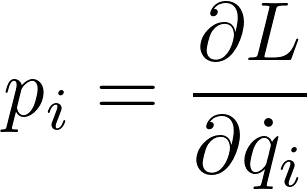
ある質点の運動

ある質点の運動を考えてみましょう。

を水平面としを鉛直上向きに座標を取ります。

そうするとラグランジアンは、

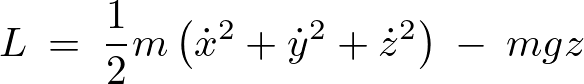
となるのでこれをラグランジュの式に当てはめれば、

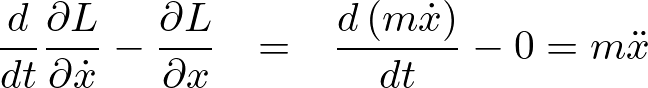
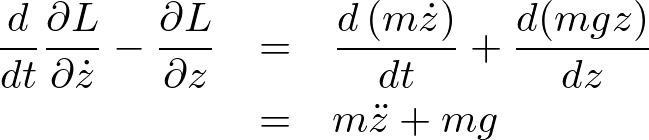
となるので結果は次のようになります。

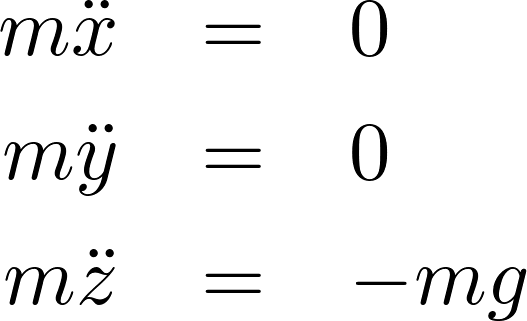
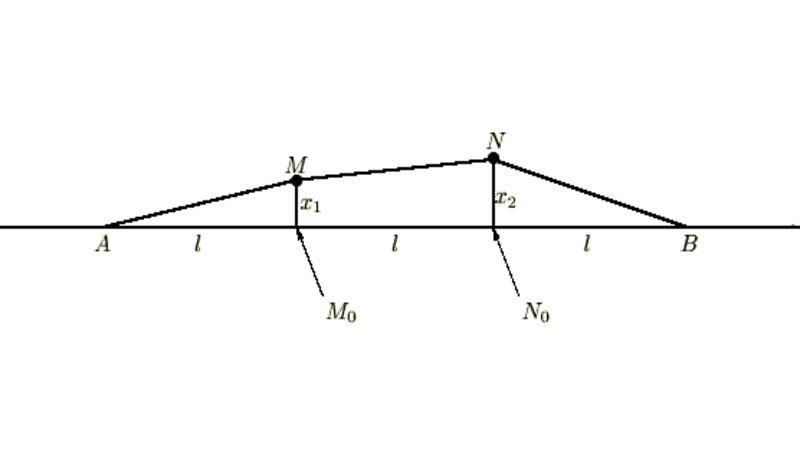
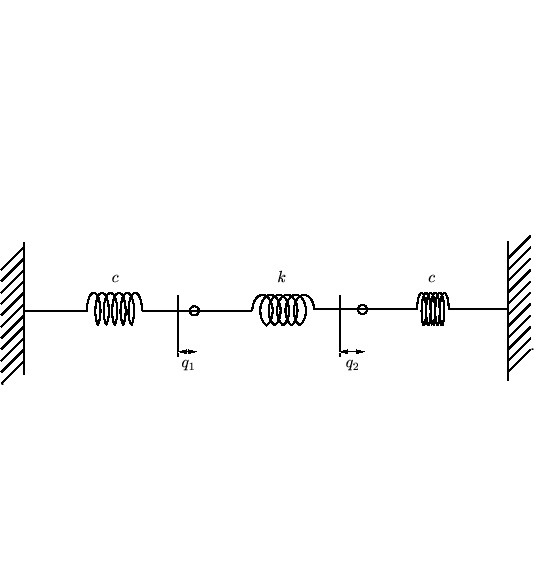
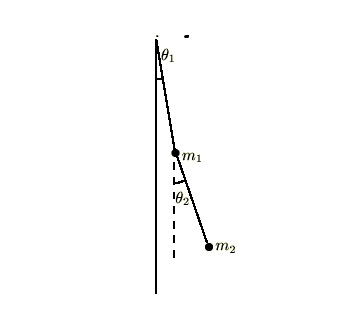
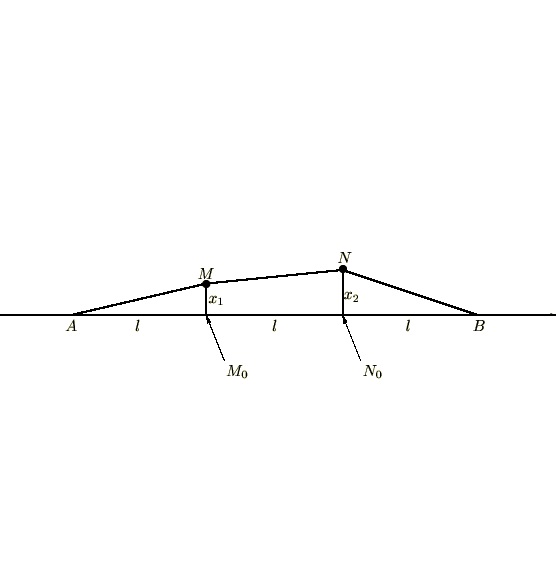
このカテゴリーではラグランジュ関数を使った弦及び3重ばねの連成振動、2重振り子の微小な場合とそうでない場合の考察を行っていきます。