ラプラス変換とは
今、時間に関する関数を、
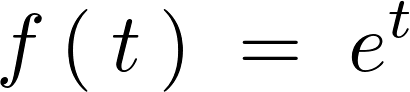
と置いたとします。
ある関数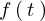 に対して
に対して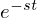 をかけてそれを
をかけてそれを からプラスの無限大
からプラスの無限大![]() の範囲において積分し、その積分によって
の範囲において積分し、その積分によって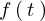 とは違う関数に変換することをラプラス変換するといいます。
とは違う関数に変換することをラプラス変換するといいます。
フーリエ変換コンテンツでも言ったように時間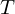 の世界で表現されていた関数を複素数の
の世界で表現されていた関数を複素数の![]() の世界の関数に置き換えることにより、通常では簡単には解けないような複雑な微分方程式を、このラプラス変換を行うことによって見通し(計算を簡素化)をよくするといった利点があります。
の世界の関数に置き換えることにより、通常では簡単には解けないような複雑な微分方程式を、このラプラス変換を行うことによって見通し(計算を簡素化)をよくするといった利点があります。
ラプラス変換の定義
今、考えている領域を とし、その関数
とし、その関数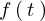 に対しての複素数を
に対しての複素数を![]() とした場合、
とした場合、
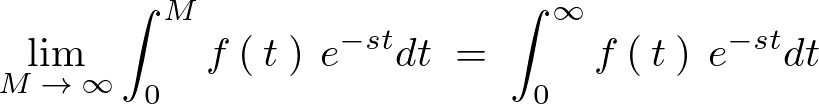
のような無限積分式が成立するとき、関数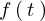 のラプラス変換といいます。
のラプラス変換といいます。
実際の計算
次のように考えます。
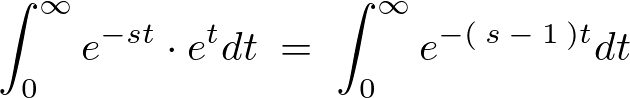
ここで上記式中の乗数部分を次のように置きます。
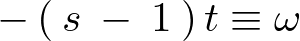
これを![]() で微分すると、
で微分すると、
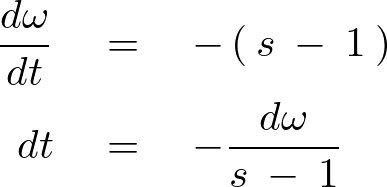
このように置換して以下のように計算していきます。

よって以下のように式変形できることになります。
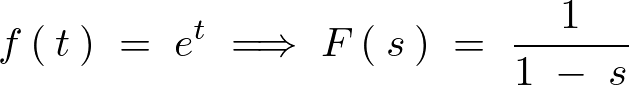
といった変数![]() の関数に変換されます。このような変換を行うことにより、ある微分方程式が代数的な計算によって解を導くことが可能になります。
の関数に変換されます。このような変換を行うことにより、ある微分方程式が代数的な計算によって解を導くことが可能になります。
フーリエ変換に関しては以下のように表現しています。
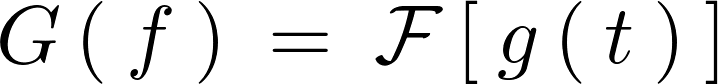
ラプラス変換に関しても踏襲して一般的に次のような表現をします。
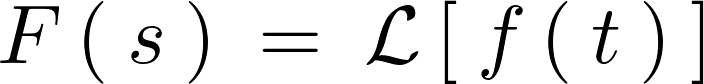
ラプラス変換公式とその証明
時間関数のラプラス変換
定数時間関数の場合
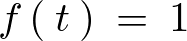 の場合のラプラス変換
の場合のラプラス変換
公式より、
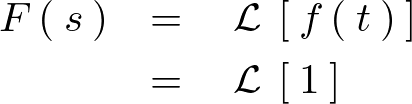
であるので以下のようにして積分計算していきます。
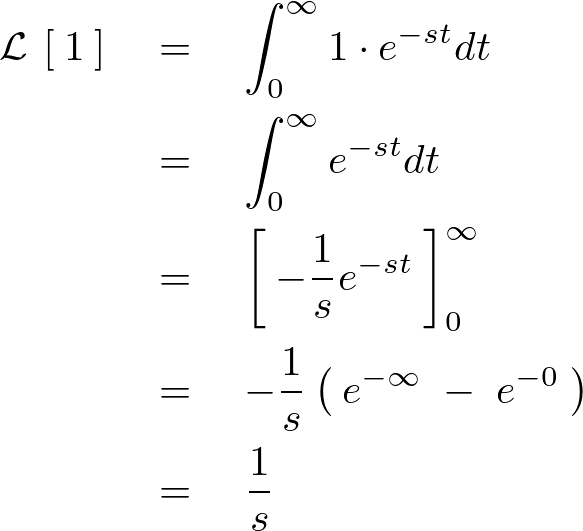
これより時間関数が定数の場合の結果は次のような式に変換されます。
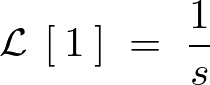
定数以外のラプラス変換
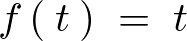 の場合のラプラス変換
の場合のラプラス変換
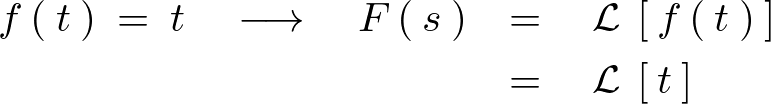
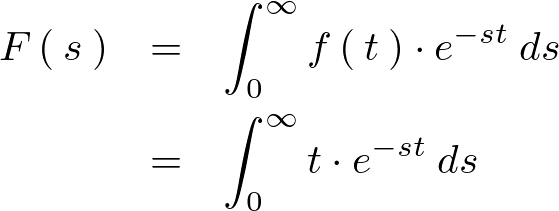
ここで部分積分の公式、
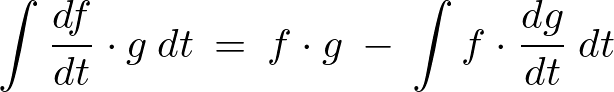
これより、
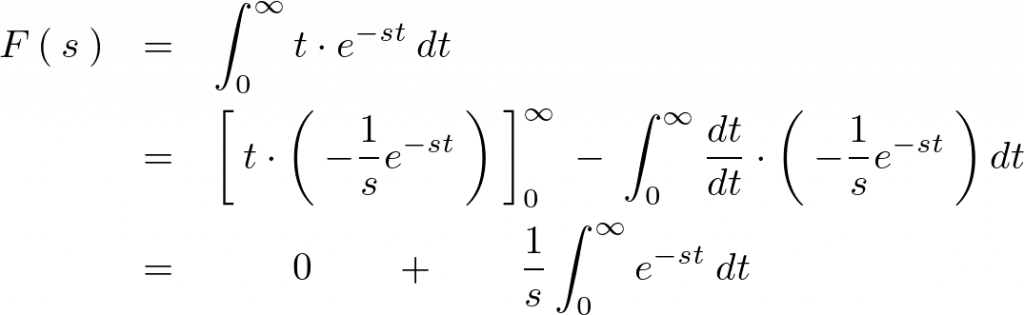
次のようになります。
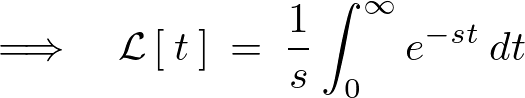
続けて積分計算していきます。
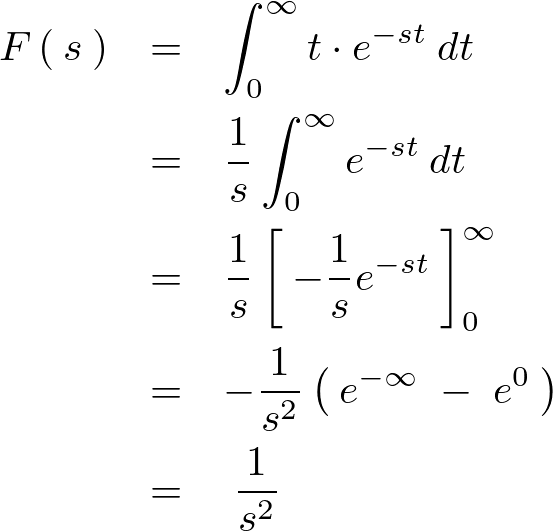
となるので時間![]() に関するラプラス変換は以下のようになります。
に関するラプラス変換は以下のようになります。
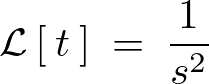
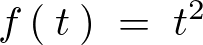 の場合のラプラス変換
の場合のラプラス変換
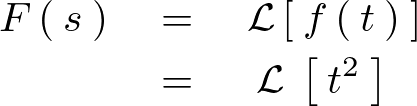
より先ほどと同様に積分計算していきます。
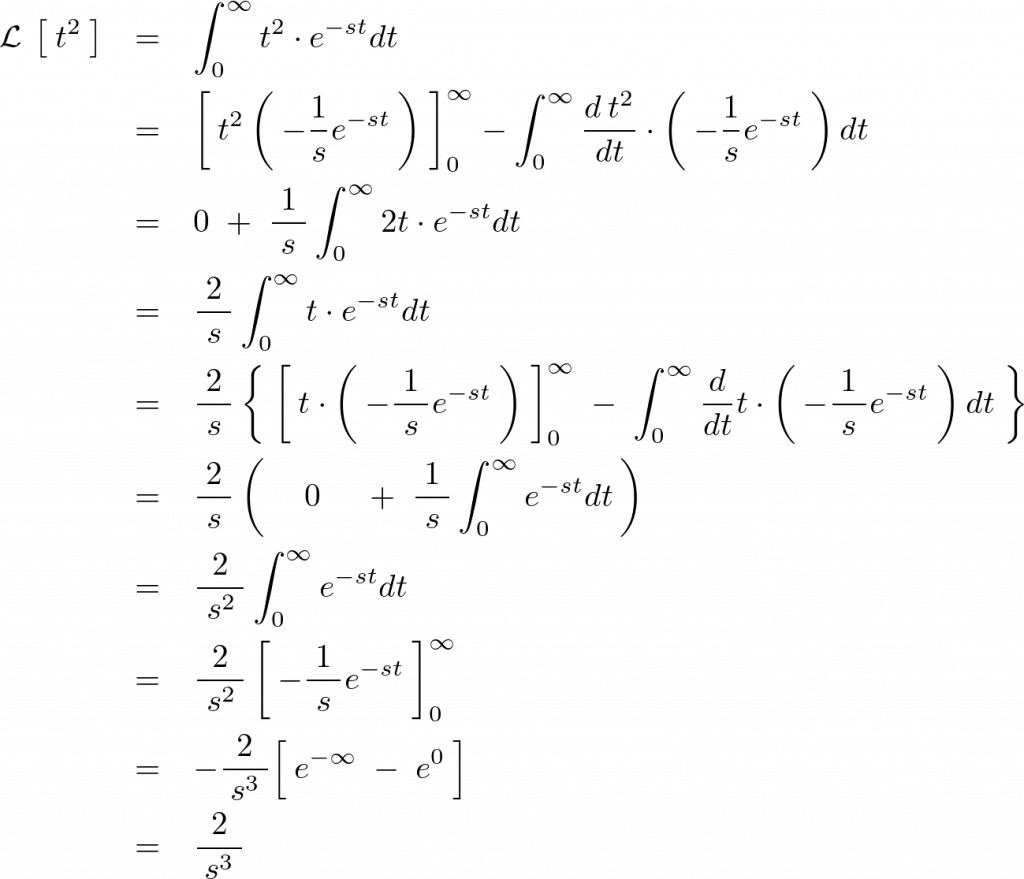
次のように求まります。
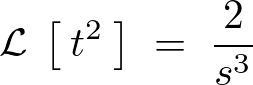
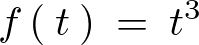 の場合のラプラス変換
の場合のラプラス変換
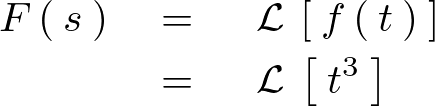
より、部分積分を使って計算していきます。
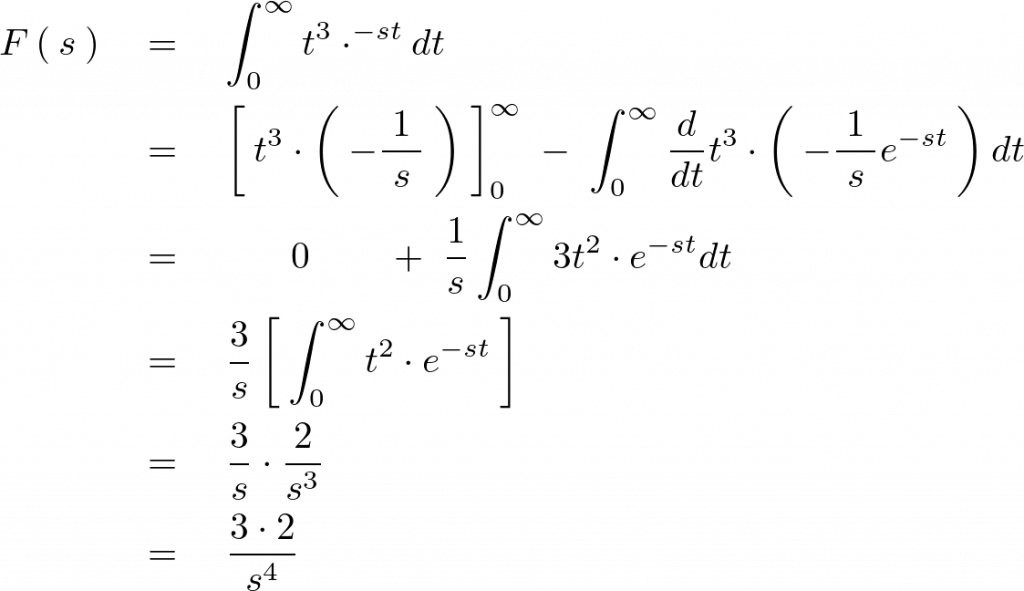
これより![]() の3乗のラプラス変換は次のようになります。
の3乗のラプラス変換は次のようになります。
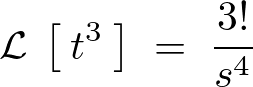
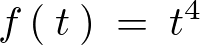 の場合のラプラス変換
の場合のラプラス変換
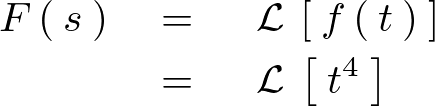
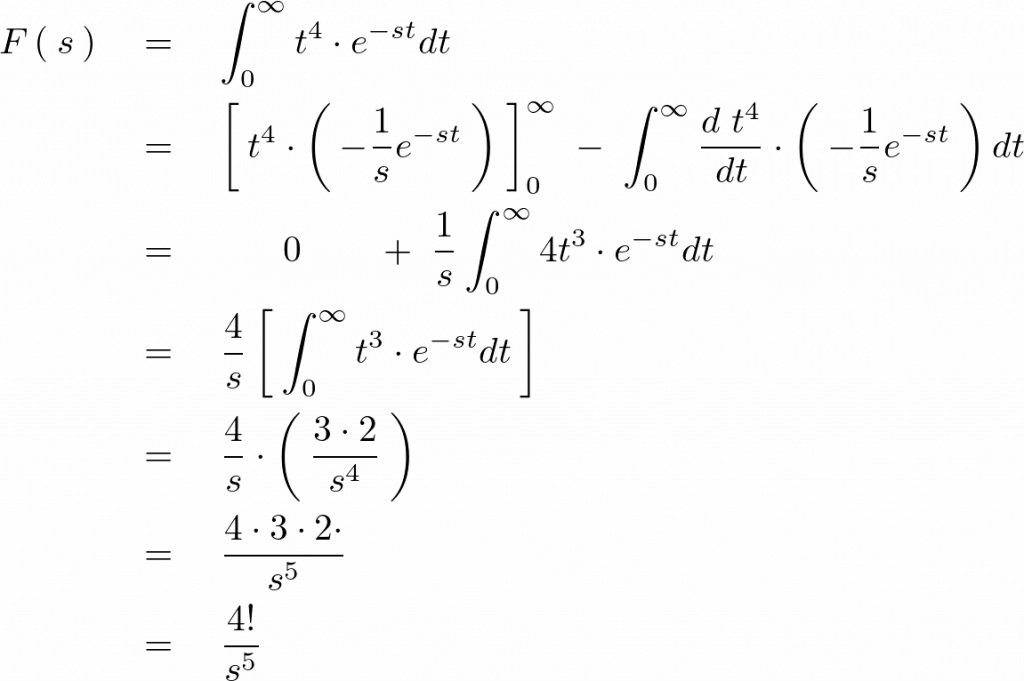
よって![]() のラプラス変換は次のように求まります。
のラプラス変換は次のように求まります。
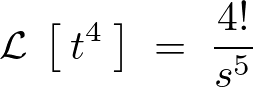
これらの結果をまとめると次のような公式が求められます。
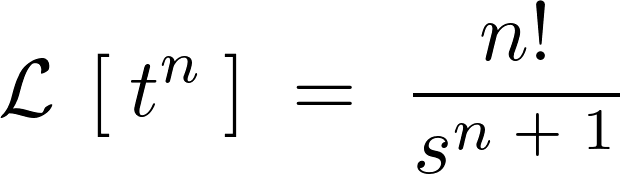

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
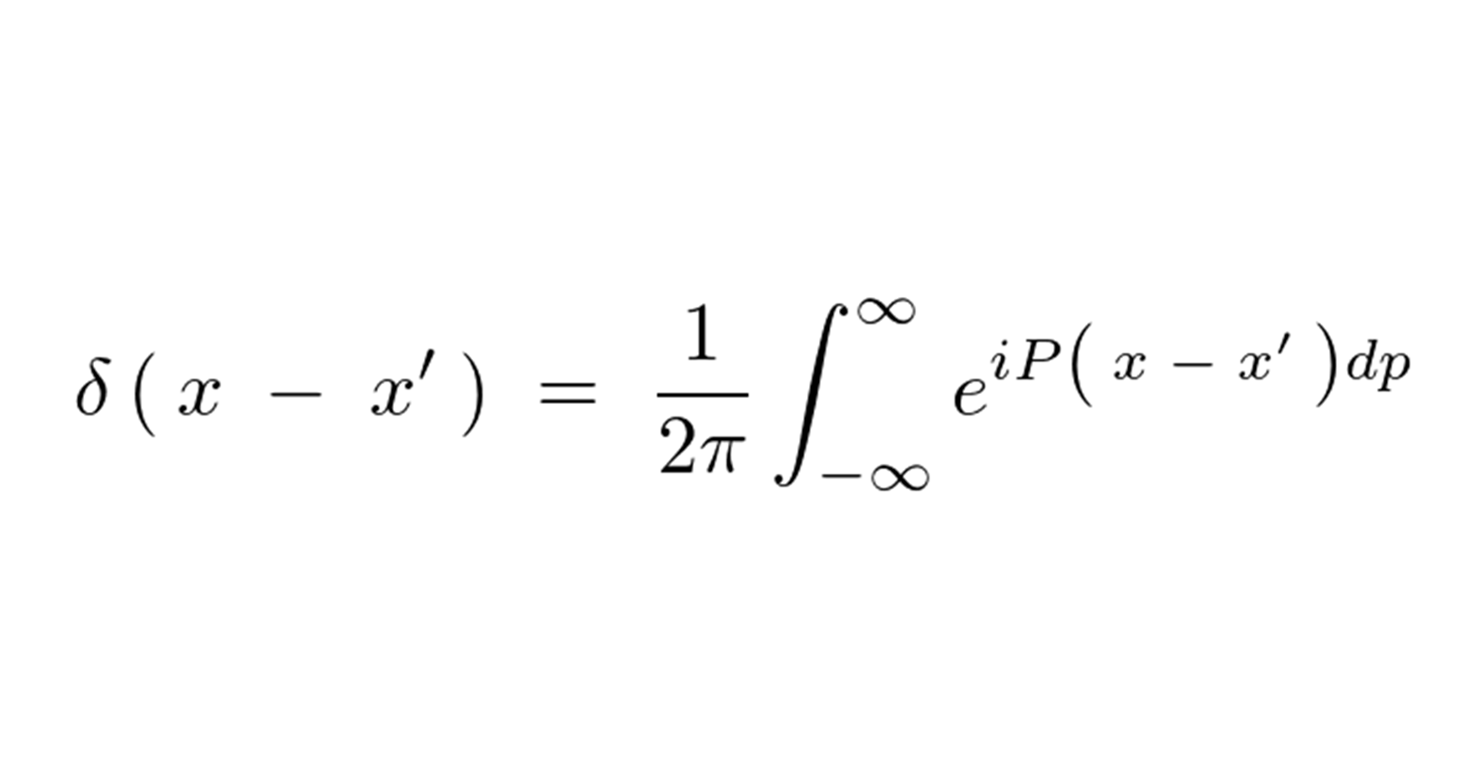
デルタ関数のフーリエ変換
カテゴリー
-
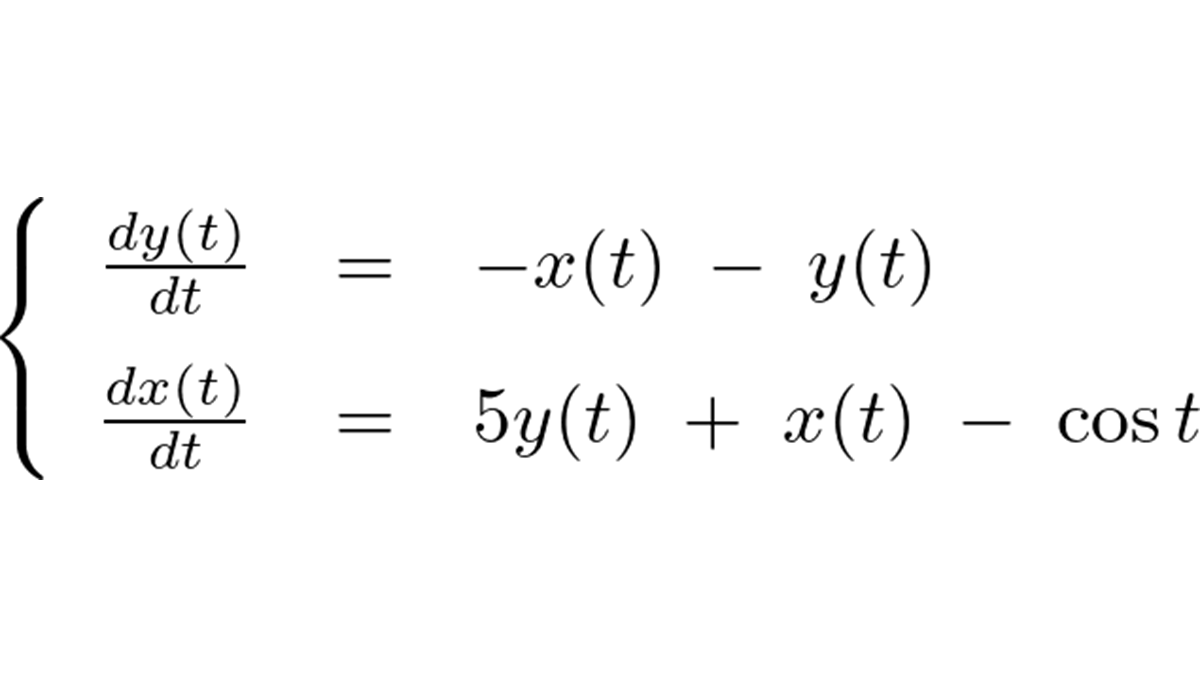
連立微分方程式の解法②
カテゴリー
-
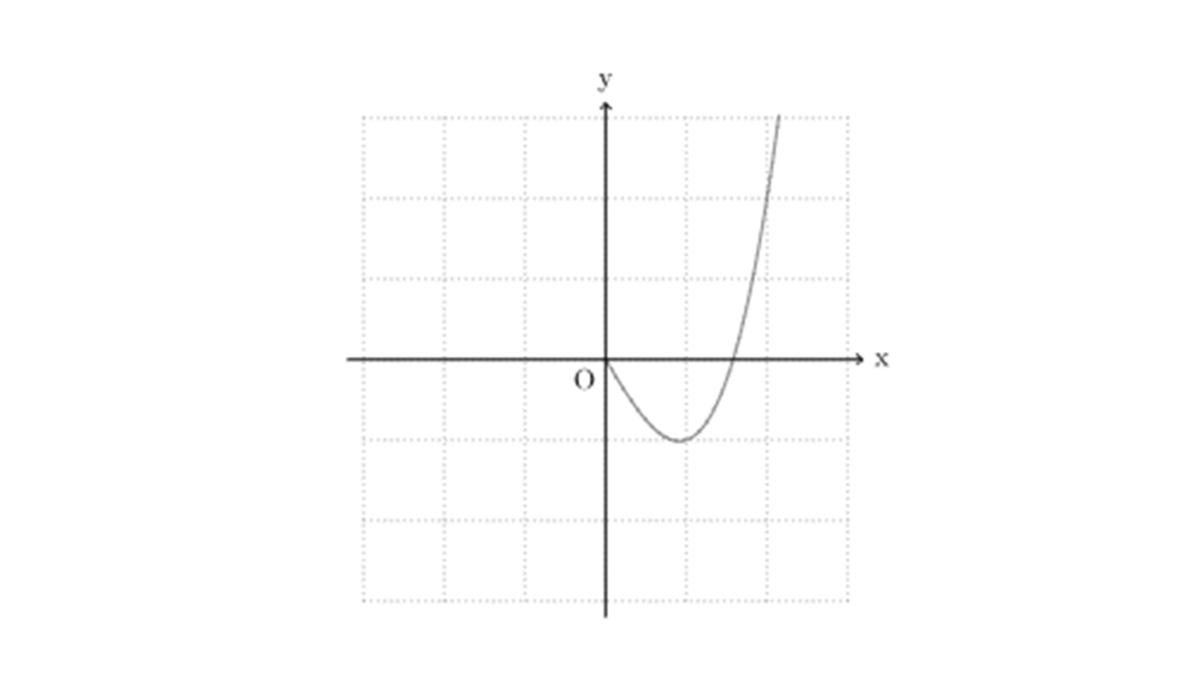
ヘヴィサイドの階段関数
カテゴリー
-
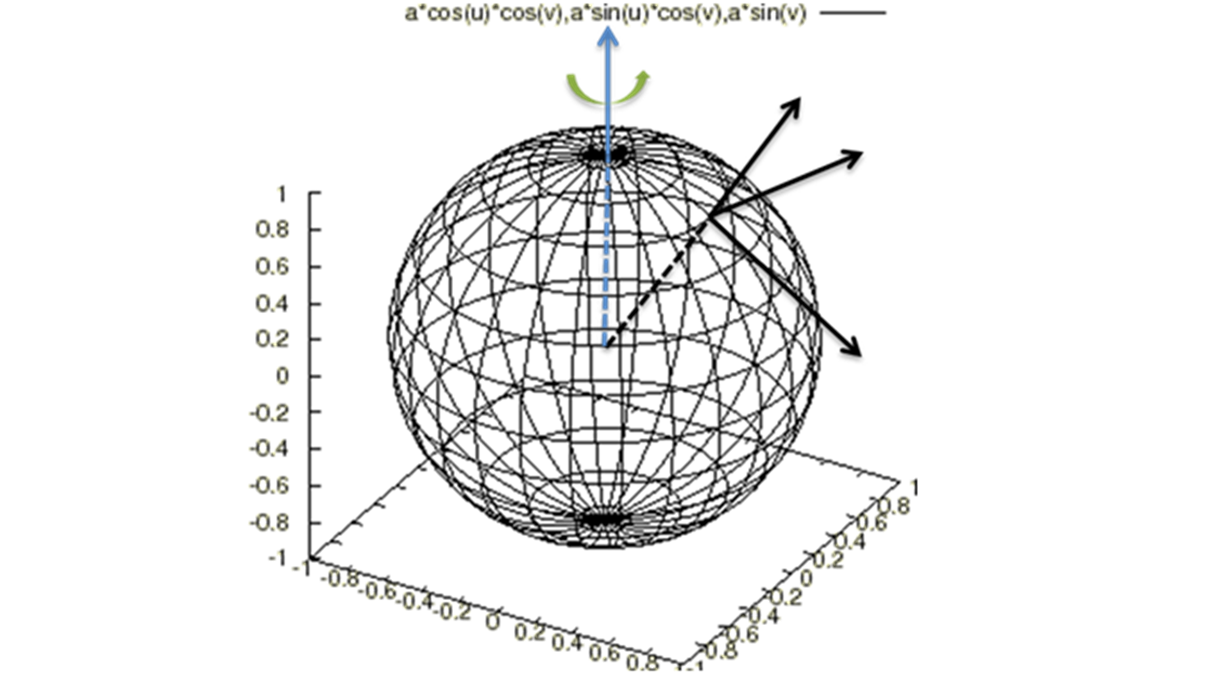
コリオリ弾道軌道計算③
カテゴリー
-

コリオリ弾道軌道計算②
カテゴリー
-

コリオリ弾道軌道計算①
カテゴリー
このチャプターではこのラプラス変換を主に取り扱っていく予定になっています。