波動方程式とは

２階の偏微分方程式における境界値問題

２階の偏微分方程式における境界値問題として、ここでは波動方程式を取り上げます。

波動方程式とは、波動の変位に関して時間と座標に関する変数を独立変数としてとらえることのできる定数係数型偏微分方程式（双曲線偏微分方程式）であり、この方程式における境界値に関する問題を、半区間におけるフーリエ積分表示などを使って解いていくことを考えていきます。

境界条件

境界条件としてまず次のように置きます。

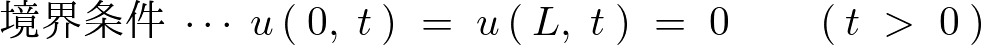
さらに弦の初期条件とその速度微分を次のように与えます。

ここで上記の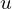を、距離と時間の２つの変数を含む次のようなもととします。

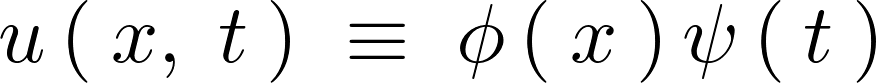
波動方程式に対してそれぞれ当てはめれば、

左辺

右辺

これらにより、

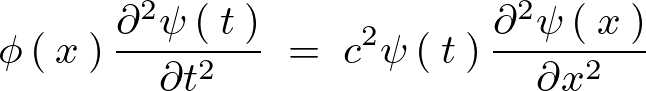
上記式に対して変数分離を行うと、

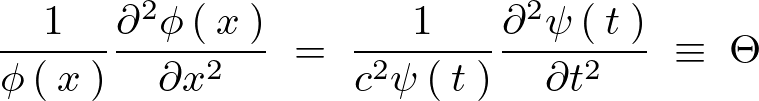
それぞれの変数に分離できたのでまずは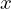のほうから考えていきます。

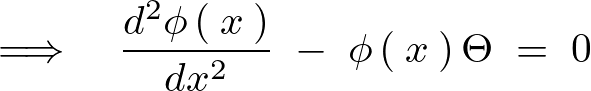
次のような条件を考えます。

といった条件を満たすものを求めます。

の解での式を満たすものは次の3種類が考えられます。

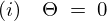のとき

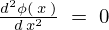という条件での一般解を求めます。

以下のように積分を実行していきます。

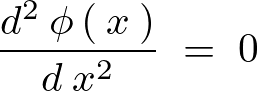
さらに積分を実行していきます。

よってのときの一般解は以下のように求まります。

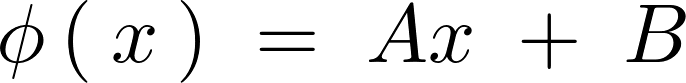
条件より、

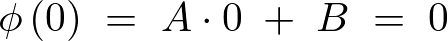
さらにの条件、

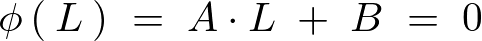
も考慮すればはとなり意味がありません。

のとき

一般解は、

となるので条件より、

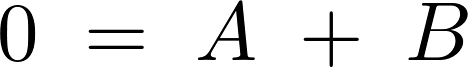
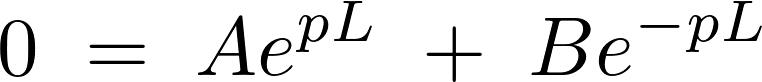
となります。

この場合も再びはとなるので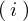と同じように解として意味がありません。

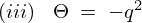のとき

最後のを実際にやってみると、

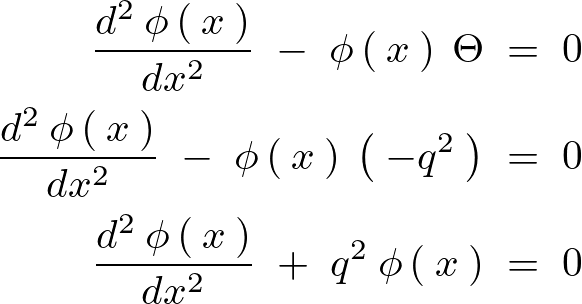
よって以下のように求まることになります。

このためこの式の特性方程式は以下のような複素数解になることになります。

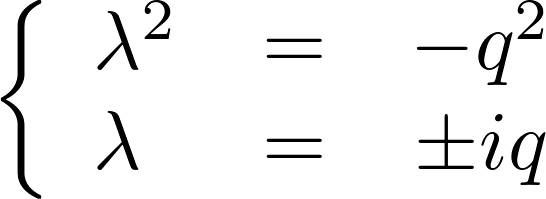
実数部は、虚数部はなので特性方程式は、

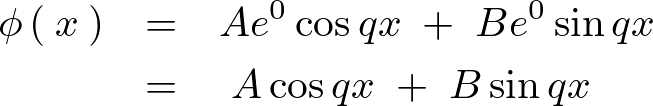
条件より、

なので、

ここでであるためには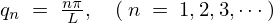という条件が必要になります。

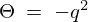の場合はの条件を満たすの解として、

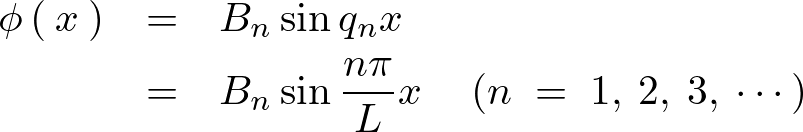
さらにに関して、

意味のある解を代入すれば、

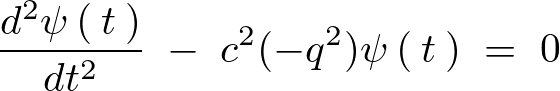
先ほどの結果を代入すると、

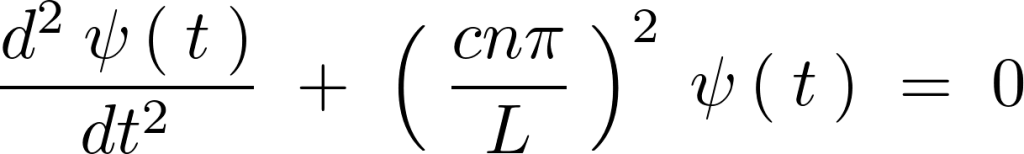
この方程式の解を求めるために同様にして特性方程式を導くと、

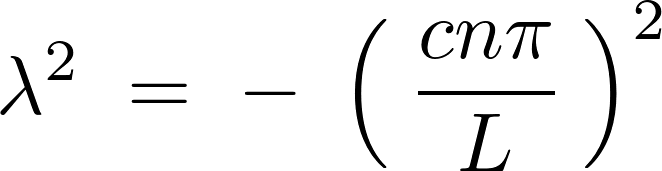
より、

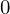実数部がで虚数部がなので、

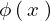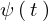これらの結果をそれぞれおよびとして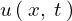に代入すれば、

ここで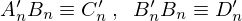と置けば、

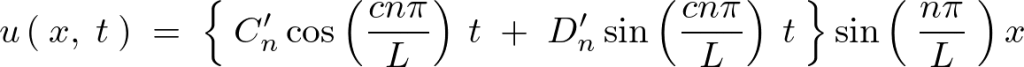
上記式中の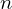は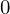を除く整数であり異なる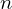に対してもまた同様にの解として成立します。

または線形微分方程式であり独立な解どうしであったとしてもそれらを重ね合わせたものもまた同様に線形微分方程式の解となります。

線形の重ね合わせの原理を考えれば、

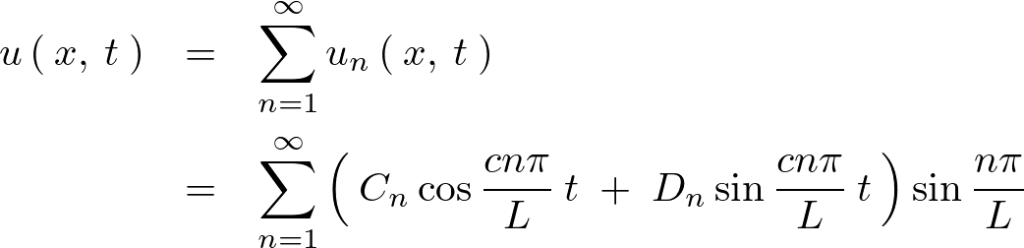
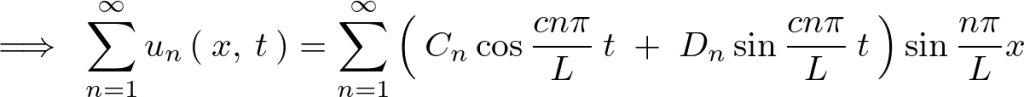
初期変位のときに、

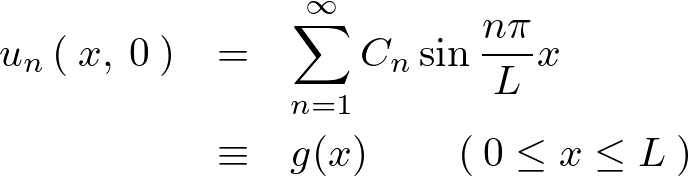
ここで式を見やすくするために次のように置きます。

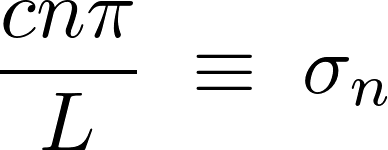
フーリエ級数の半区間の展開において奇関数での拡張を思い出せば、

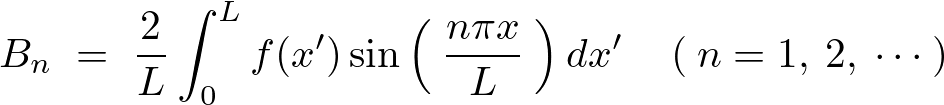
これを使えば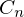、および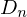は以下のように求まります。

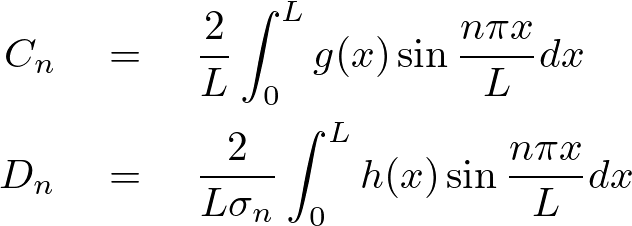
上記を代入すれば以下のような一次元波動方程式の解が求まります。