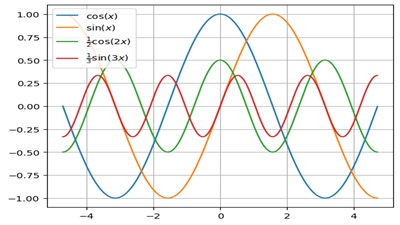
フーリエ級数展開
フーリエ級数展開とは
フーリエ級数展開とは、ある周期的な関数をコサインやサインなどの三角関数を使って関数の和の形に表したものになります。
このセクションではサインコサインそれぞれに付随する項に分けながら実際の簡単な周期関数に対してこのフーリエ級数展開を用いてそれらを表現していく方法に関して考察していきます。
フーリエ球数展開
区間![]() における積分可能な関数
における積分可能な関数![]() は次のように展開することが可能です。
は次のように展開することが可能です。
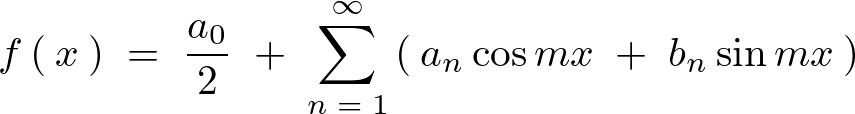
このように表現されるとき、上式の右辺において以下のように展開していった式、
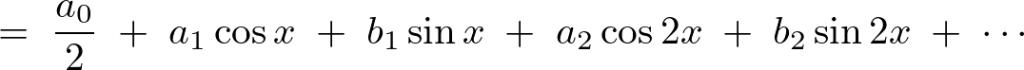
の部分をフーリエ級数展開といいます。
ここで上記式の![]() は次のようになります。
は次のようになります。
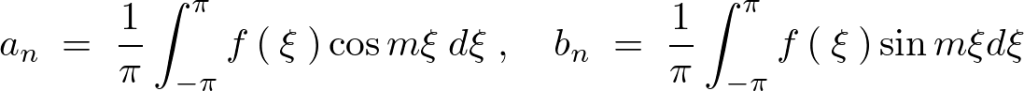
この![]()
を求めていきます。
まず、
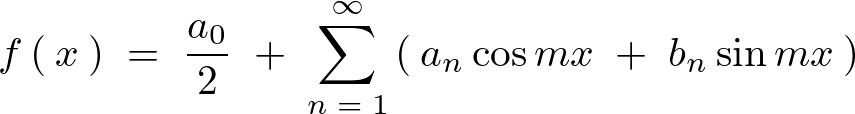
の両辺に![]() をかけます。
をかけます。
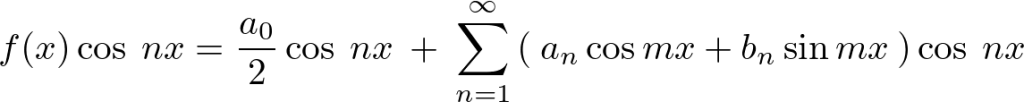
これを![]() から
から![]() までにかけて積分を実行します。
までにかけて積分を実行します。
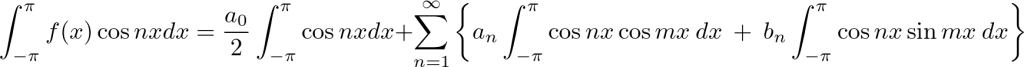
◆右辺第1項の計算
まず右辺第一項、
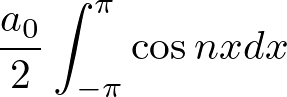
から計算していきます。
![]() なので
なので![]() 。
。
よって、
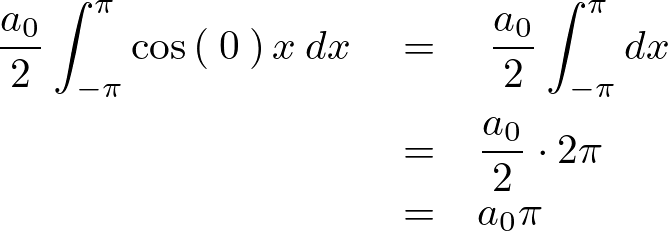
次に![]() の導出において三角関数の性質についておさらいします。
の導出において三角関数の性質についておさらいします。
三角関数の加法定理に関しては以下のような性質があります。
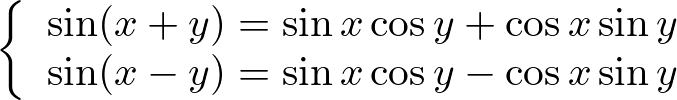
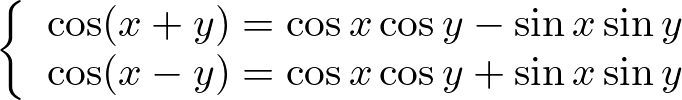
上記の式を覚えるコツは![]() はのほうは“シンコスコッシン”、
はのほうは“シンコスコッシン”、![]() のほうは“コスコスシンシン”、などとすると覚えやすいです。
のほうは“コスコスシンシン”、などとすると覚えやすいです。
そして![]() の場合は符号はそのままで、
の場合は符号はそのままで、![]() のほうは符号が逆になるということに注意します。
のほうは符号が逆になるということに注意します。
この式において、互いに引き算足し算などをするとさらに次のような式が示されます。

こういった性質を使って上記の積分を解いていきます。
◆右辺第2項の計算
まず![]() の場合、
の場合、
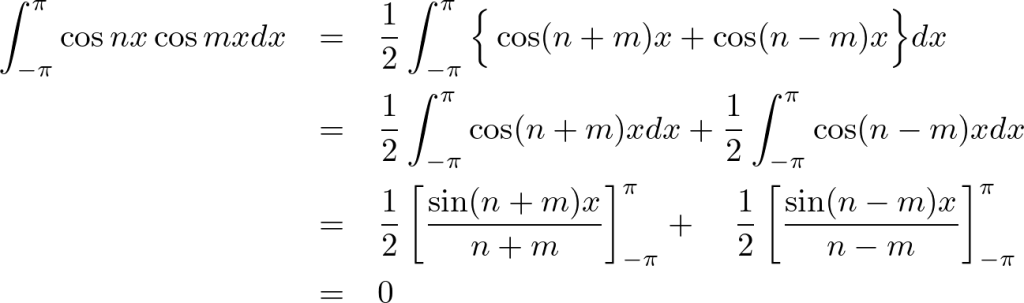
上記式においては三角関数の![]() 、
、![]() という関係を使っています。
という関係を使っています。
次に![]() である場合、
である場合、


この結果から、![]() の場合、
の場合、 は
は![]() のときだけ
のときだけ![]() でない結果が出ます。
でない結果が出ます。

より、

さらに![]() の部分は、コサインの偶奇性
の部分は、コサインの偶奇性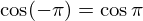 を使えば、
を使えば、

となり結果は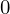 になります。
になります。
今度は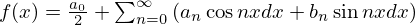 の両辺に
の両辺に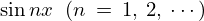 をかけてそれを
をかけてそれを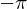 から
から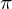 までにかけて積分を実行します。
までにかけて積分を実行します。
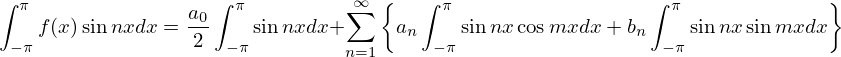
上記氏において右辺第1項は、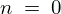 なので式自体が消去できます。
なので式自体が消去できます。
さらに第2項も上記のように計算していけば同様に結果は になります。
になります。
◆右辺第3項の計算
![]() のとき、
のとき、
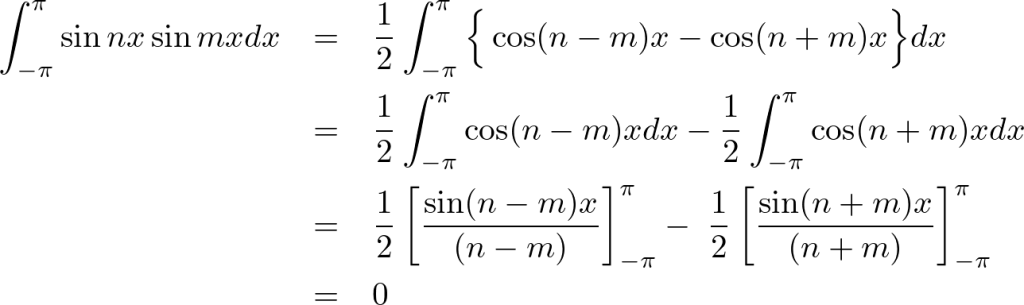
次に![]() のときは、
のときは、

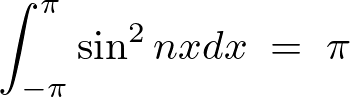
この結果により![]() のとき
のとき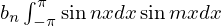 は
は![]() のときだけ
のときだけ![]() でない結果が出ます。
でない結果が出ます。
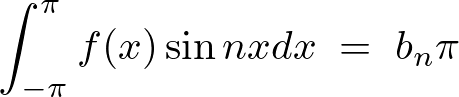
上記結果より、
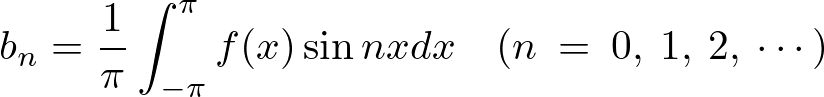
となりますが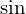 なので上記の
なので上記の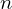 に関しては
に関しては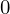 からではなく
からではなく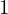 からになるので、
からになるので、
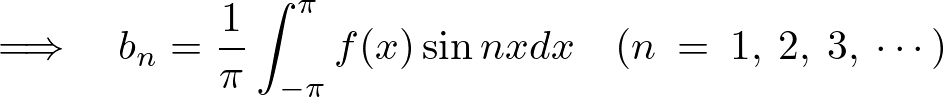
ここで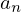 の展開において初項を考えます。
の展開において初項を考えます。
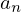 の項を展開していった場合は
の項を展開していった場合は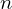 が
が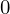 から始まります。
から始まります。
なのでその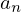 の展開した最初の
の展開した最初の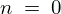 を書き出すと次のようになります。
を書き出すと次のようになります。
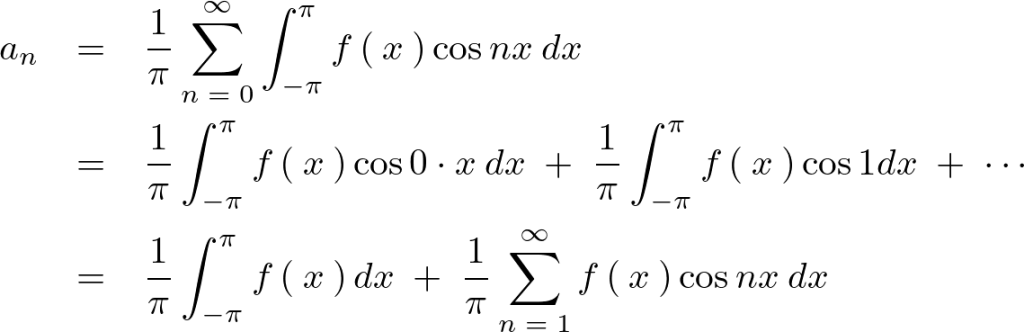
ここで に関しては、
に関しては、
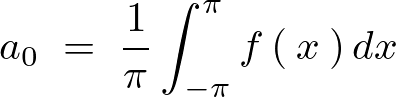
これを代入すれば、
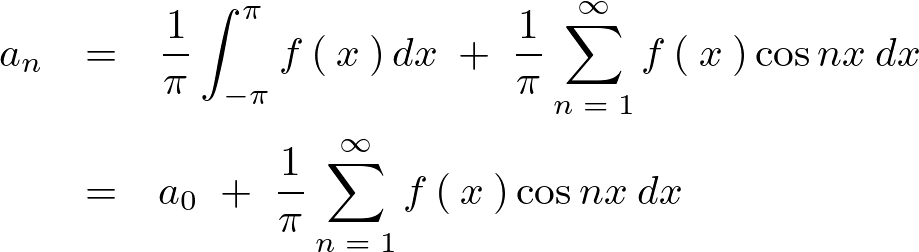
先ほどの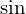 項の場合は和の記号がちょうど
項の場合は和の記号がちょうど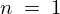 から始まるので
から始まるので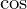 項と同じ和の記号を使えます。
項と同じ和の記号を使えます。
まとめれば、
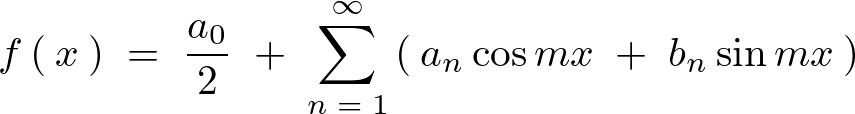
具体的な例
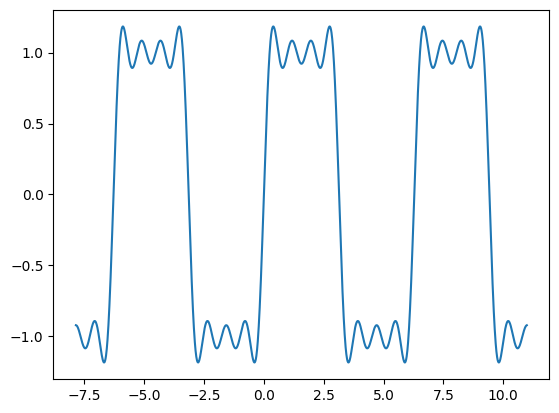
次に示す範囲の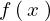 をフーリエ級数展開してみましょう。
をフーリエ級数展開してみましょう。
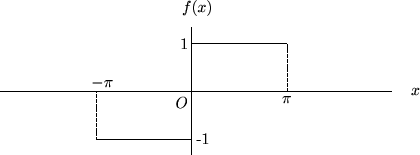
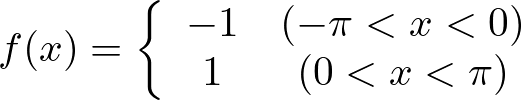
最初に を求めます。
を求めます。
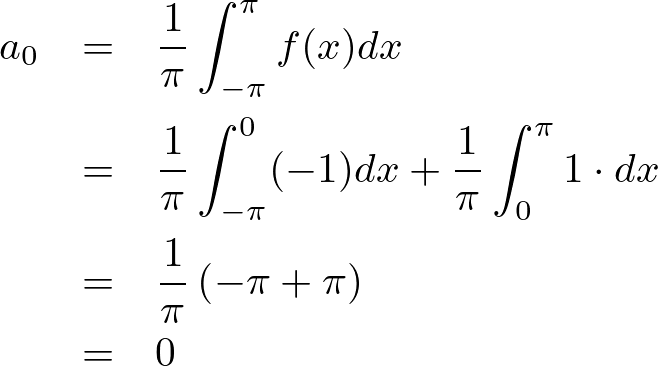
次に![]() を求めます。
を求めます。
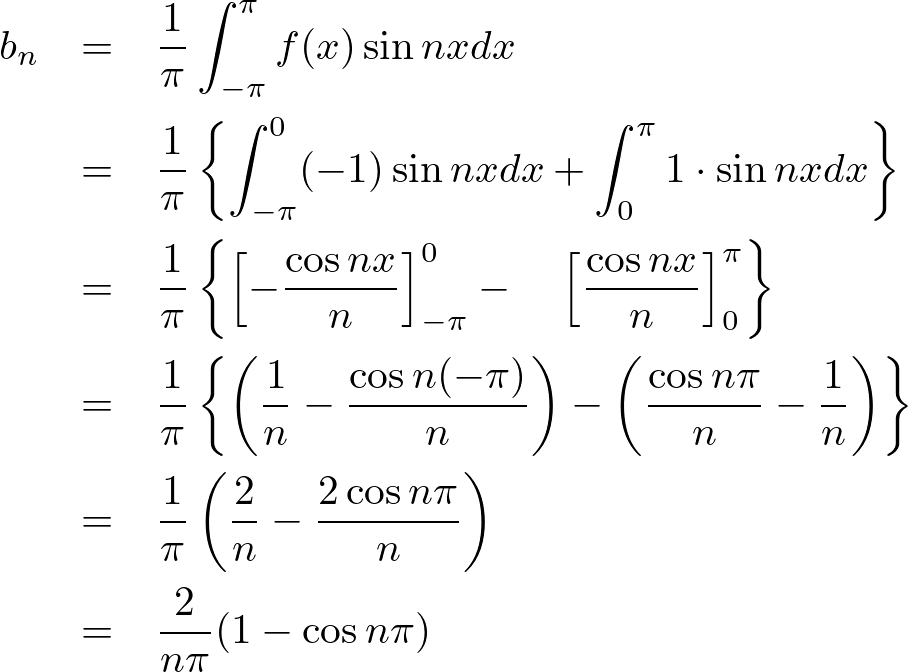
よって求める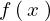 は、
は、
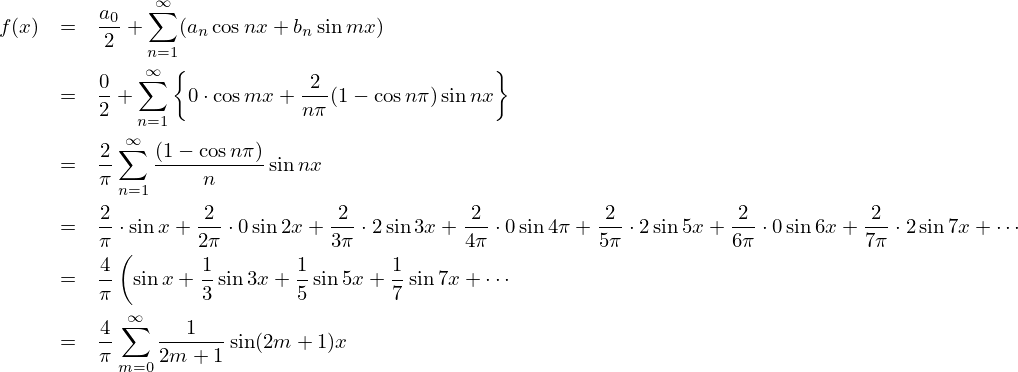
まとめれば、
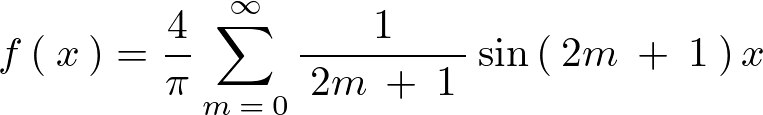

準備中
準備中

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.