境界値に関する問題

境界値問題 ━ 一般的に無数の解を持つ微分方程式においてその定義されている領域の境界上で解、またはそれの導関数の値に対し何らかの条件を課すことによって解を指定します。この条件を境界条件と呼び、この境界条件を満たす解を求める問題を境界値問題といいます。

例としてこのカテゴリーでは以下のような波動や熱伝導における境界値に関する問題を、フーリエ解析のチャプターにあったフーリエ積分やフーリエ級数を用いてそれらを偏微分方程式によって考察していきます。

◆コンテンツ紹介

波動方程式

双曲線偏微分方程式に関する考察

波動方程式とは、波動の変位に関して時間と座標に関する変数を独立変数としてとらえることのできる定数係数型偏微分方程式（双曲線偏微分方程式）であり、この方程式における境界値に関する問題を、半区間におけるフーリエ積分表示などを使って解いていくことを考えていきます。

この上記方程式におけるを時間と距離の変数を含むものとして次のようにおきます。

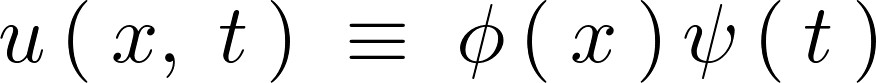
こうすることにより変数分離という形で式をとらえることが可能になります。

これの便利なところは左右それぞれにおいて互いに独立変数とすることができその定数係数を例えばとおいて計算していけることにあります。

次のようにおけることになります。

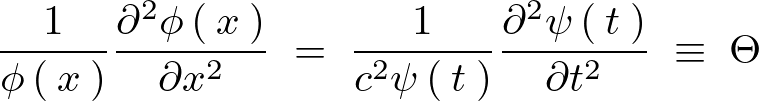
このようにしてそれぞれの微分方程式を条件に分けて計算していくことになります。

熱伝導方程式

放物形偏微分方程式(１次元熱伝導方程式)に関する考察

未知関数を含まない関数を分離できないときを同次といいその同次線形偏微分方程式においては“重ね合わせの原理”というのが成り立ち、がその方程式の解ならば、その線形結合も解となります。

次のような式を考えてみましょう。

変数分離法を使って、をとの関数として二つに分離します。

これを上式に代入すると、

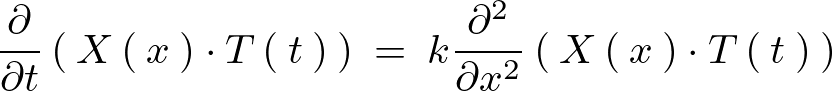
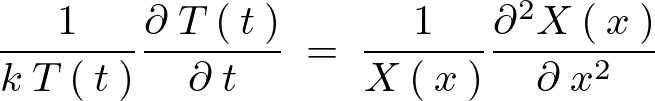
式の両辺をよく見てみるとそれぞれがとだけの関数になっていることがわかります。
上式のようにとを独立に考えても等式が成り立つためには両辺の値が定数であると考えればよいことになります。

この定数をとしてそれぞれの式に対し次のようにおきます。

こうすることによってそれぞれの変数ごとに分かれた次のような微分方程式が導かれます。

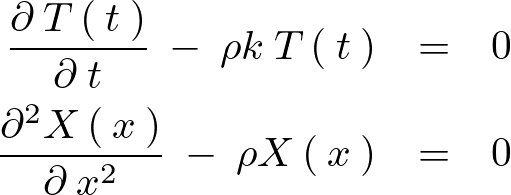
これらの式に対して境界条件を課して解を導いていきます。

無限区間における熱伝導方程式

無限区間における熱伝導方程式（拡散方程式）とフーリエ積分

定区間における一次元熱伝導方程式に対して今度は無限区間における熱伝導方程式を考えます。このとき積分範囲が無限区間になりフーリエ積分表示が適用できるようになります。

熱伝導方程式で使われた上記の微分方程式に対して、同様に次のようにおいて変数分離します。

同様にして次の方程式、

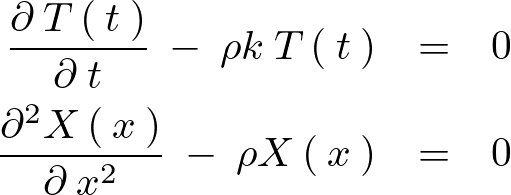
に関して熱伝導方程式と同様に解を導いていきますがこの無限区間における積分においては次のような式の計算が付加されることになります。

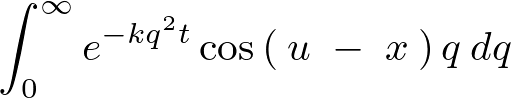
このカテゴリーでは境界値問題に関して以上の内容を取り扱って行く予定です。以下のリンクよりお入りください。