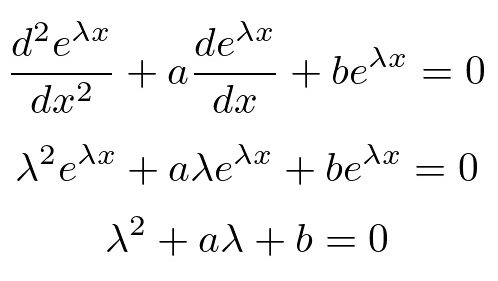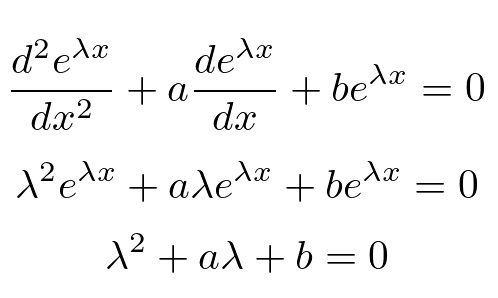ｎ階微分方程式の解

微分方程式に含まれる導関数の階数（ドット数）の一番高いもの（階）を、階の微分方程式といいます。

微分方程式の解には一般解と特殊解というのがあります。基本的にはｎ階微分方程式にはｎ個の任意定数を含むｎ個の一般解があり、さらにはその任意定数Cにおいて初期条件などがついていてその条件のもとでしか求まらない解…いわゆる特殊解とよばれるものがあります。

例題

次に示す微分方程式を求め、そしてその一般解から括弧内の初期条件を満たす特殊解を導いてみましょう。

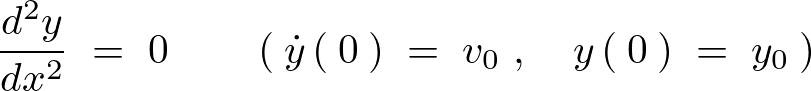
答え

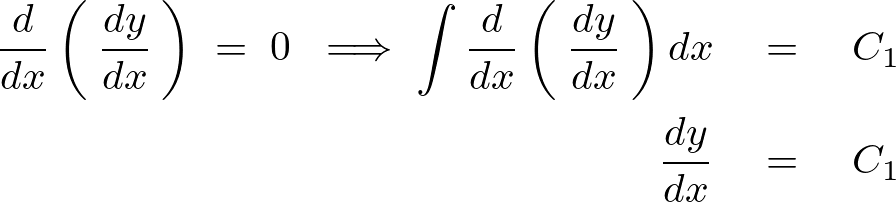
求まった式をさらに両辺に対して積分します。

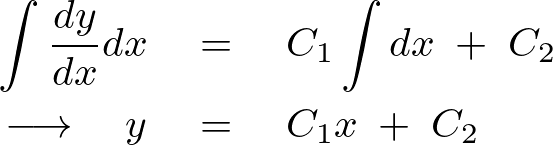
これが求める一般解になります。

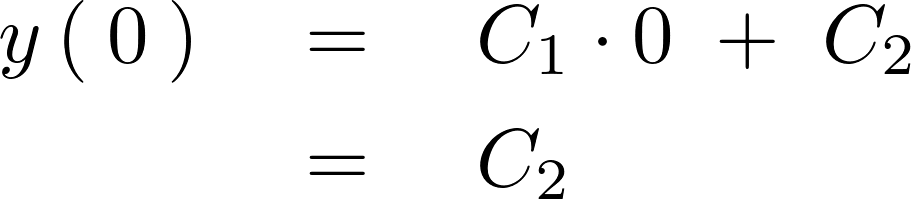
これにより特殊解が次のように求まります。

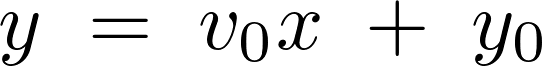
◆コンテンツ紹介

１階常微分方程式

作用素が１階のものを１階微分方程式と呼び、変数が２つある場合それぞれを同じ変数同士で分けて作用素を変化させて計算していきます。

変数分離形

次の形の１階の微分方程式、

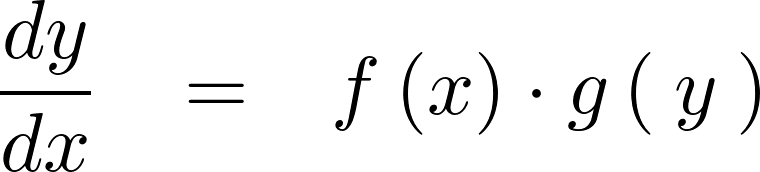
解き方としては、まず変数が２つあるので両辺にそれぞれを“分ける”ということをします。

上記式に関しては、左右の同じ変数を持つもの同士で分けるようにしてそれぞれを移動させると、

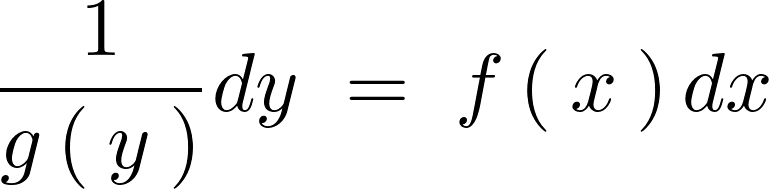
これを両辺にわたって積分します。

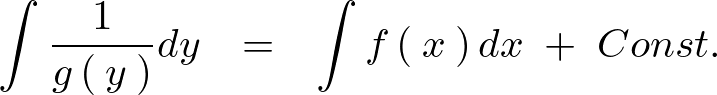
というのは積分整数のことになります。特にことわりがなければ今後と表します。

定型数２階同次微分方程式

オペレータ作用素が２階（２階微分）が入っている以下のような微分方程式を考えます。

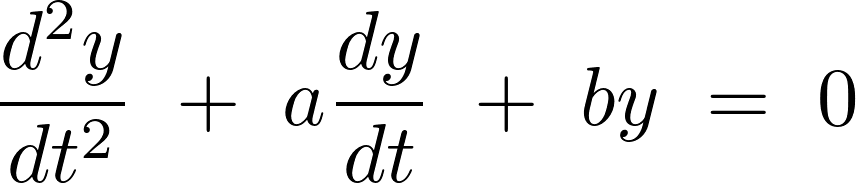
上記微分方程式について考察していく場合、解を次のように、

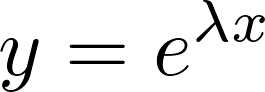
が解であるとします。

これを実際に代入してみると、

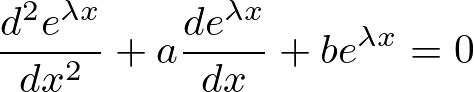
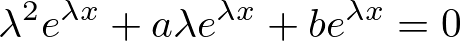
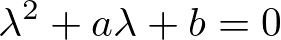
ここで2次方程式とその解の公式は、

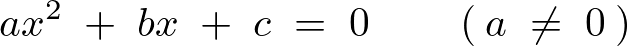
より、

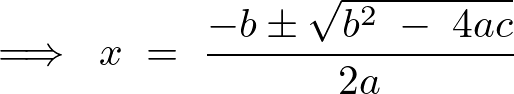
だったのでこれを先ほどの式に当てはめれば、

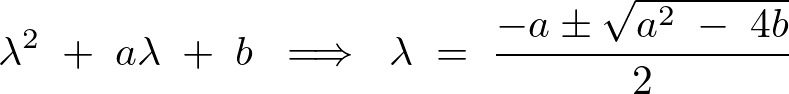
このようにして解を導いていきます。