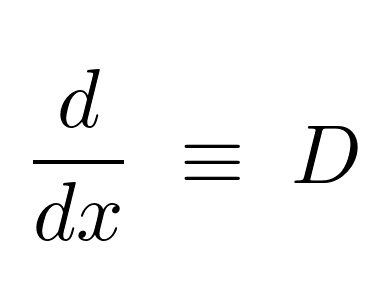微分演算子による連立微分方程式の解法①
微分演算子を使った連立微分方程式の解法
次のような連立微分方程式を考えます。
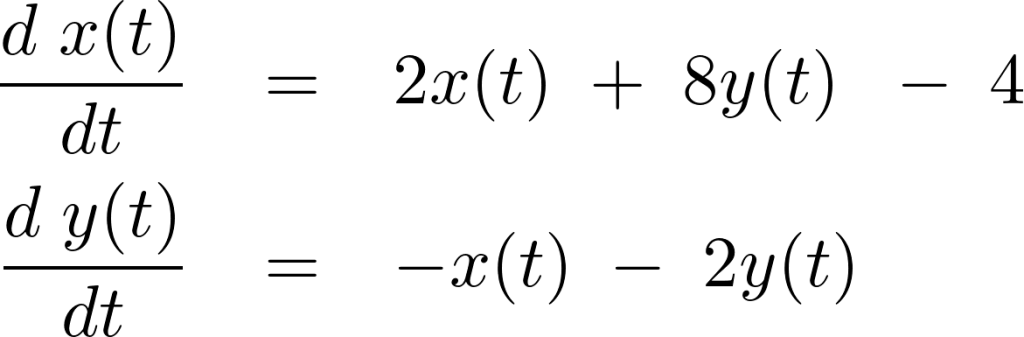
マセマティカで描画するとこんな感じです。
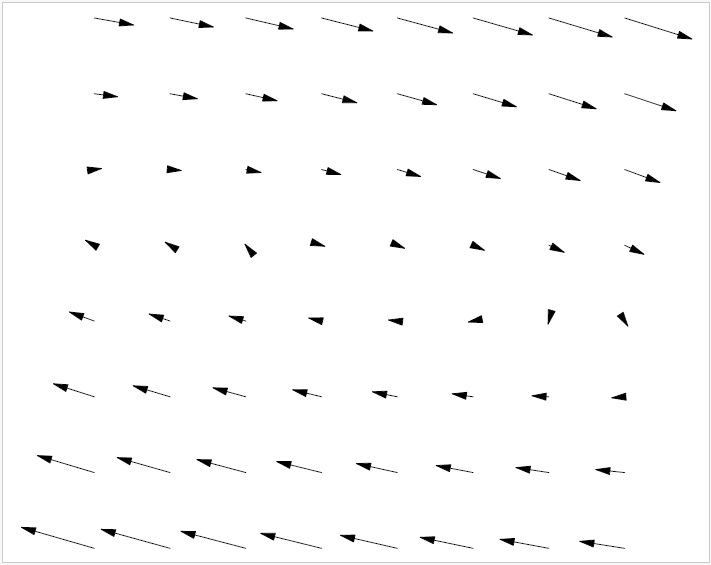
ベクトル描写画像の枠が斜めって見えてますが、それは錯覚になります。
上記の2つの式を次のように置きます。
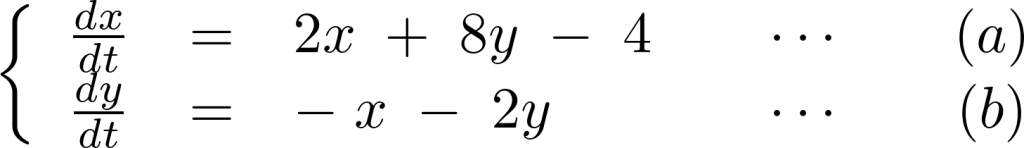
 の式を変形させてそれを
の式を変形させてそれを の式に代入します。
の式に代入します。

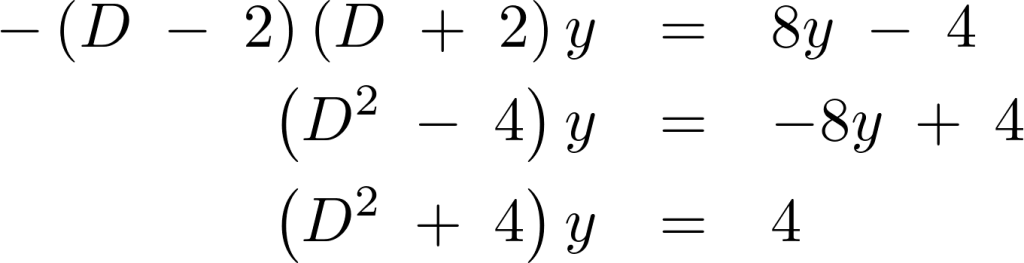
このときの斉次解は、
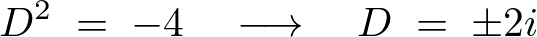
となるのでこれを使って以下、
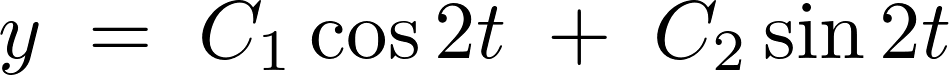
さらに特殊解においては、
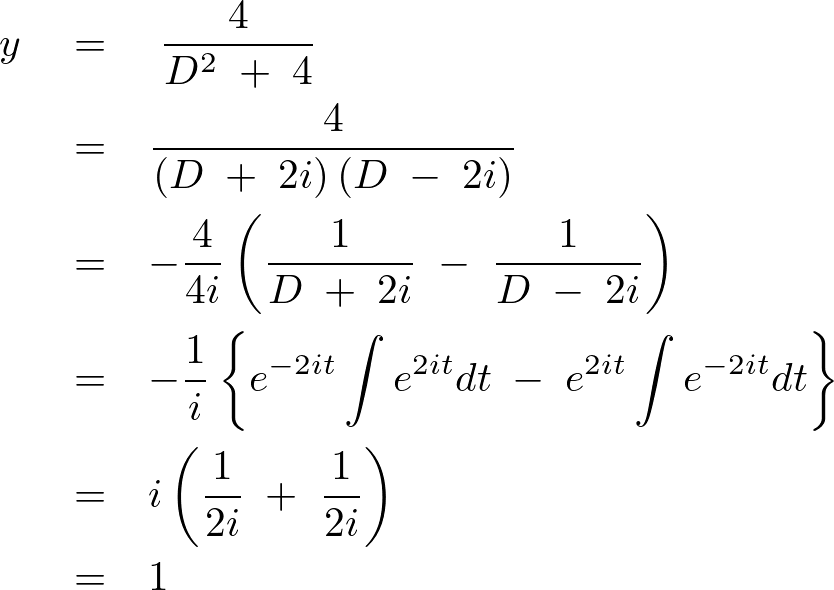
となるので一般解は以下のようになります。
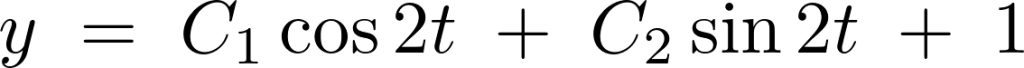
これを一階微分してまとめると以下、
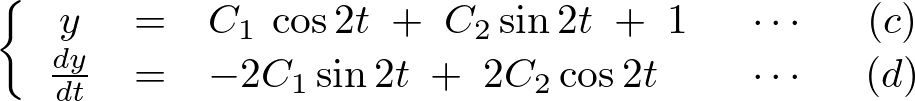
次に上記式の を
を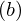 の式に代入して計算していきます。
の式に代入して計算していきます。
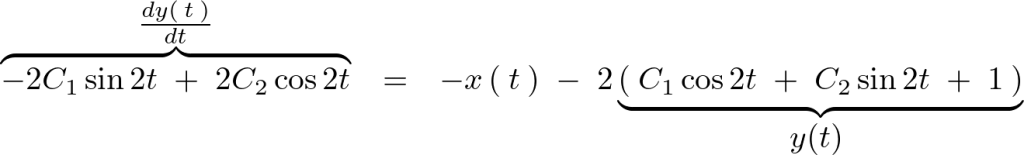
これより、
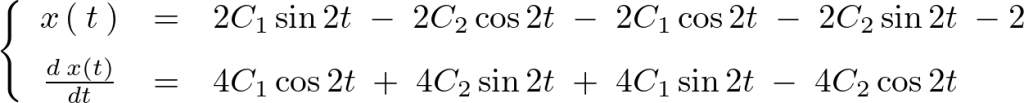
ここでこの一般解に対して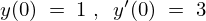 という初期条件を加えると、
という初期条件を加えると、
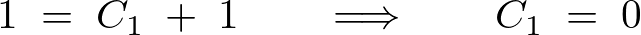
となるので、
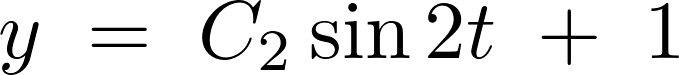
さらに、
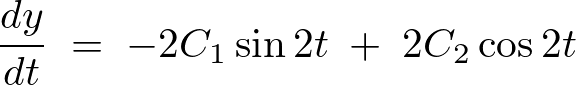
となるので初期条件を加えると、

よって初期条件を加えた場合の一般解は次のようになります。

下の画像は同じ初期条件を満たす場合のこのときの同次解と非同次解との比較をグラフで表してあり、点線が同次になります。
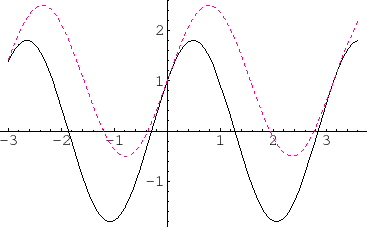

連立微分方程式解法②
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
微分演算子による連立微分方程式の解法①
カテゴリー : 微分演算子による連立微分方程式の解法①オペレータ作用素をD=d/dtのようにおき、それを代数的に取り扱うことによって連立微分方程式の解をシステマティ…