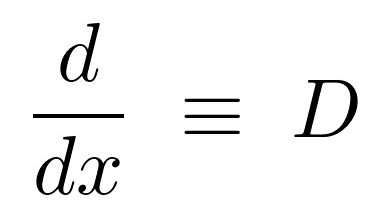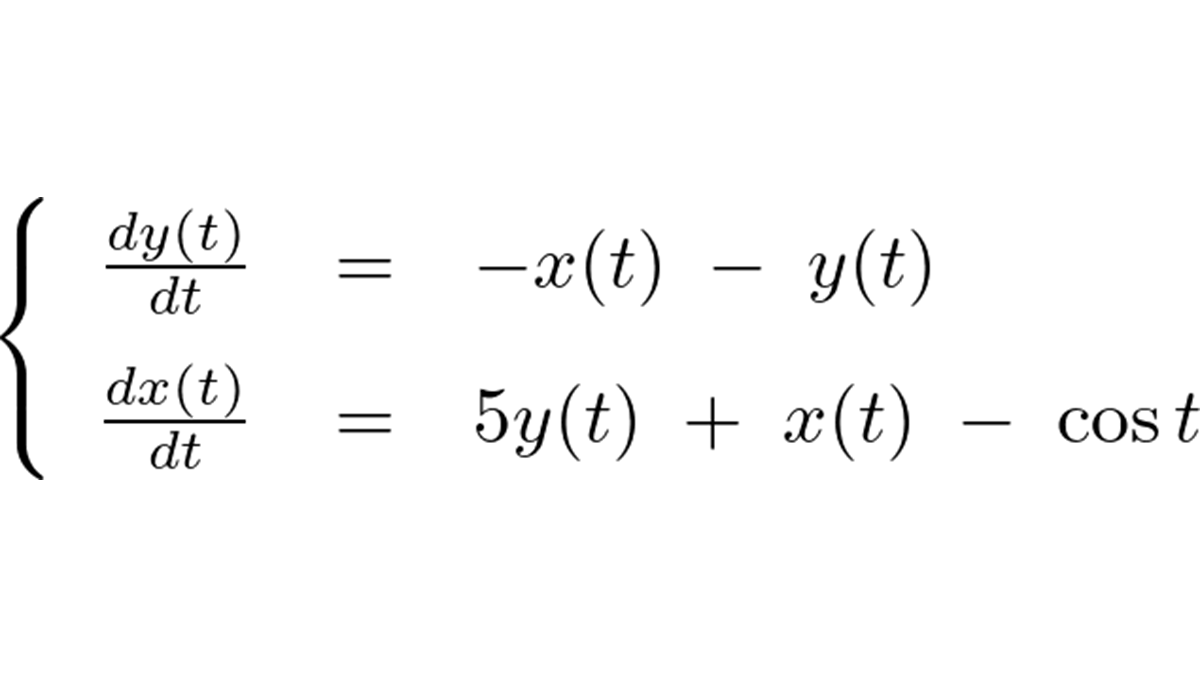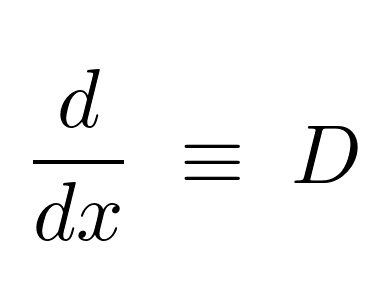ヘヴィサイド演算子とは

微分演算子の表記

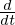ある関数を、例えばで微分する場合は左側からのように演算子を“作用”させ、そしてそれらに働きかけて関数そのものを変化させます。

こういったものを作用素といい、この場合は時間ですが、それ以外にもや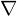（ナブラ）、さらにはダランベルジャンなどもその作用素（オペレーター）と呼ぶことができます。

演算子法とはその作用素自体を記号のなどとし、そしてそれを通常の“代数”（例えば分数）のように扱うちょっと変わった計算法になります。

いまの関数をとした場合、この時のヘヴィサイド微分演算子の表記の仕方は以下のようになります。

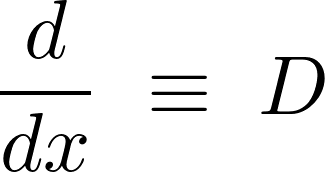
なので例えば、に対して上記の演算子を作用させれば、

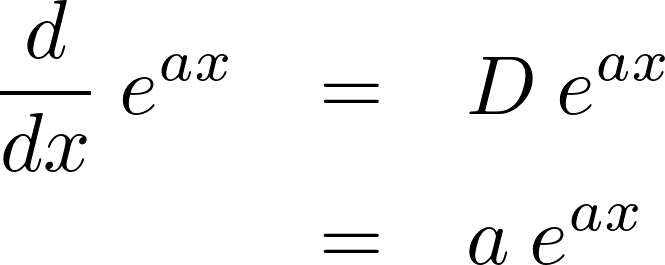
通常は例えばの関数をとした場合、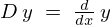といった表現を意味し、微分方程式における以下のような表記、

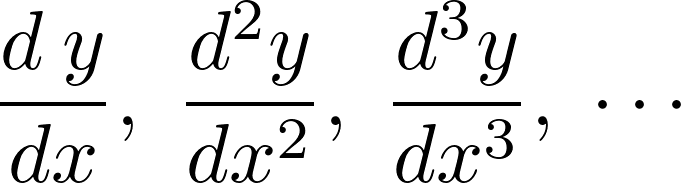
は以下のような表現をすることになります。

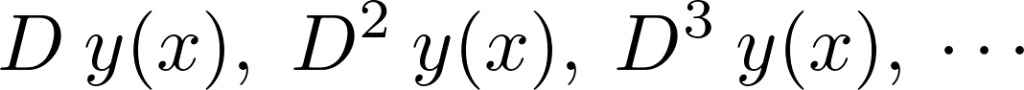
逆演算子

通常は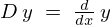であるので、これの逆数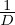は積分を意味していると考えるようにします。

例えば、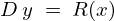であるとするならば、

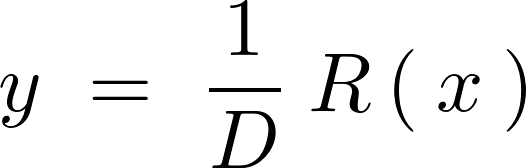
であり、

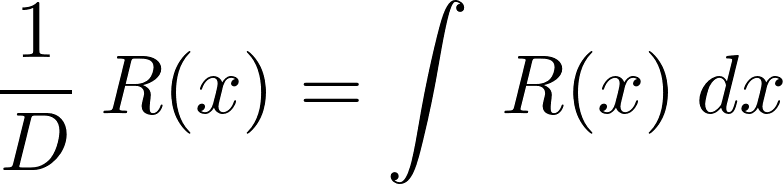
といったことを意味しています。

今ここで次のような関数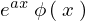を考え、それに対して微分演算子を作用させます。

積の微分により、

またさらに次のような関数、

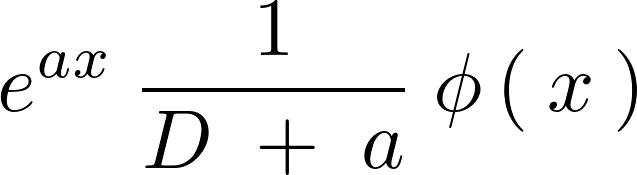
に対しても上記の場合と同じようにを作用させて計算すると、

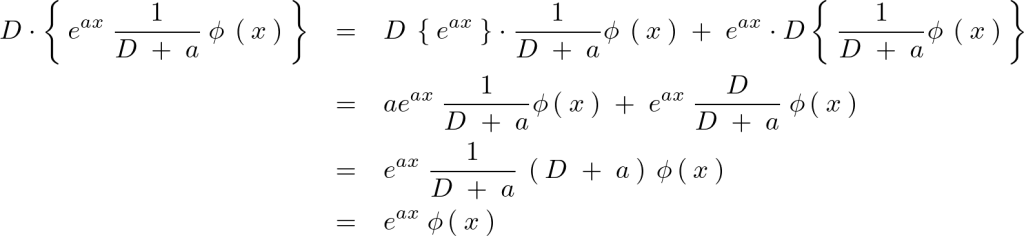
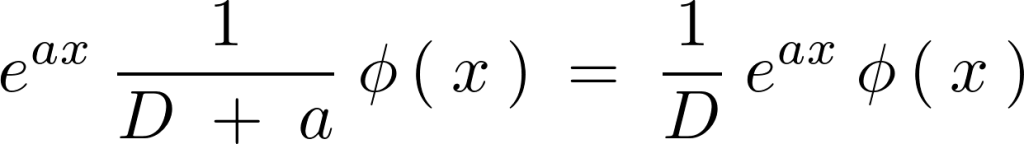
この計算結果を逆にとらえれば、

となり、微分演算子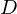の逆数を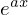に作用させると右辺のように変化するのだと考えることができます。

このカテゴリでは微分演算子を使った微分方程式、特に連立微分方程式の解法について詳しく解説しています。以下のコンテンツよりお入りください。