フーリエ級数
フーリエ級数とは
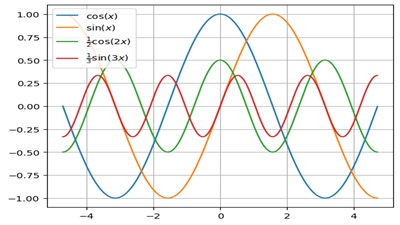
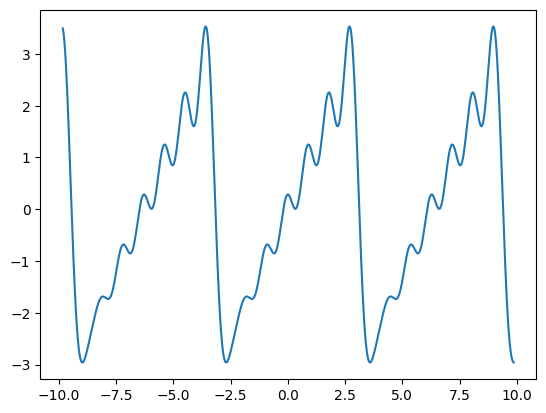
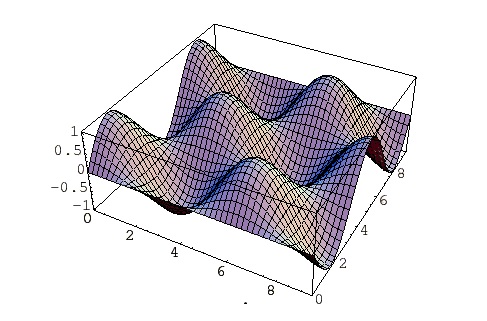
フーリエ級数とは、ある複雑な周期関数に対して、サインやコサインなどの三角関数を使ったより簡単な形で表現できる周期関数の無限級数和によって展開された一連の関数のことをさします。一般的にフーリエ解析といえばこのフーリエ級数が起点となっています。
◆コンテンツ紹介
フーリエ級数展開
フーリエ級数展開は、ある複雑な周期的関数に関して次のように和の形に展開できることを意味します。
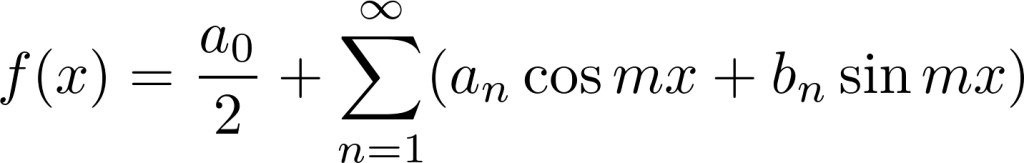
式中の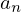 および
および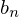 に関しては以下のようなものになります。
に関しては以下のようなものになります。
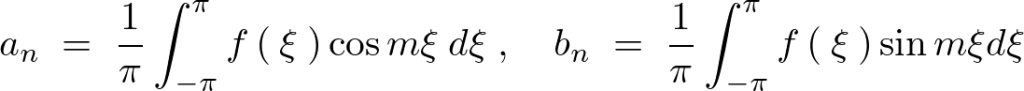
式を見てわかるように区間内において展開されている関数が和の形にきれいにまとめられています。
このコンテンツではこの式における係数の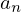 および
および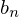 を三角関数を使って求めこの公式を実際に導き出し、かつある周期的な関数における実際のフーリエ級数展開までを行っていきます。
を三角関数を使って求めこの公式を実際に導き出し、かつある周期的な関数における実際のフーリエ級数展開までを行っていきます。
フーリエ余弦展開・正弦展開
一般的に![]() または
または![]() とする関数においてその周期がグラフに対して左右対称かまたは非対称に分かれています。
とする関数においてその周期がグラフに対して左右対称かまたは非対称に分かれています。
こうした場合、その遇奇性により![]() は
は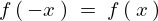 なので遇関数、
なので遇関数、![]() は
は のため奇関数であるといえます。
のため奇関数であるといえます。
このことは求めるフーリエ級数展開において![]() が遇関数、または奇関数のどちらか一方であったならばそのフーリエ係数
が遇関数、または奇関数のどちらか一方であったならばそのフーリエ係数![]() または
または![]() のどちらかが
のどちらかが![]() になると考えることができます。
になると考えることができます。
偶関数による余弦展開
例えば関数![]() が遇関数
が遇関数![]() でるとした場合、
でるとした場合、![]() に拡張し、周期
に拡張し、周期![]() の周期関数にすると、この周期関数のフーリエ級数展開は次のようになります。
の周期関数にすると、この周期関数のフーリエ級数展開は次のようになります。


奇関数による正弦展開
さらに今度は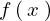 が
が であるという奇関数であれば
であるという奇関数であれば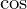 項の
項の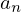 が
が になってしまうので周期
になってしまうので周期 ののフーリエ級数展開式はフーリエ級数展開は
ののフーリエ級数展開式はフーリエ級数展開は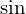 項だけが残ります。
項だけが残ります。
これにより、


となります。
これをフーリエ正弦展開といいます。
このコンテンツではこういった性質を利用してある周期的な関数を偶関数奇関数に分けて展開していくことを考えていきます。
このカテゴリーではある区間において周期的に展開される関数のフーリエ級数についていろいろな視点から考察していきます。

準備中
準備中

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.