フーリエ余弦・正弦展開
フーリエ余弦・正弦展開とは
フーリエ級数展開における遇関数と奇関数の違い
![]() と
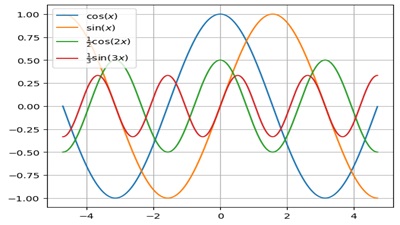
と![]() のグラフを見て分かるように
のグラフを見て分かるように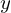
![]() 軸を中心軸として考えるとそれぞれが左右対象と非対称に分かれています。
軸を中心軸として考えるとそれぞれが左右対象と非対称に分かれています。
このため、その偶奇性により![]() は
は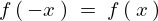 なので偶関数、
なので偶関数、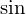 は
は なので奇関数であるといえます。
なので奇関数であるといえます。
求めようとしているフーリエ級数展開において が偶関数、または奇関数のどちらか一方であったならばそのフーリエ級数
が偶関数、または奇関数のどちらか一方であったならばそのフーリエ級数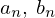 の
の![]() 、もしくは
、もしくは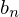 のどちらかいっぽうが
のどちらかいっぽうが![]() になります。
になります。
偶関数による展開
例えば、関数![]() が偶関数
が偶関数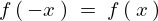 であるとし
であるとし![]() に拡張して周期
に拡張して周期![]()
 の周期関数にすると、この周期関数のフーリエ級数展開式は
の周期関数にすると、この周期関数のフーリエ級数展開式は![]() 項をのぞいた次のような式になります。
項をのぞいた次のような式になります。


奇関数による展開
また![]() が奇関数であるならば今度は
が奇関数であるならば今度は![]() が
が![]() となってしまうので周期
となってしまうので周期![]() のフーリエ級数展開は
のフーリエ級数展開は![]() 項だけが残ります。
項だけが残ります。
これにより今度は次のようなフーリエ級数展開式になります。


これをフーリエ正弦展開と呼びます。
正弦・余弦級数の分離
このように考えれば関数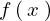 は偶関数を
は偶関数を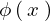 、奇関数を
、奇関数を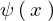 としてこれを以下のようにおきます。
としてこれを以下のようにおきます。
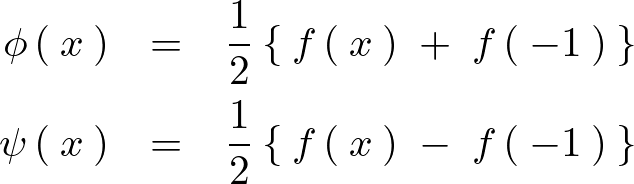
こうすることによって以下のような和のかたちとして次のように書くことができます。

実際に上記に述べたやり方で次の関数をフーリエ展開してみましょう。
遇関数の余弦展開
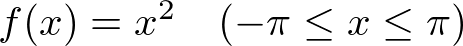
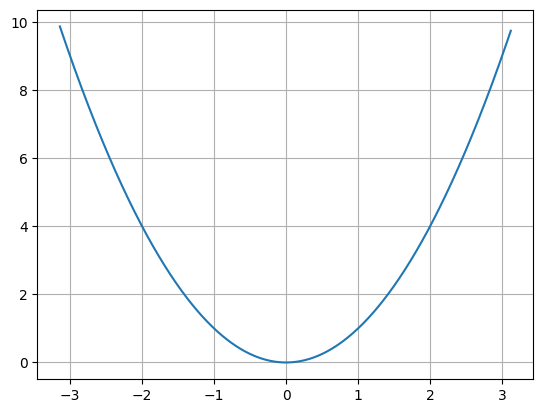
図は上記偶関数をpythonによってグラフ化したものになります。
グラフからみてわかるように![]() は偶関数なので
は偶関数なので![]() となります。
となります。
 の導出
の導出
まず![]() から計算していきます。公式より、
から計算していきます。公式より、
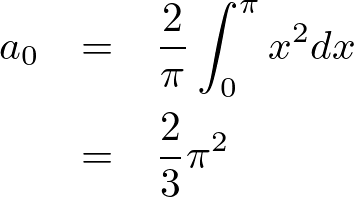
 の導出
の導出
次に![]() を計算していきます。
を計算していきます。
ここで、

といった部分積分を使って計算していきます。


求まった![]() 、
、![]() を余弦展開の式に代入します。
を余弦展開の式に代入します。
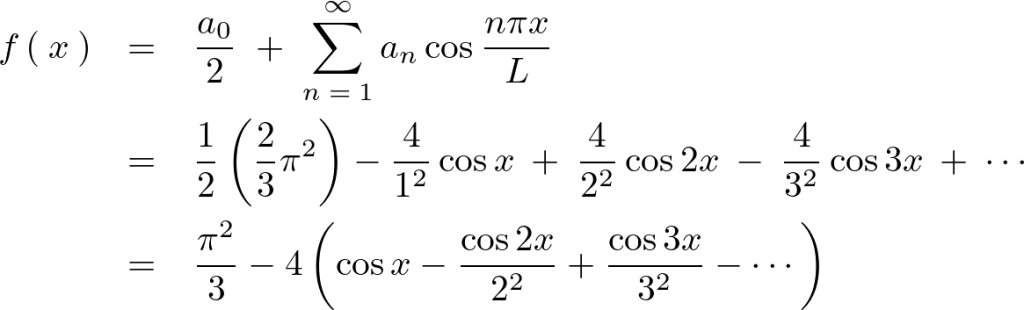
和の式でまとめれば以下のようになります。

ここで周期を![]() とすると、
とすると、

展開していけば次のような級数展開式が求まります。
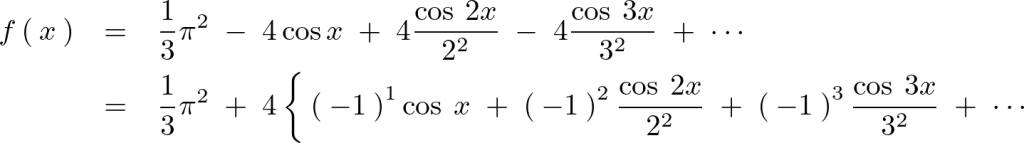

奇関数の正弦展開


図をみてわかるように左右非対称になっているのでフーリエ正弦展開が適用できることになります。
なので今度は![]() 、
、![]() となります。
となります。
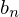 項の導出
項の導出
先ほどと同じように部分積分を適用して計算していきます。

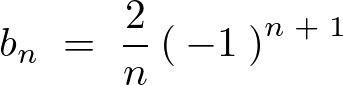
この求まった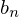 をフーリエ正弦展開の式に代入します。
をフーリエ正弦展開の式に代入します。

先ほどと同じように周期を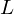 としてまとめれば以下のようになります。
としてまとめれば以下のようになります。
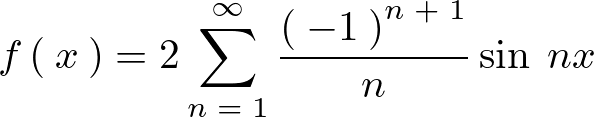
展開していけば次のような式が得られます。


Wait a moment
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Wait a moment
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.