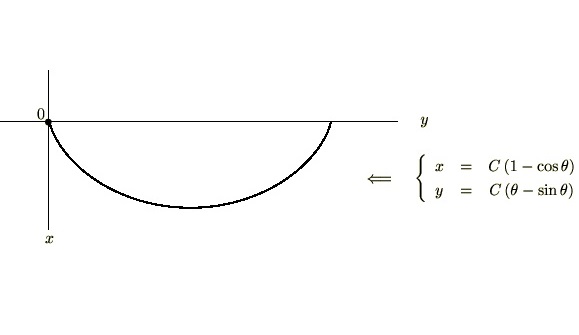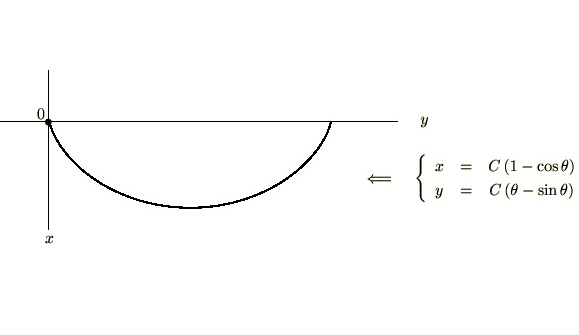最速降下曲線問題とは、ある質点が曲線に沿って点から点まで移動したとき一番短い時間で到達するような曲線はどんなものかと考える問題です。カテゴリ名に“～問題”と付け足していることにたいして意味はないのですが、理由的にはヨハンベルヌーイというひとに関係しています。

座標を軸に平行に、軸を鉛直下向きにとるとある質点の速さに関しては、

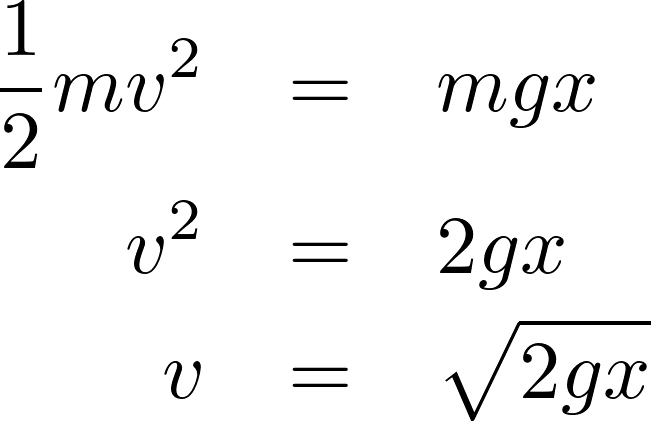
微小線要素については、

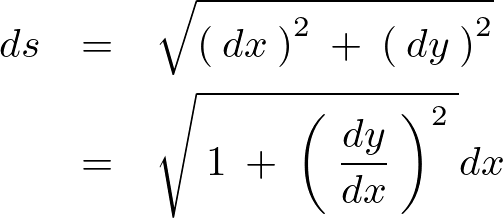
と考えることが出来るので、は、

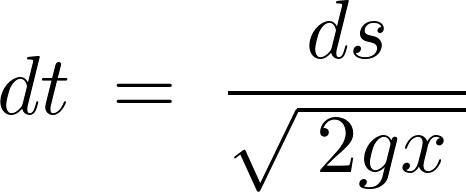
ここで時間の積分を作ります。

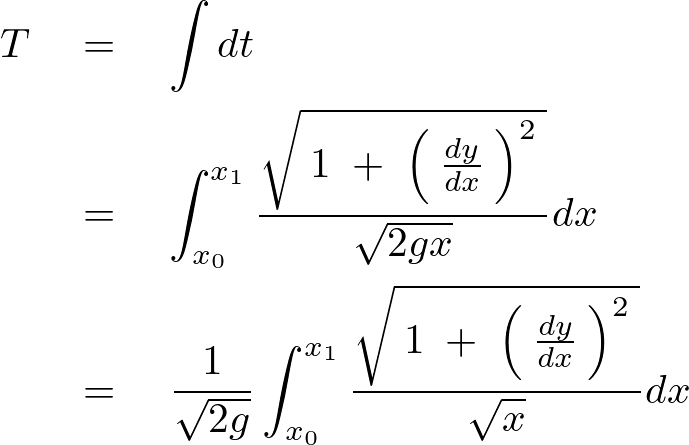
この出てきた積分が最小値になるものを求めていきます。

まず最初に、

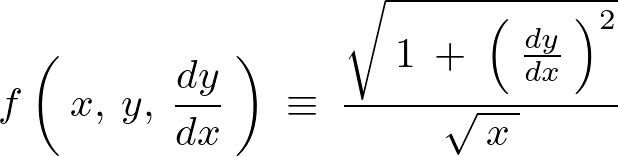
として、であると考えた場合の次のオイラー・ラグランジュの方程式を計算します。

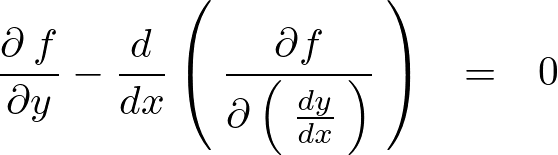
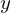の偏微分（左辺第１項）に関してのオイラー式

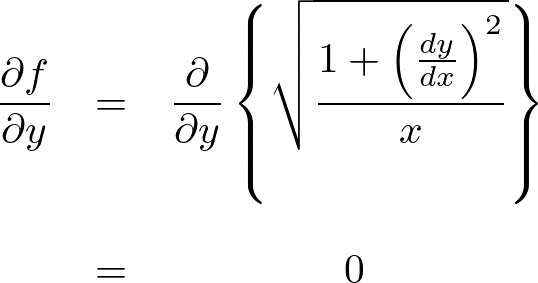
の偏微分（左辺第２項）に関してのオイラー式

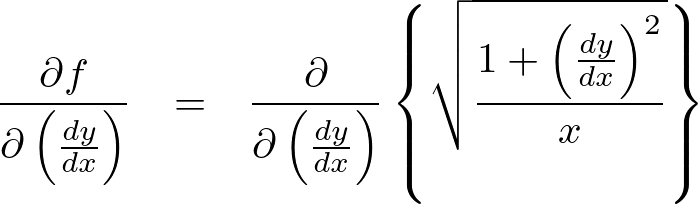
上記式をで微分していくには次のような過程を用いています。

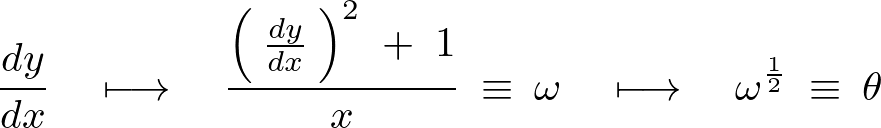
とに関して以下のようにしてそれぞれ微分していきます。

求まったそれぞれをチェインして計算していきます。

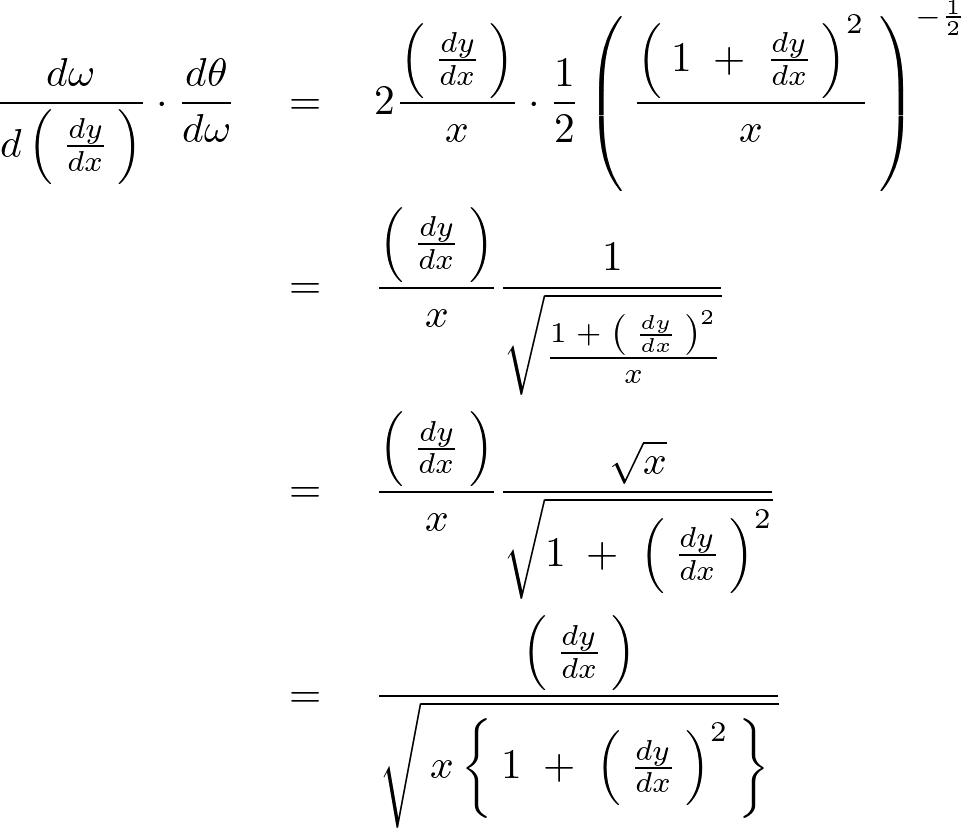
となるのでの部分に関してのオイラーの式は以下のようになります。

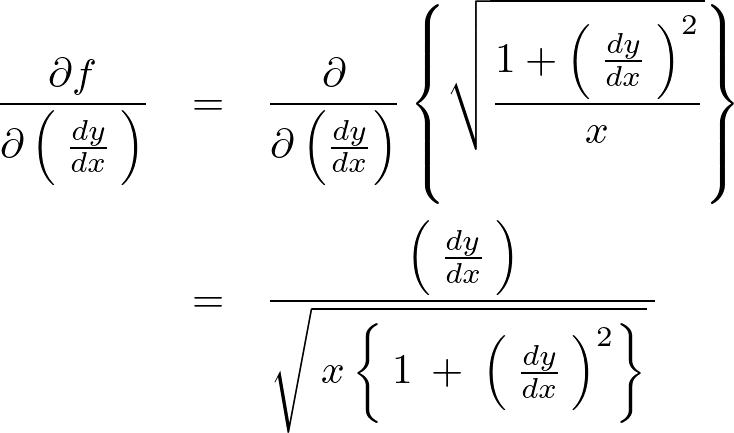
こうしてそれぞれ求まったので先ほどのオイラー・ラグランジュ方程式をもってきて次のように代入します。

両辺をで積分します。

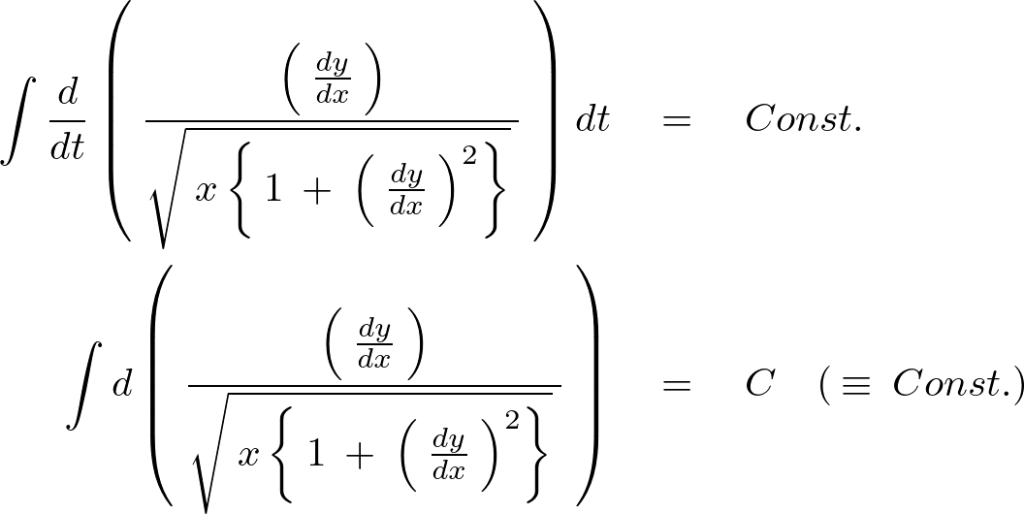
となるので以下のようになります。

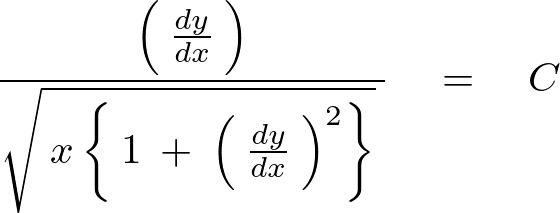
この式で出てきた積分定数を次のようにと置きましょう（あくまで数学的なテクニックです）。

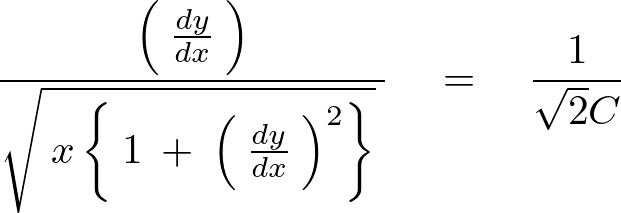
これを変形していきます。

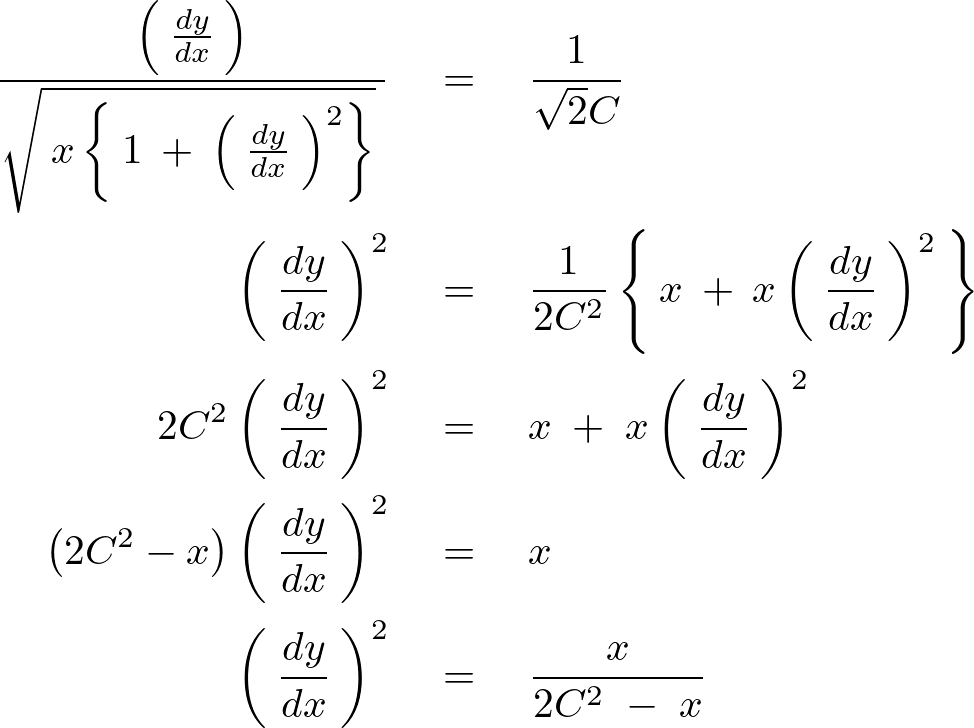
以下のように求まります。

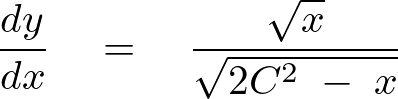
さらに今度はとおく変数変換をします。

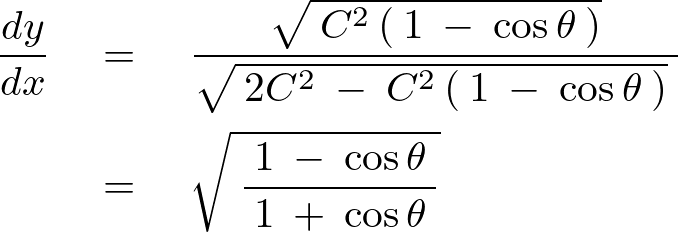
ここで次のような三角関数の性質を使います。

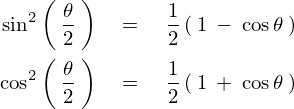
そうすると次のようになります。

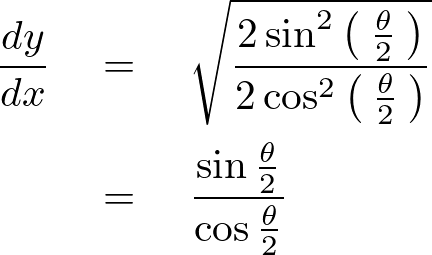
こうすることによって次のように求まります。

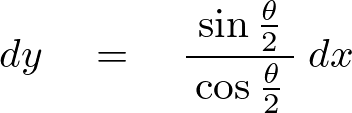
ここで先ほどのを次のように微分します。

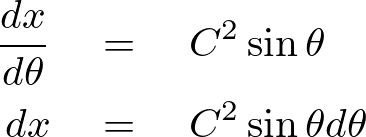
これを代入します。

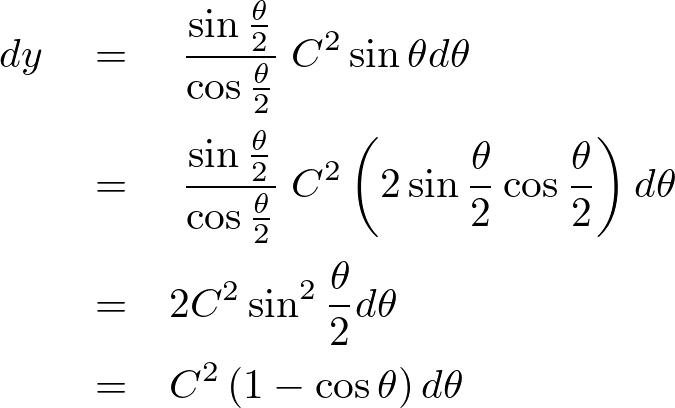
この式の両辺を積分すれば、

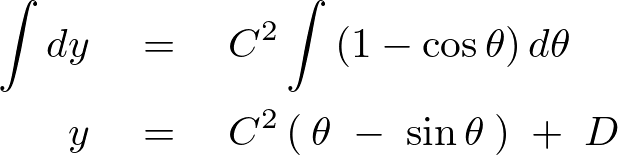
ここで初期条件を考えると時間がのときはでなので出てきた積分定数は。

さらには定数なので簡単にと置きましょう。
したがって求める最小降下線の式は次のようになります。

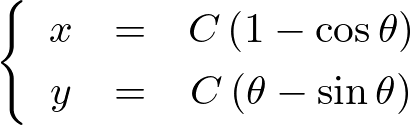
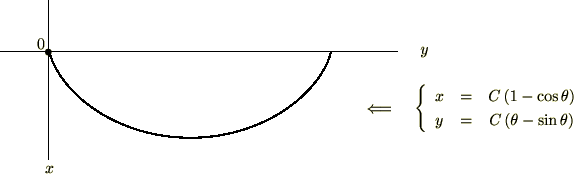
上記曲線図形は一般的にサイクロイドと呼ばれているものになります。

15世紀後半にヨハンベルヌーイというひとがその当時の数学者全体への問題として提起したものとしても有名なものになります。