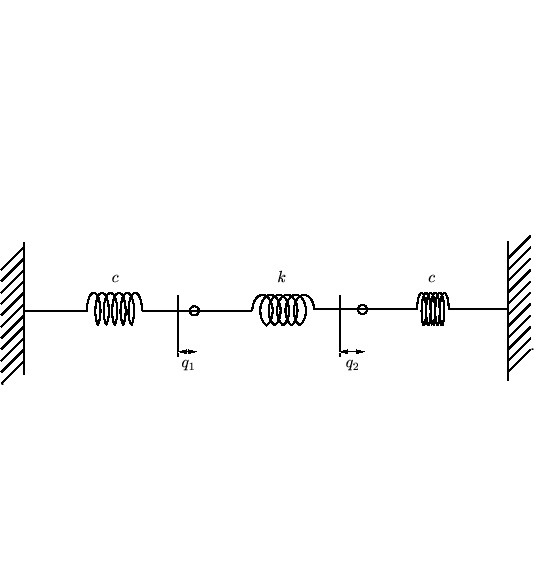
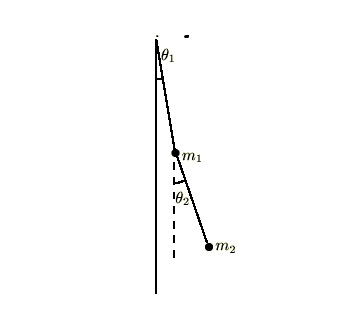
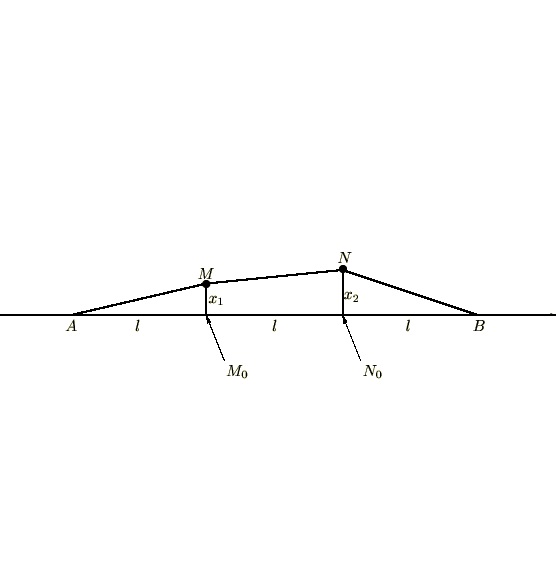
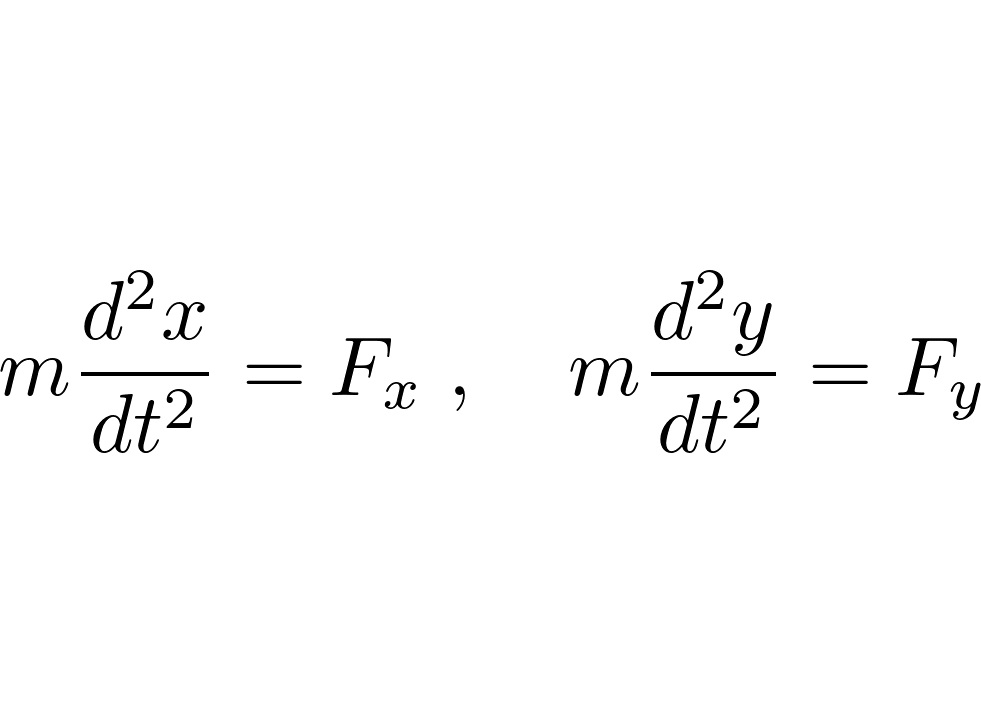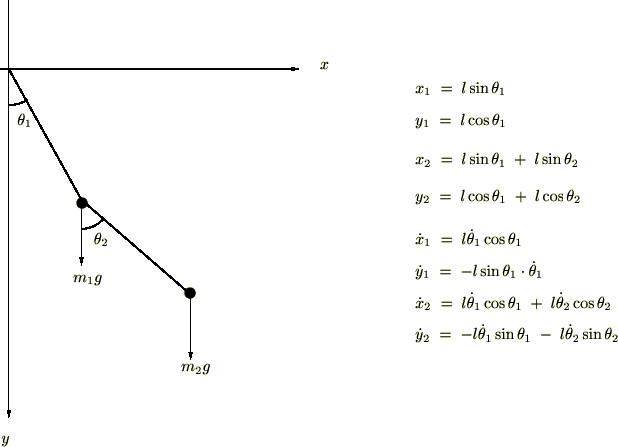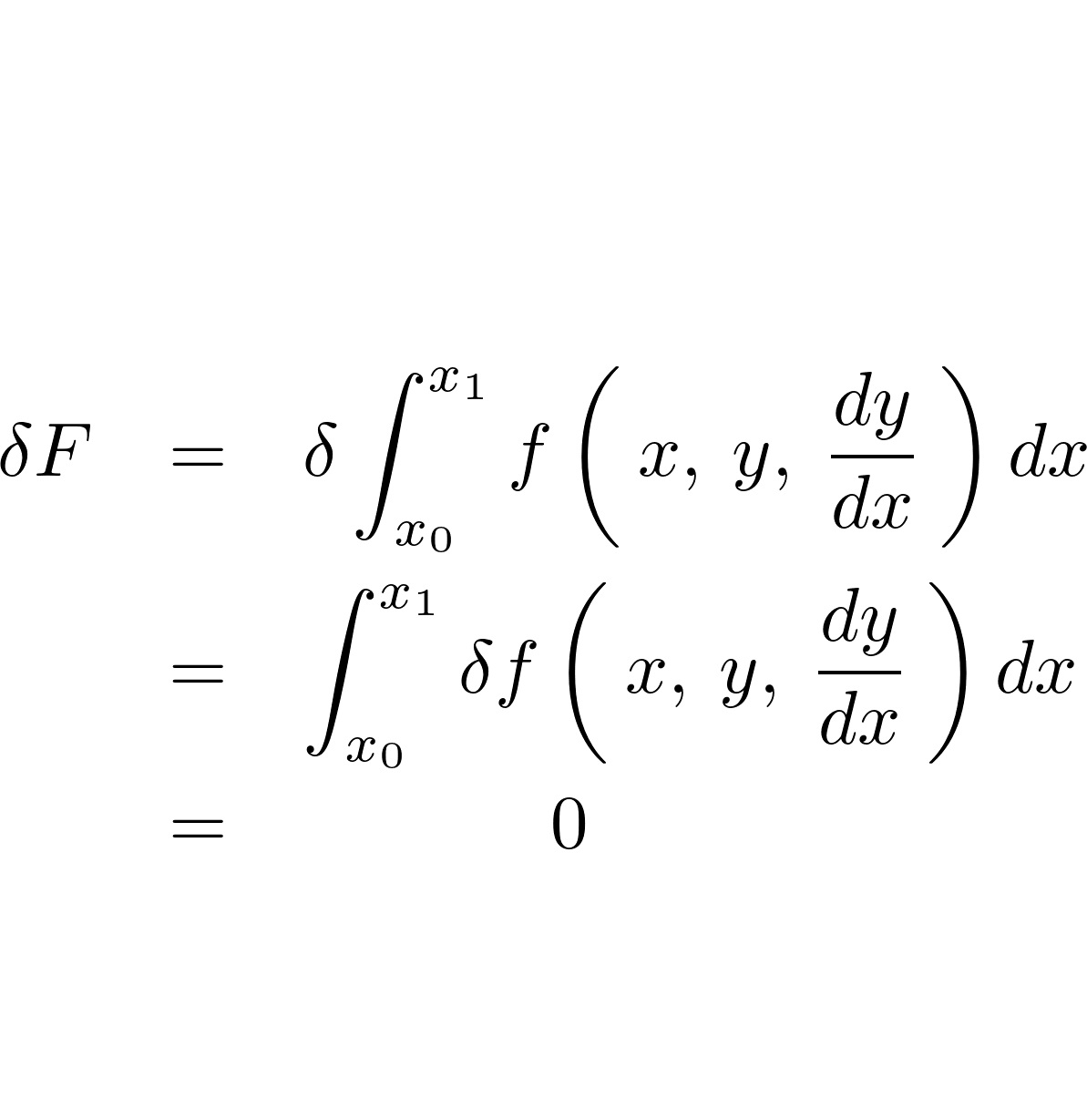解析力学とは

━ エレガントな古典物理学への招待

○解析力学とは、簡単に説明すればニュートン力学における運動方程式の記述を座標変換などの解析的な手法を用い、力学の現象を数学的に洗練された形にあらためて表現しなおしたものをいいます。

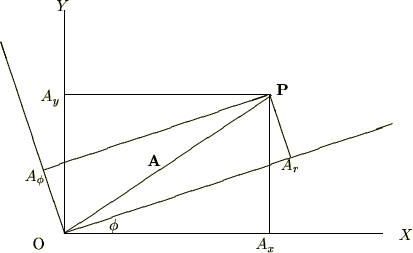
座標変換の簡単な例━【ベクトルの回転変換】

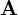原点を共通にの周りに反時計回りに角度だけ回転させた直交座標系を極座標座標系とし、元の座標系座標系との関係をベクトルを使って以下の用の表現します。

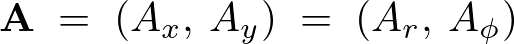
座標変換

、座標を極座標変数で表すと、

これを時間で微分します。

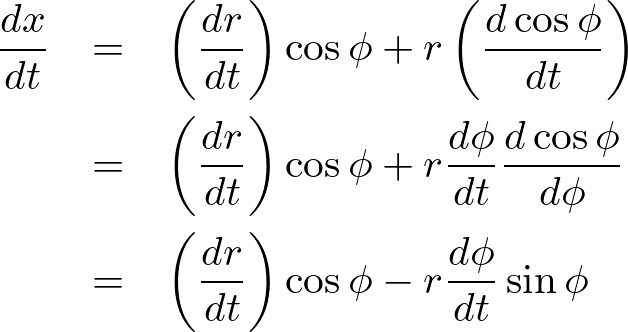
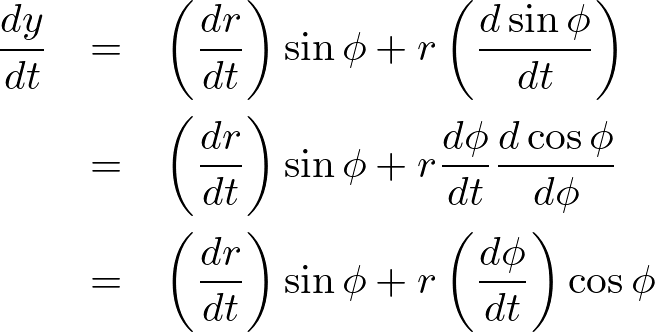
ここで、

とすれば、

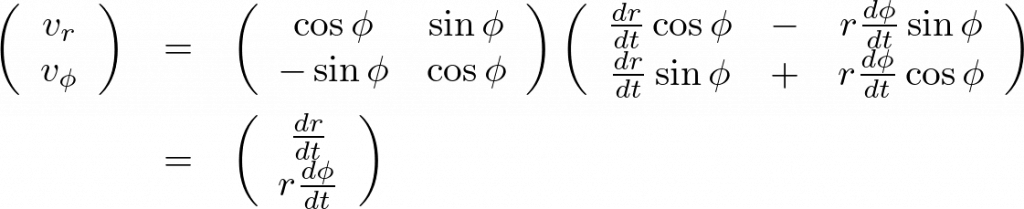
さらに直交座標系における加速度成分を示すと、

これらにより極座標系による加速度成分を求めれば、

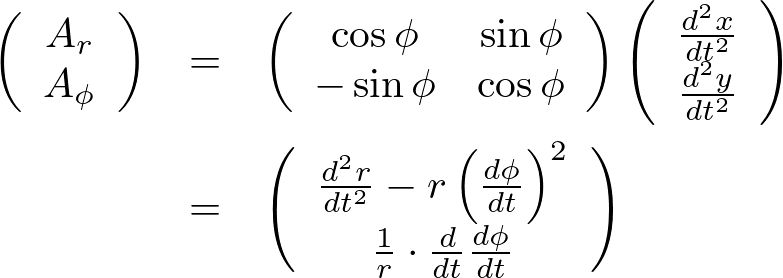
以下のように計算していきます。

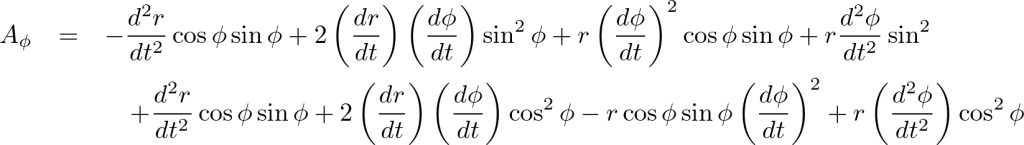
タイトルにでかでかと“解析力学”と書いてますが、内容的にはラグランジュ方程式、オイラー方程式の組み立て方、オイラー式を使った問題などの基本的な部分と、変分原理に関して典型的な事項についてのみ軽く説明してるだけなのであまり詳しくはやっていません。

あくまで初学者、あるいは一般の方が、解析力学というものはどんなものかと知るような場合に適した内容になっているかと思います。ただしある程度の微分積分学の知識が必要です。