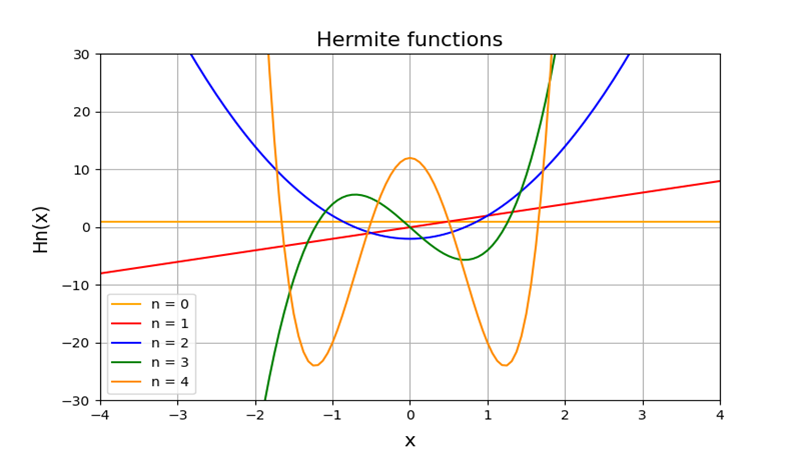
エルミート多項式の諸性質①
エルミート多項式の変形
今ここでロドリーグの式を思い出すと次のようなものになります。
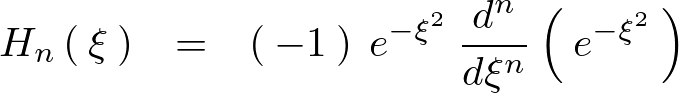
上記式に関して一回微分します。
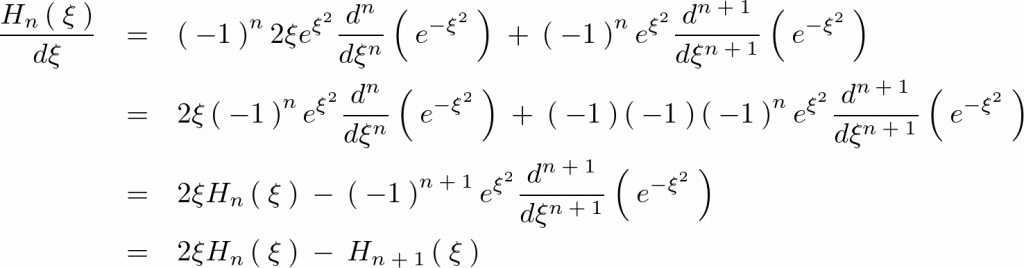

さらに続けて微分します。

上記式においての右辺第4項目を計算していきます。
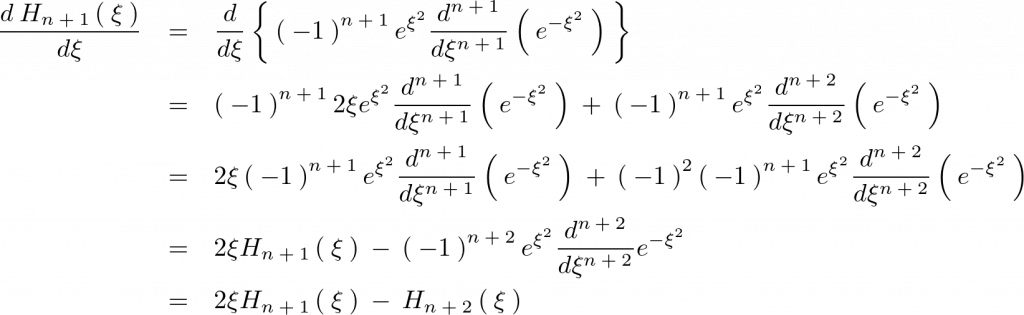
となるので次のような関係式が導かれます。
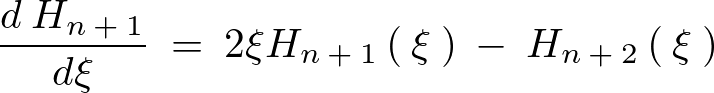
この式を先ほどの の式に代入して計算していきます。
の式に代入して計算していきます。
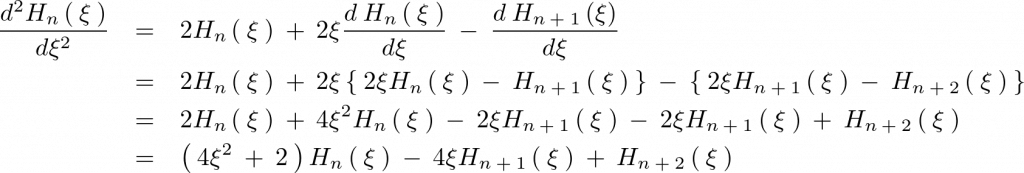
となるので以下の3つの関係式が求まります。
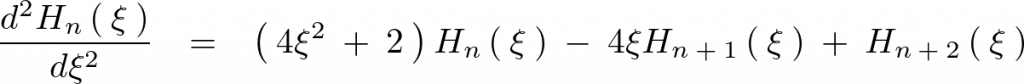

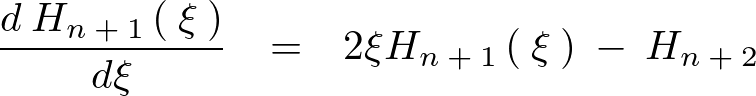
今ここでエルミートの微分方程式を思いだすと、

これに代入します。
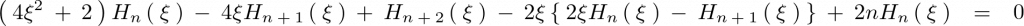
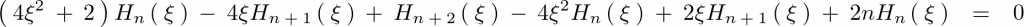

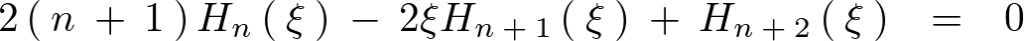


ここで上記式において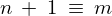 と置きます。
と置きます。
そうして先ほどの式に関して次のようにいったんおきます。

この![]() を
を![]() とおいて、先ほどの次のような式、
とおいて、先ほどの次のような式、

この式の右辺第1項に代入します。
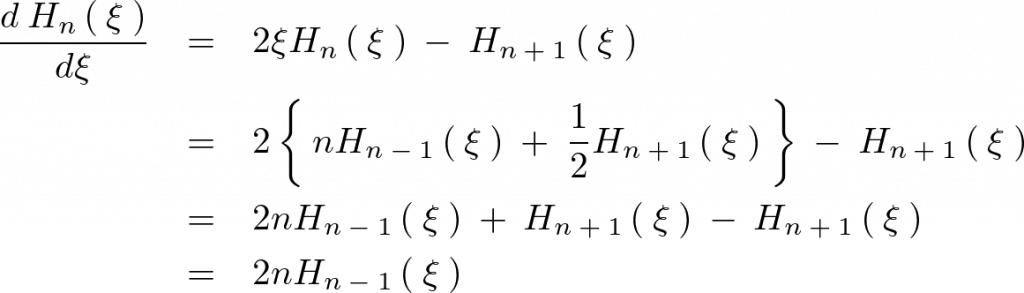
結果的に次のような関係式が求まります。
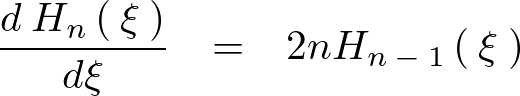
-
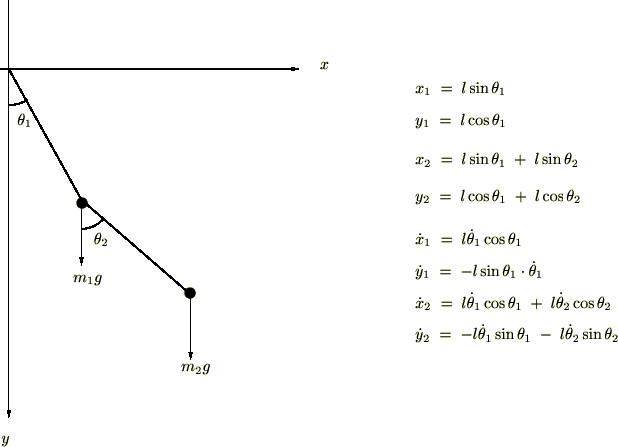
2重振り子②-微小でない場合
続きを読む
-
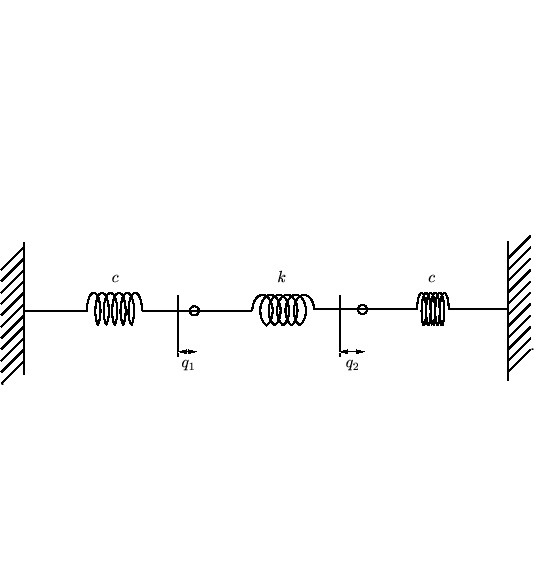
連成振動の解②━3重ばねの振動
続きを読む
-
2重振り子①-微小な場合
続きを読む
-
連成振動の解①━弦の振動
続きを読む
-

ヘヴィサイド演算子法
続きを読む
-
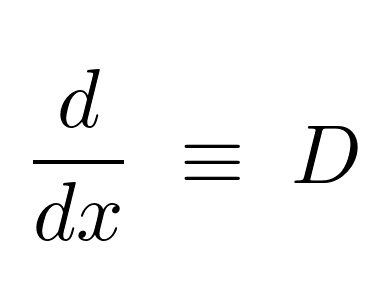
微分演算子による連立微分方程式の解法①
続きを読む