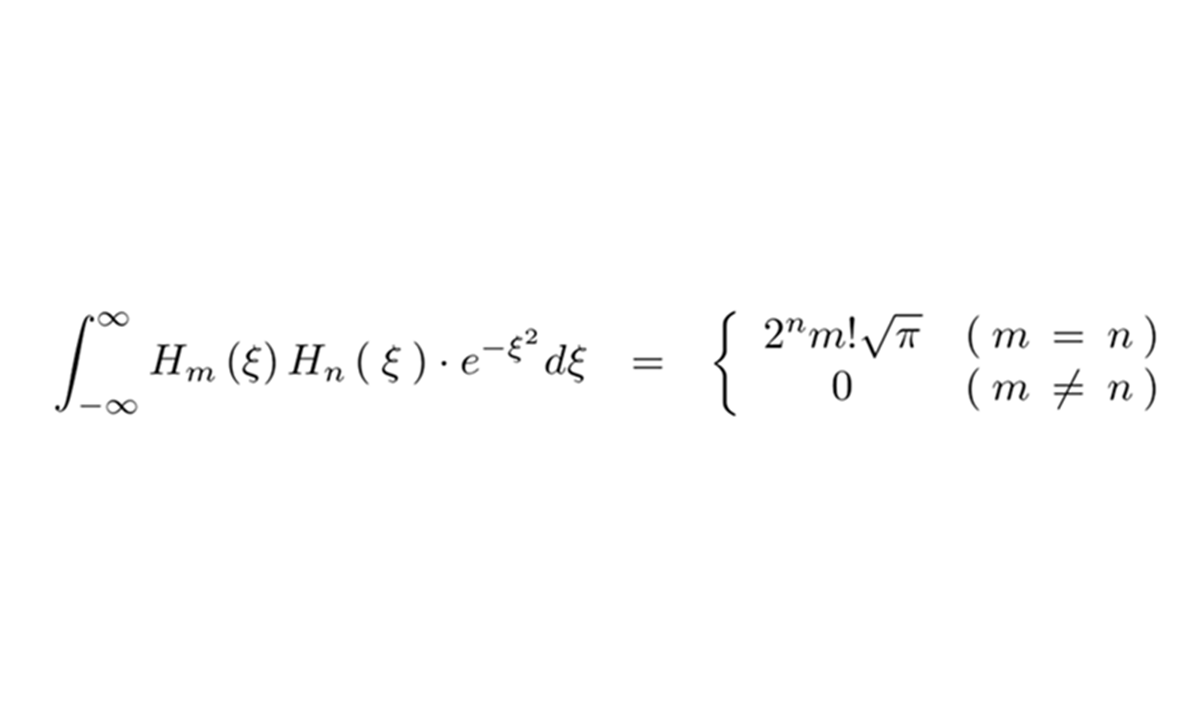エルミート多項式の直交性
エルミート多項式の定義式
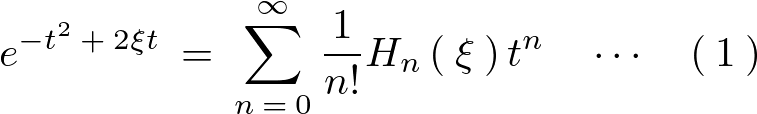
ここでもう一つの定義式の変数を![]() として次のように置きます。
として次のように置きます。
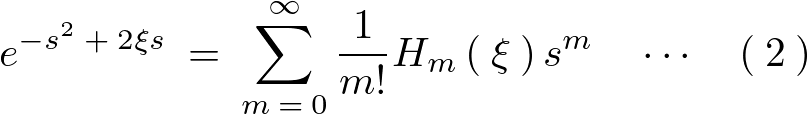
上記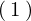 式の両辺に対して、
式の両辺に対して、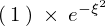 します。
します。
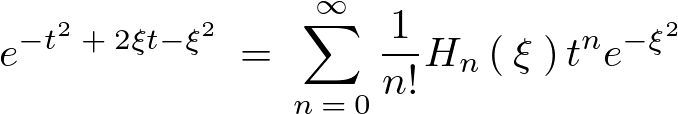
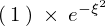 した式と
した式と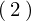 を辺々かけ合わせます。
を辺々かけ合わせます。
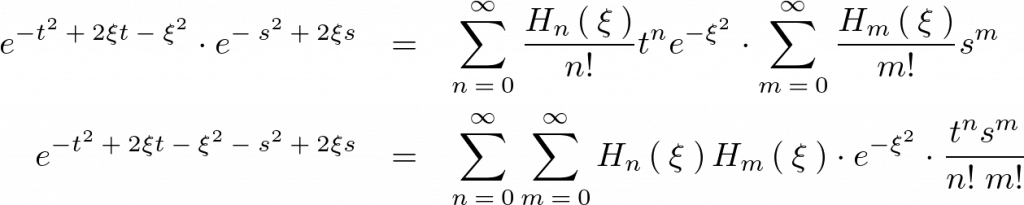
ここで上記式の左辺乗数部分を次のようにして式変形をしていきます。
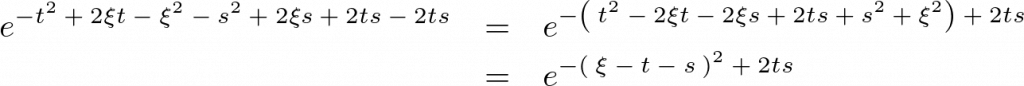
以下のような関係式が導かれます。
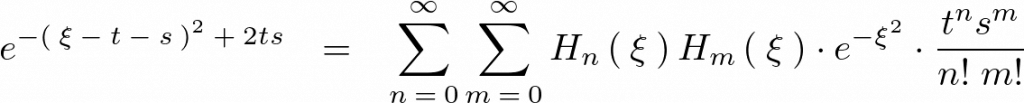
この導かれた上記関係式に対して![]() で
で![]() から
から![]() まで積分します。
まで積分します。
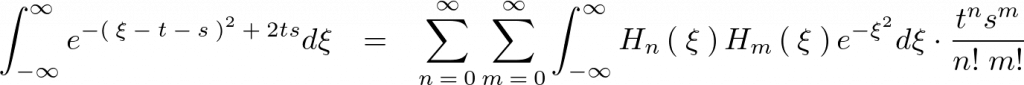
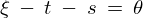 と置くと、
と置くと、
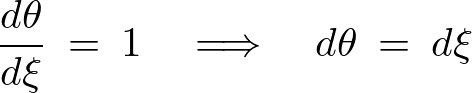
左辺に関して、
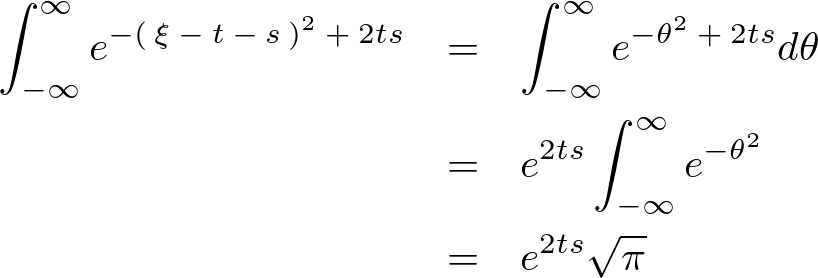
よって、以下のような式が導かれます。
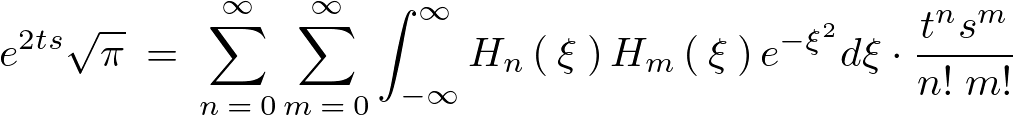
さらにここで、次のような指数関数の和の形への変換、
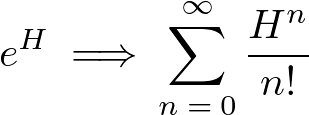
を思い出せば、次のような式変形ができます。
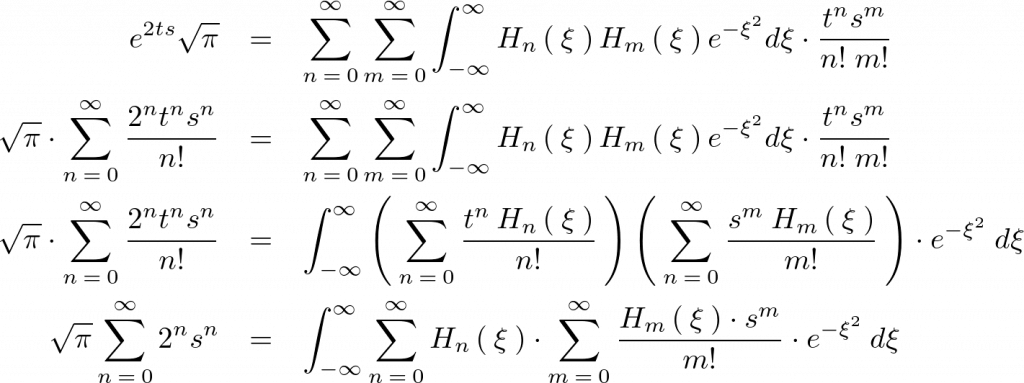
ここでいったん上記式に関しての直交性を確認するために和の記号を取り外して次のように式を置きます。
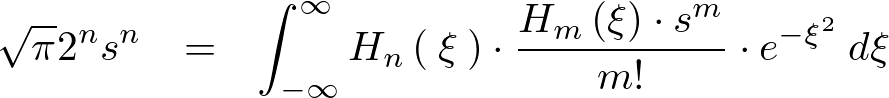
エルミート多項式の直交性の確認
上記式が成立する条件を考えます。
今仮に![]() だとすれば、
だとすれば、
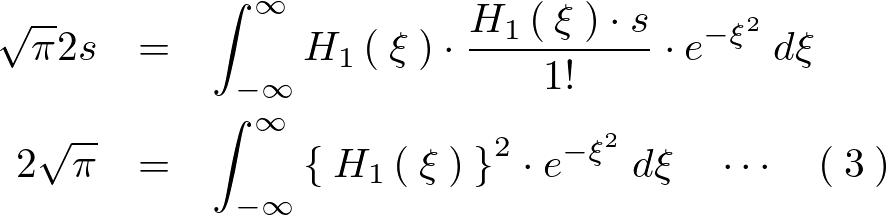
ここで次のようなロドリーグの式を思い出せば次のようなものになります。
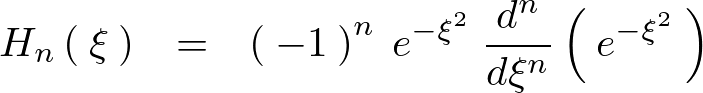
上記の公式に先ほどの![]() を代入して計算すると、
を代入して計算すると、
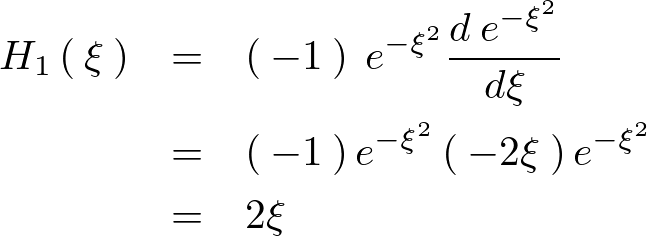
となるので、
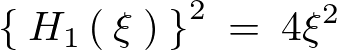
これを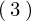 式に代入すると、
式に代入すると、
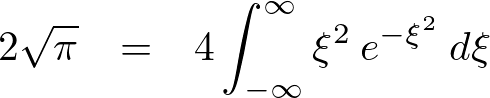
ここで次のようなガウス関数に関する公式をまず最初に明示しておきます。
ガウス関数に関しては次のような公式が存在します。
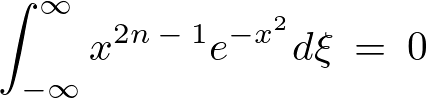
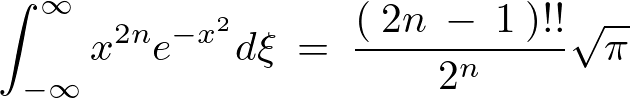
なお下の式の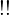 はLaTeXコードの打ち間違いではなく2重階乗(double factorial)というものになります。
はLaTeXコードの打ち間違いではなく2重階乗(double factorial)というものになります。
上記の公式により偶数のみの計算をしていきます。
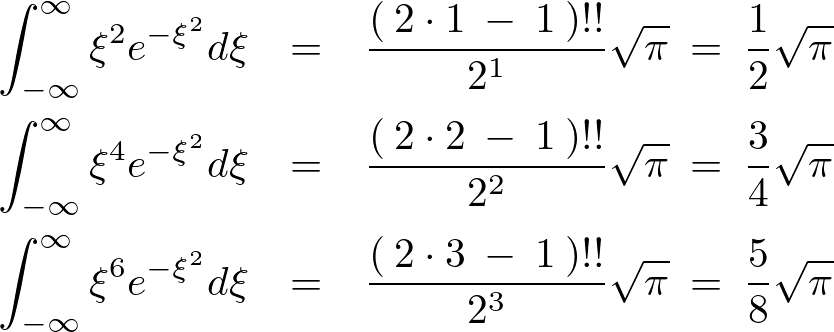
上記3式の一番上の公式より、

となるので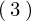 が成り立ちます。
が成り立ちます。
次に![]() のときについて、
のときについて、



 の公式より、
の公式より、

この式により右辺に関しては、

一方上記式の最初のほうの左辺に関しては、

となるので![]() の場合、以下の次式が成り立ちます。
の場合、以下の次式が成り立ちます。

次に のときはどうなるかを考えます。
のときはどうなるかを考えます。
先ほどのロドリーグの式、
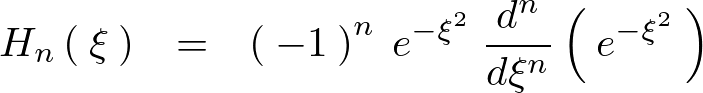
これを使って以下のように式を変形していきます。
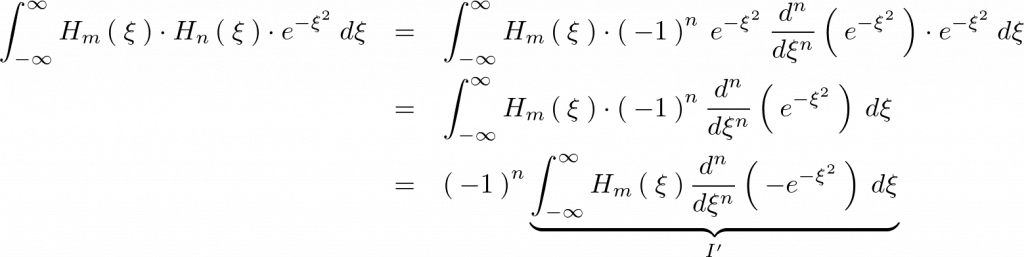
上記式の の部分を部分積分を使って計算していきます。
の部分を部分積分を使って計算していきます。
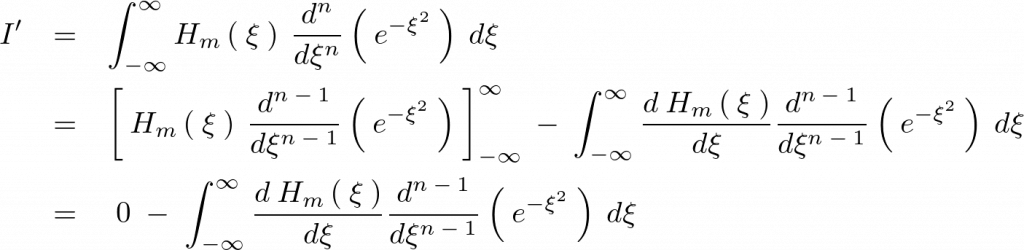
ここでいったん次の公式、
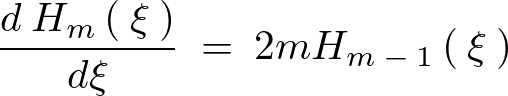
を使うと、
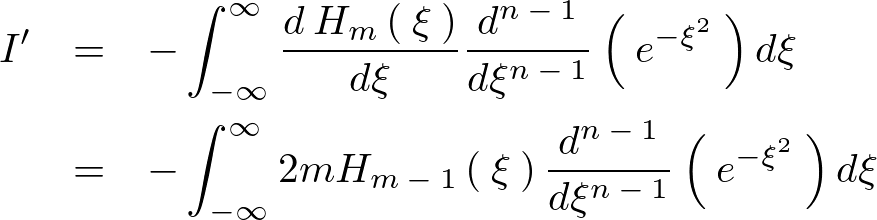
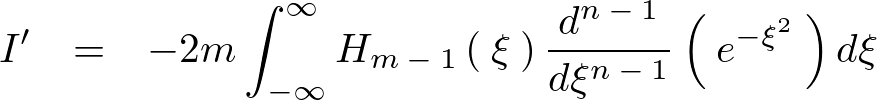
代入し元に戻すと、

次に同様にして上記式の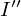 の部分を計算していきます。
の部分を計算していきます。

より次のように求まります。
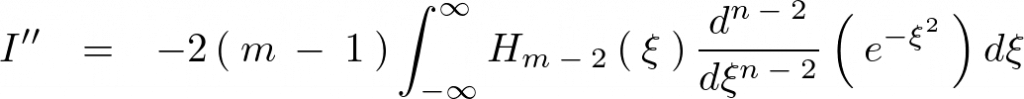
結局のところ上記過程式の繰り返しになります。
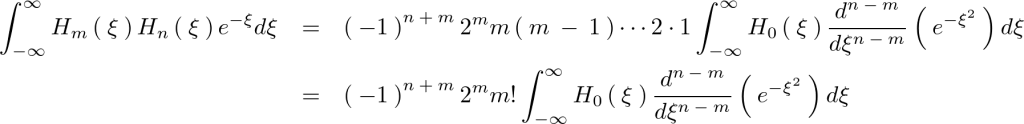
ここで上記式の は、
は、
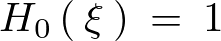
であるので、
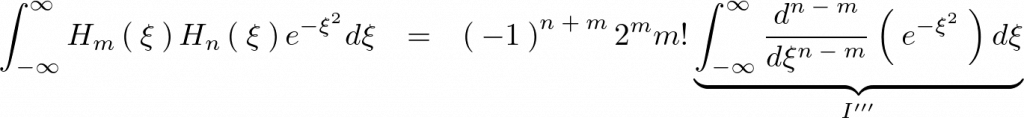
さらに上記式の に関して、微分の回数は最後に
に関して、微分の回数は最後に になるので結局のところ上記式の
になるので結局のところ上記式の に関しては次のような計算式になることになり結局のところ次のように最終的な計算結果として
に関しては次のような計算式になることになり結局のところ次のように最終的な計算結果として になることになります。
になることになります。
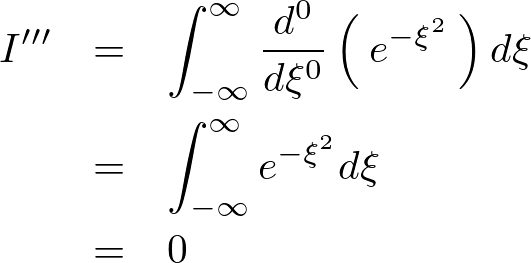
よって のとき次のような関係式が導かれます。
のとき次のような関係式が導かれます。
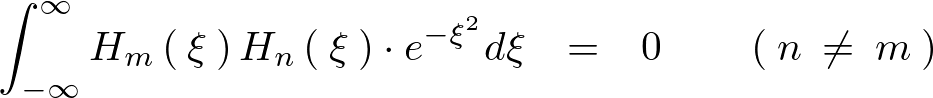
以上をまとめると、![]() のときは
のときは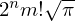 が成り立ち
が成り立ち のときはすべてにおいて
のときはすべてにおいて となるので次に示すようなエルミート多項式は直交性があることが示されます。
となるので次に示すようなエルミート多項式は直交性があることが示されます。

-

ラプラス変換
続きを読む
-
2024年6月8日マイグレーション完了
続きを読む
-
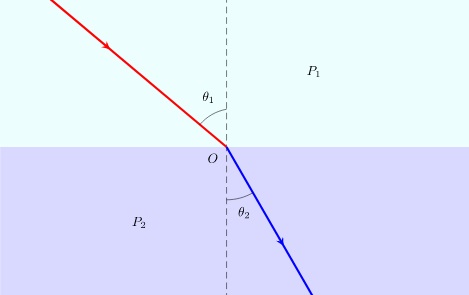
フェルマーの原理
続きを読む
-
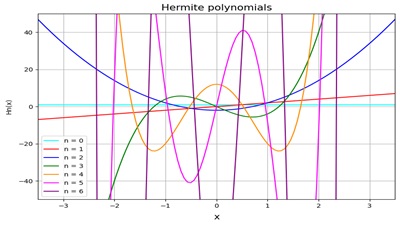
エルミート関数
続きを読む
-
フーリエ余弦正弦展開
続きを読む
-
フーリエ変換
続きを読む