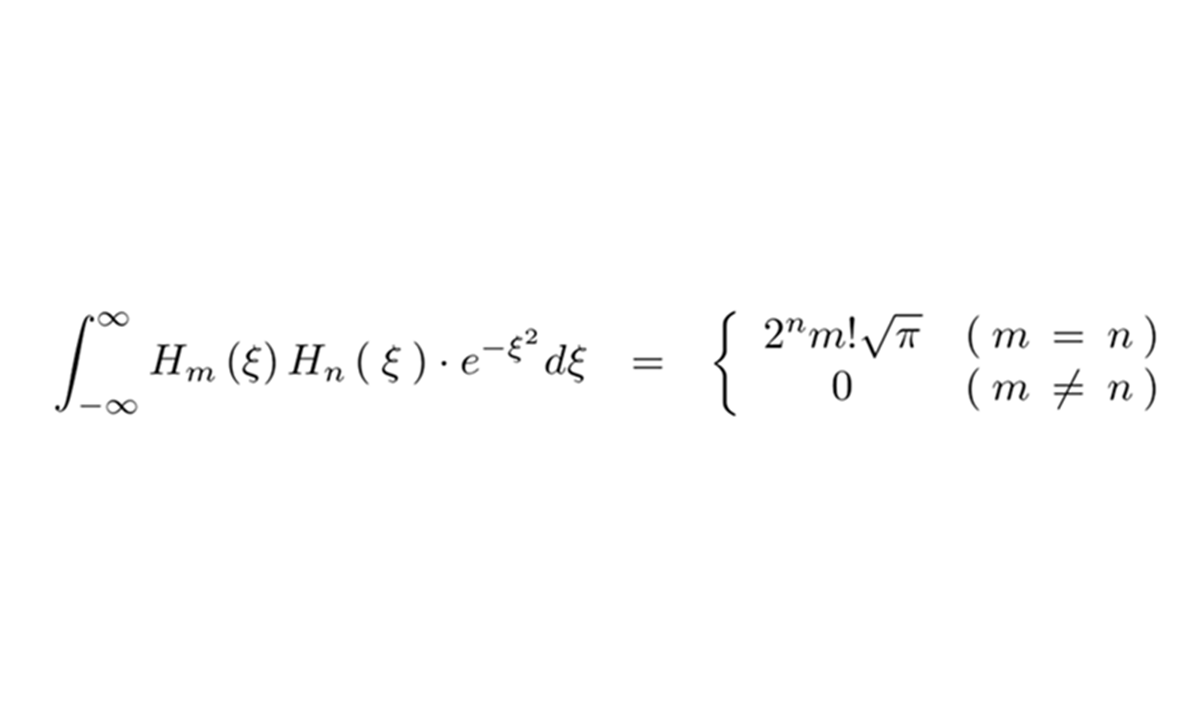エルミート関数とは

エルミートの微分方程式

エルミート関数とは、おもに以下に示すような常微分方程式、

を満たすエルミート多項式のことを指します。

これはスツルム-リウヴィル型微分方程式の一つであり、物理学や数学で重要な役割を果たしています。

エルミート多項式

エルミート多項式の定義式は以下のようなものになります。

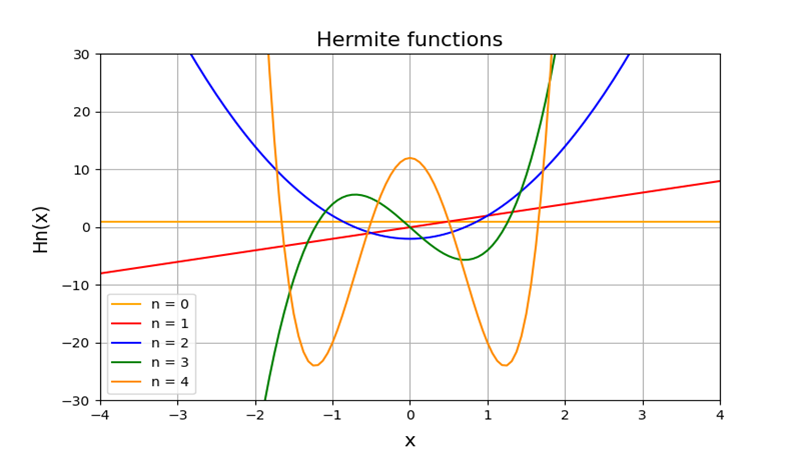
エルミート多項式の視覚化

上記多項式に0から6までの値を次々に代入していきます。

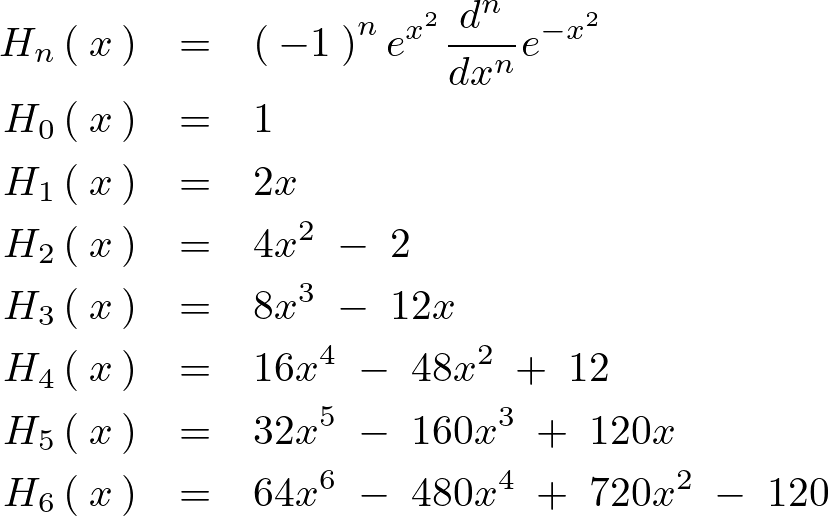
このような結果が得られそれを描画するとこのようになります。

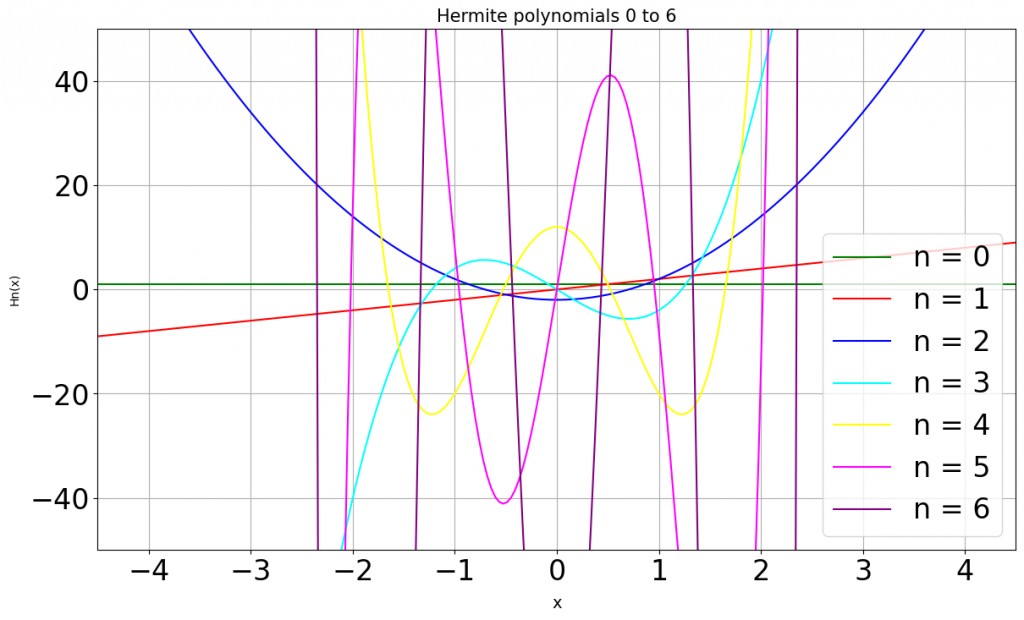
代入する値が大きければ大きいほどその形が複雑になっていくのがわかります。

エルミート母関数

エルミート母関数に関しては以下になります。

この式からエルミート微分方程式とエルミート多項式の一般項を導いていきます。

エルミート微分方程式の導出

上記のエルミート母関数、

この式の両辺をで微分します。

指数部分に関しては以下のように関数を分けて連鎖率を適用してそれぞれを微分していきます。

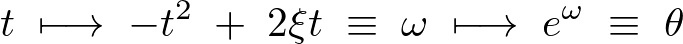
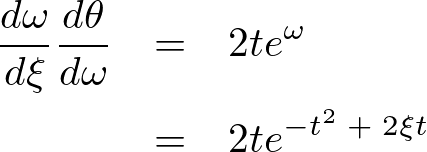
これより級数を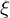で一階微分したものは以下のようになります。

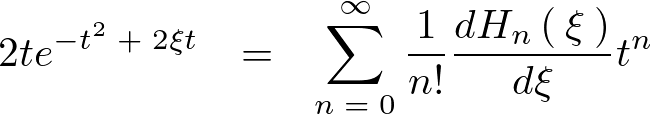
上記をさらに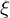で微分します。先ほどと同様にして関数を分けて連鎖律を適用して微分すれば以下のようになります。

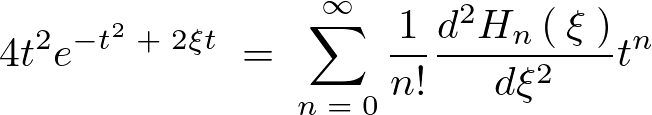
今度は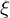ではなくで微分します。

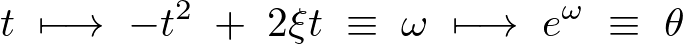
同様にして連鎖律を適用します。

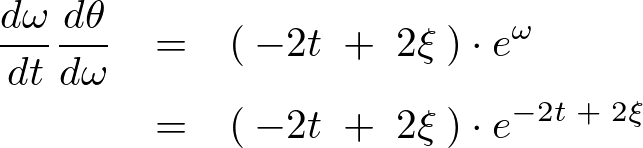
以下のように求まった式の両辺にを掛けます。

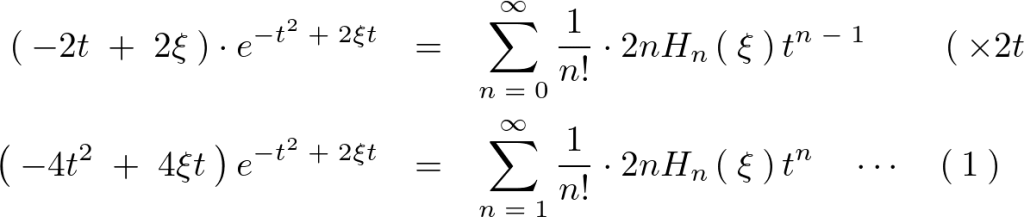
先ほどの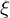で微分した式の両辺に対して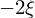を掛けます。

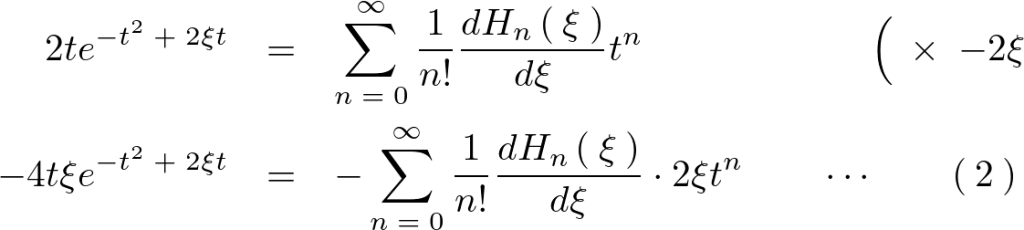
ここで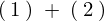として辺々足し合わせます。

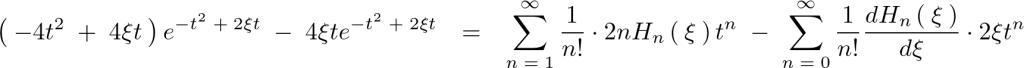
ここで、

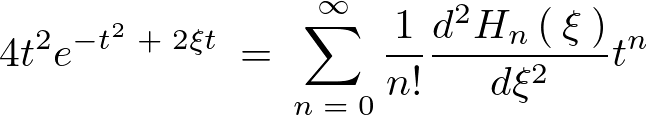
だったのでこれを代入します。

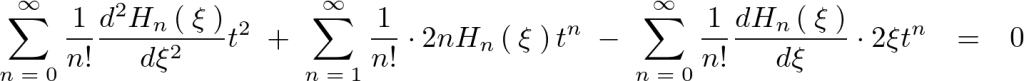
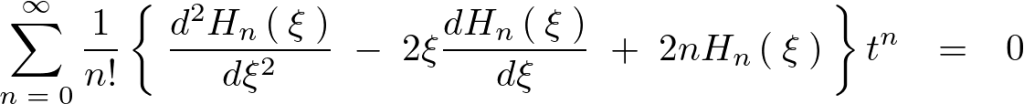
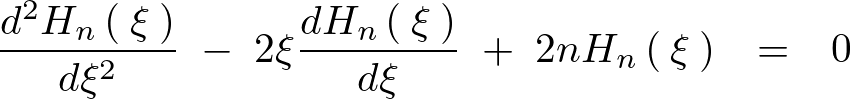
でくくって整理すれば以下のような微分方程式が求まります。

エルミート多項式の一般項の導出

先ほどのエルミート母関数の左辺を以下のように変形していきます。

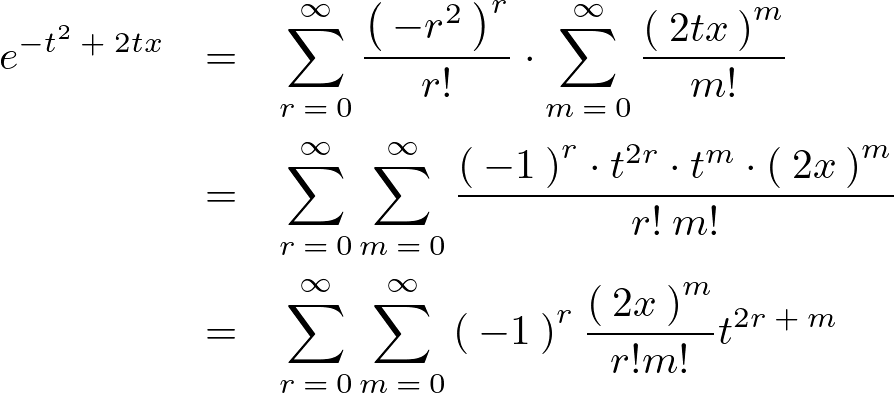
ここで次のようにおきます。

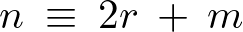
これを代入すると、

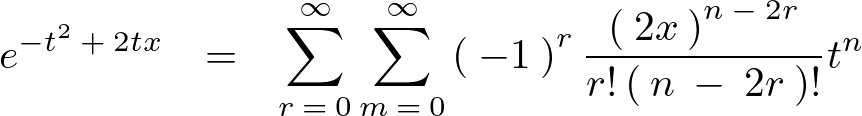
また上記とすればは以上であるためという関係式が成り立ちます。床関数をと表して以下のように偶数と奇数に分けます。

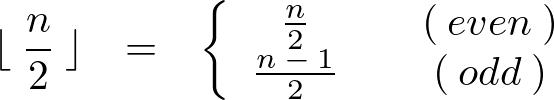
これを使ってはから始まるものとすれば以下のようになります。

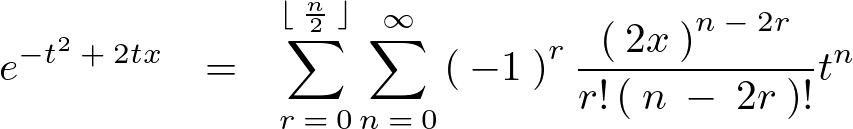
参考：https://en.wikipedia.org/wiki/Hermite_polynomials

元の式に代入します。

整理すれば以下のようなエルミート多項式の一般項が求まります。

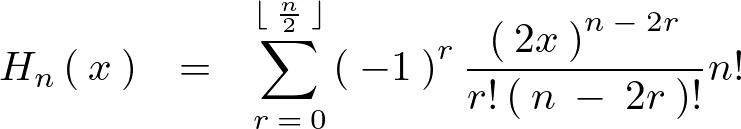
漸化式

解として以下のようなものを仮定します。

これを1階、2階と微分していきます。

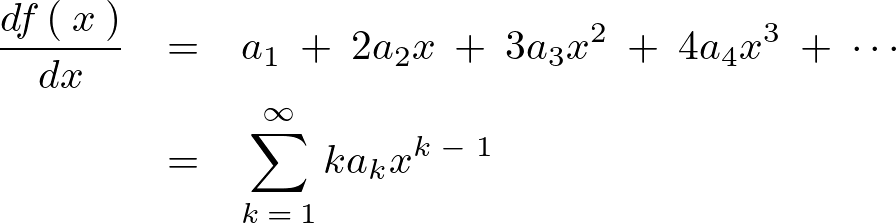
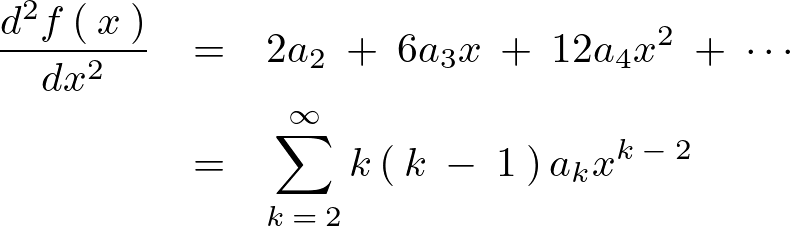
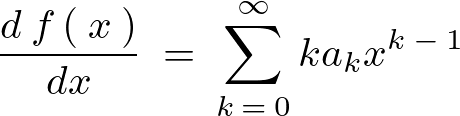
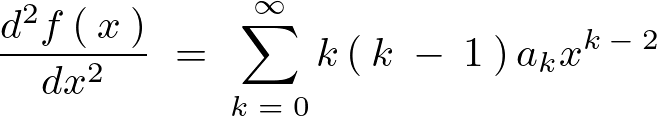
このカテゴリーではエルミート多項式全般に関してその主な振る舞いを考察していきます。