ベッセルの微分方程式とは
ヘルムホルツ方程式と呼ばれる式に対し、円柱座標を適用させて得られる方程式に次に示されるような微分方程式があります。
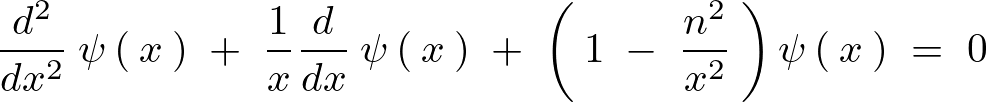
この微分方程式の解を導くためには普段通りのやり方だとうまくいかないので、ある級数を一つの解として仮定するやり方─“級数解法”という方法を使ってその解を求めていくことになります。
以下のような級数を置きます。
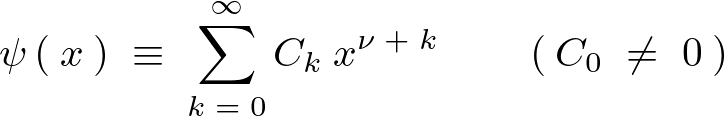
これを以下のように1階、2階と微分していきます。
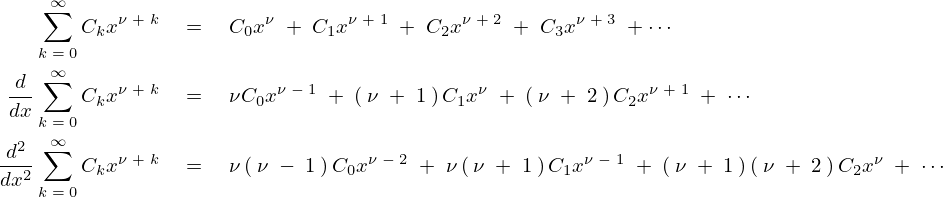
まとめれば次のように表現できることになります。

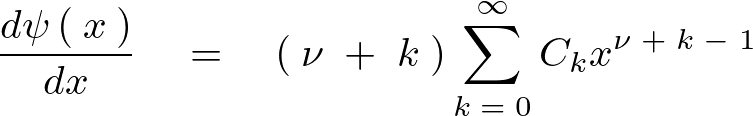
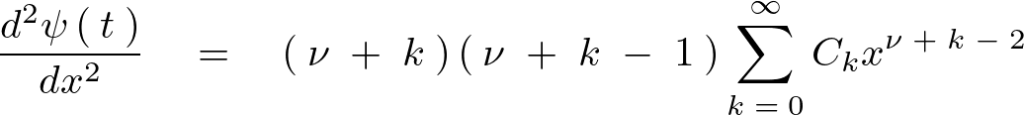
これらを先ほどのベッセル微分方程式の中にそれぞれ代入していきます。
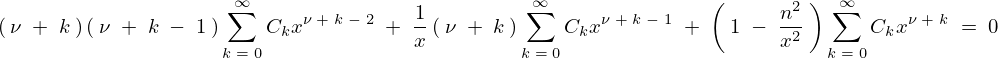
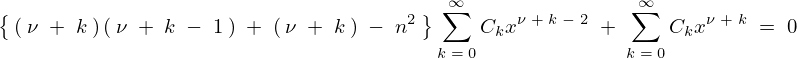
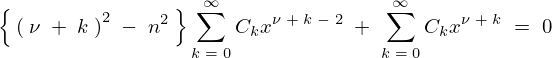
ここで上記式の左辺第1項を次のように分けて考えていきます。
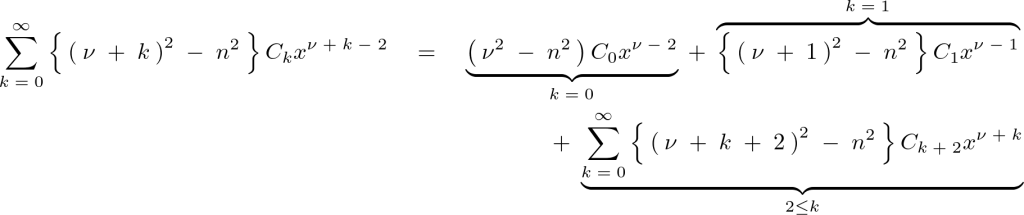
より、

第一項から、
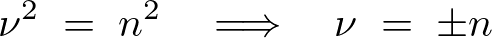
左辺第2項から![]() を考慮すると、
を考慮すると、
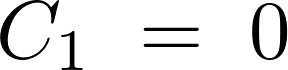
さらに第3項から、
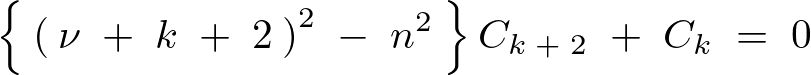
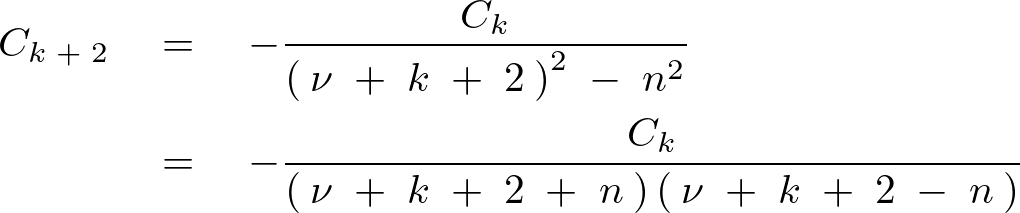
ここで式のなかの![]() を
を![]() と同じ正の実数と考えて次のようにします。
と同じ正の実数と考えて次のようにします。

これにより次のようになります。
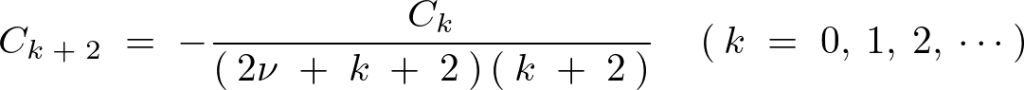
![]() を
を![]() より順に代入していきその式の変化を見ていきます。
より順に代入していきその式の変化を見ていきます。
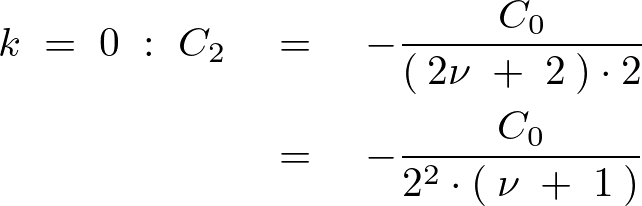
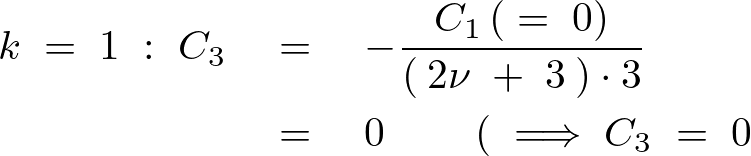
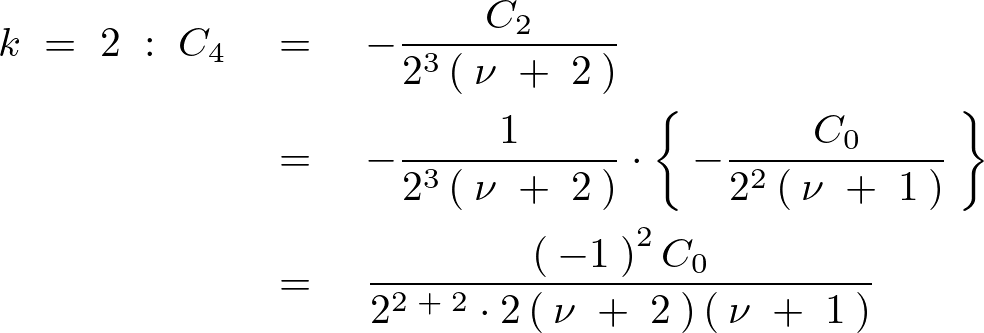
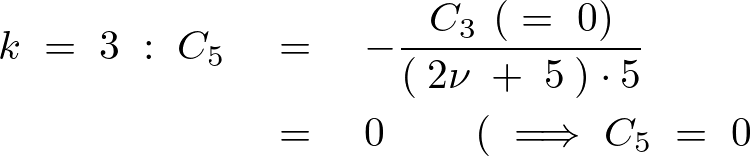
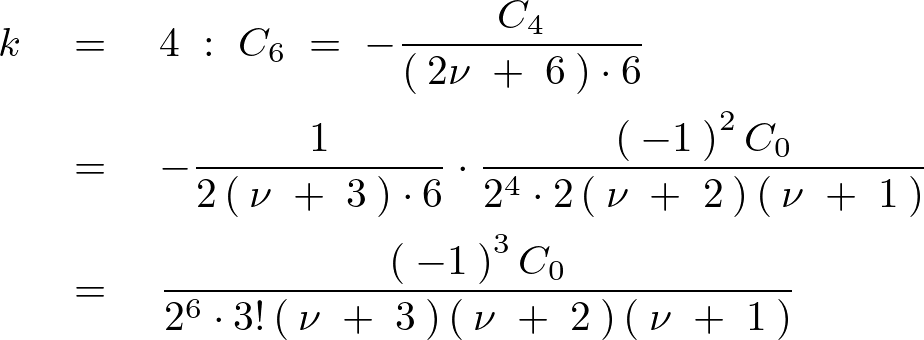
こうした結果により奇数項は![]() になるのでこれを省くために新たに
になるのでこれを省くために新たに![]() というのを用意して次のようにしていきます。
というのを用意して次のようにしていきます。
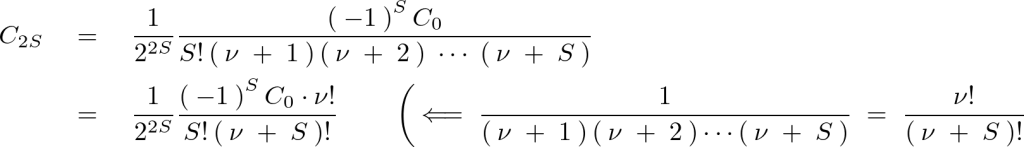
式の中の![]() を次のように置きます。
を次のように置きます。
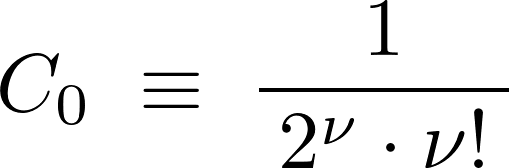
これにより、
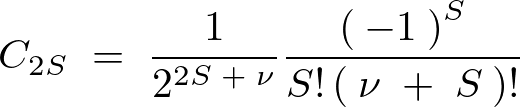
最初の式に当てはめれば、
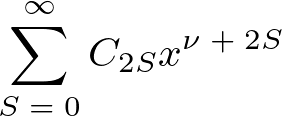
となり解と仮定したべき級数は次のようにおけます。
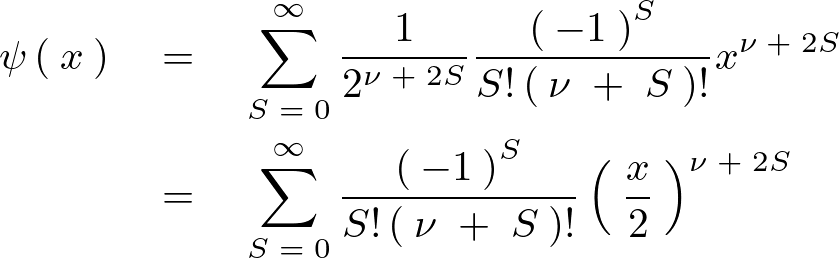
さらに次に示されるような性質を持つガンマ関数と呼ばれるもの、
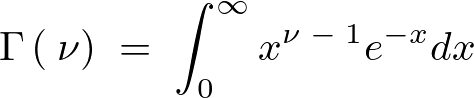
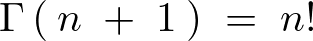
こうした性質を持つガンマ関数を利用し、さらにを![]() 用いて最終的に次のような関数が求まります。
用いて最終的に次のような関数が求まります。
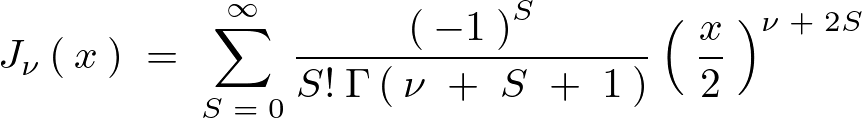
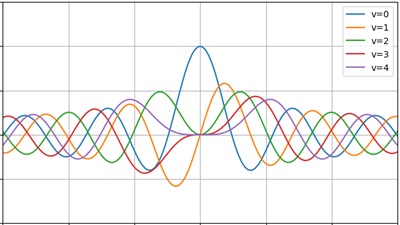
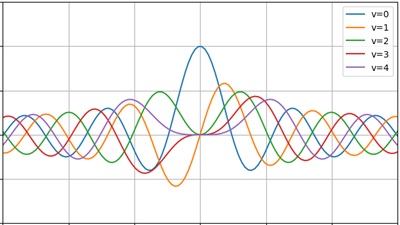
ベッセル関数の描画
いろいろな値を代入したベッセル関数をグラフにするとこんな感じになります。



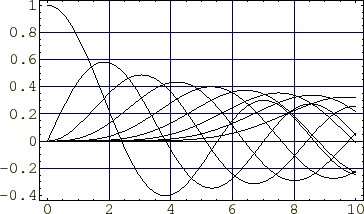
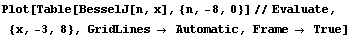
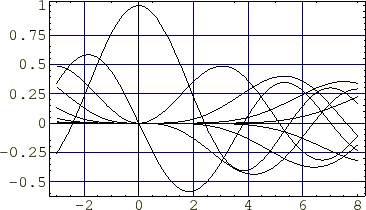

ベッセルとガンマ関数
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.