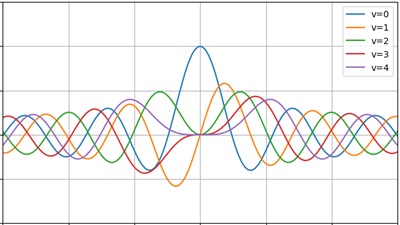
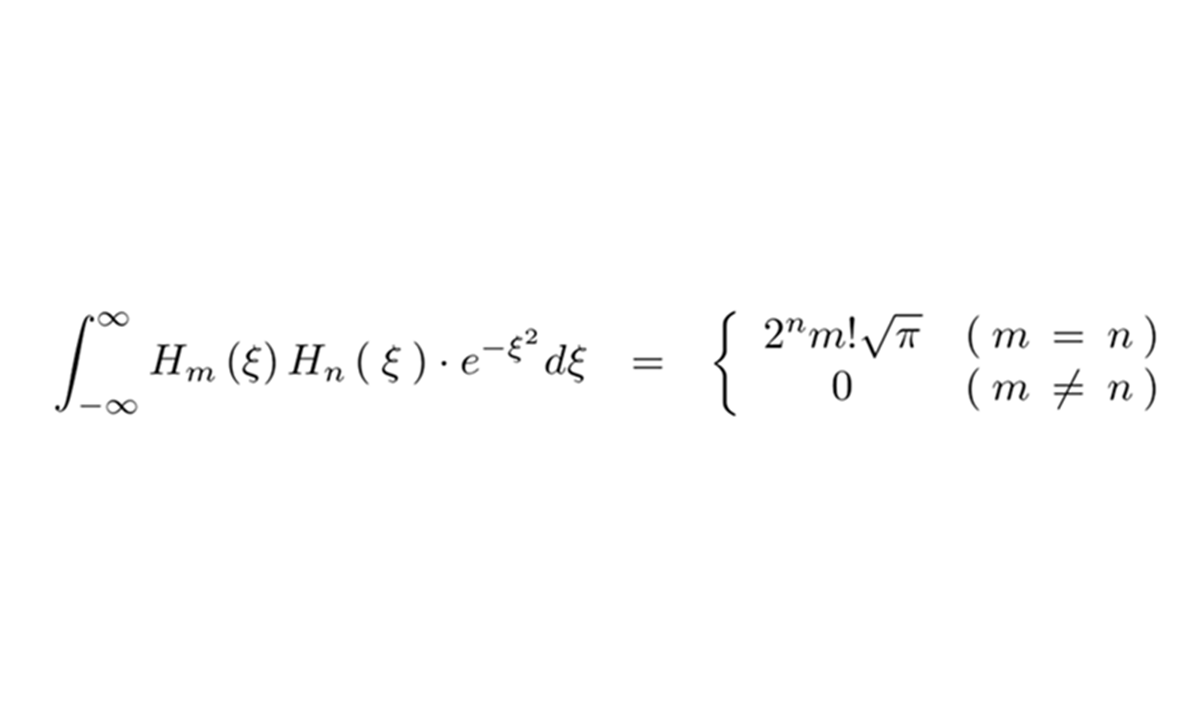特殊関数とは

特殊関数とは、解析学、物理学、関数解析学その他の応用分野でよく使われる関数であり、特殊な名前や記法が定着しているものになります。

ガンマ関数（Gamma function）、ベータ関数（Beta function）などからはじまって、ルジャンドル関数（Legendre function）、ベッセル関数（Bessel function）、ゼータ関数（Zeta function）、楕円関数（Elliptic function）、超幾何関数（Hypergeometric function）、それ以外にも直交多項式（Orthogonal polynomials）などと呼ばれるラゲール多項式やエルミート多項式などがあります。

◆コンテンツ紹介

ベッセル関数

ベッセル微分方程式の導出

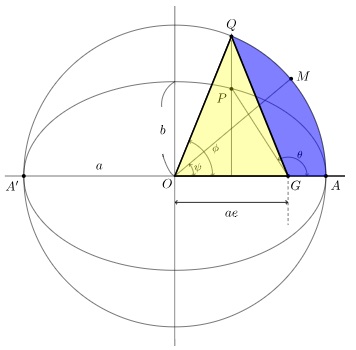
上記の微分方程式をベッセルの微分方程式といいます。もともとは天文学者ベッセルによる惑星の軌道運動の考察研究から始まったもののようですがその後の数学者や物理学者たちによって様々な物理現象を解明するに至ったという背景があり、そのためそれらに関連するものも含めてベッセル関数と呼ぶようになったようです。ベッセル関数はヘルムホルツ方程式やラプラス方程式に対して、円筒座標系や極座標系などを適用した場合の分離解として応用され、例えば薄い円形膜の振動の解析などに利用されます。このセクションでは惑星の運動軌道を説明するケプラー方程式から第1種ベッセル方程式を導くまでの過程に関して考察していきます。

ベッセル微分方程式の解

ベッセルの微分方程式の解を導くためには普段通りのやり方だとうまくいかないので、ある級数を一つの解として仮定するやり方─“級数解法”という方法を使ってその解を求めていくことになります。

以下のような級数を置きます。

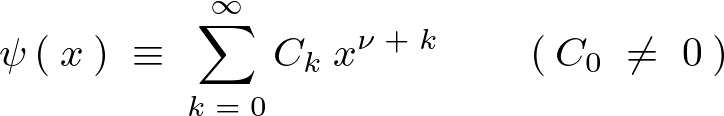
この解とみなした級数を１階、２階と微分していけば次のような級数展開が導かれることになります。

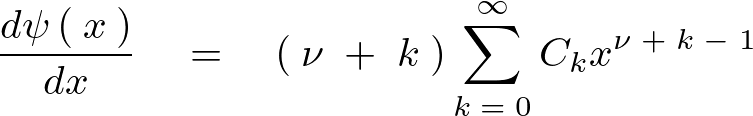
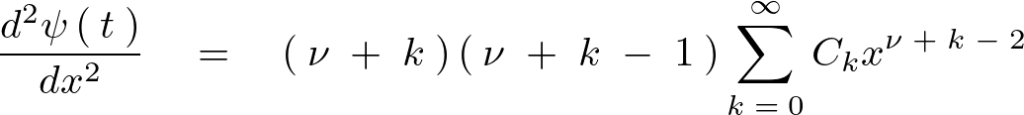
これらを利用して先ほどのベッセルの微分方程式の解を導いていきます。

エルミート関数

エルミートの微分方程式

エルミート関数といえば一般的にエルミート多項式のことを言います。アルファベット表記は、Hermiteになりハーミットとは呼ばずエルミートと呼びます。ラテン語読みでそうなります。

式としては以下のような常微分方程式になります。

これはスツルム-リウヴィル型微分方程式の一つであり、現在においては物理学や数学で非常に重要な役割を果たしています。

エルミート多項式

エルミート多項式の定義式は以下のようなものになります。

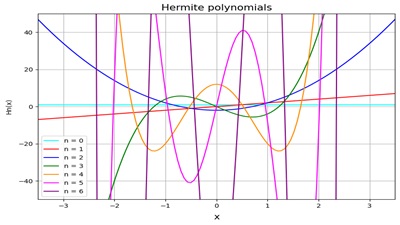
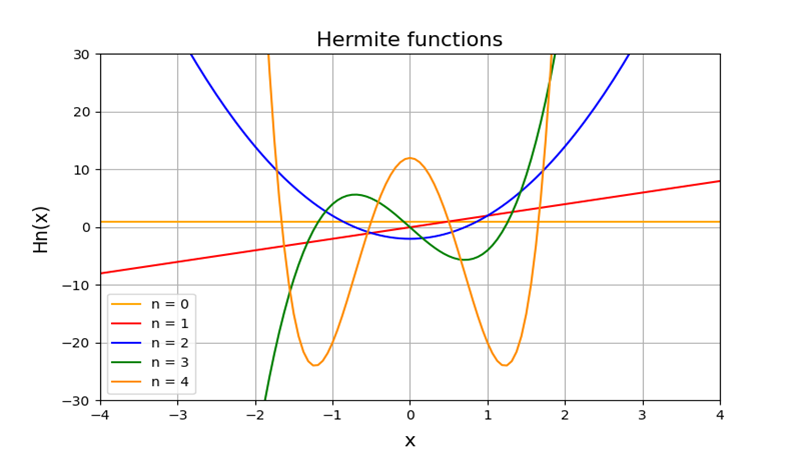
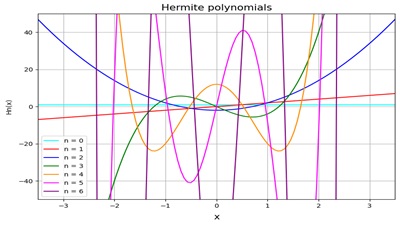
上記多項式に0から6までを代入していった場合次のようなになります。

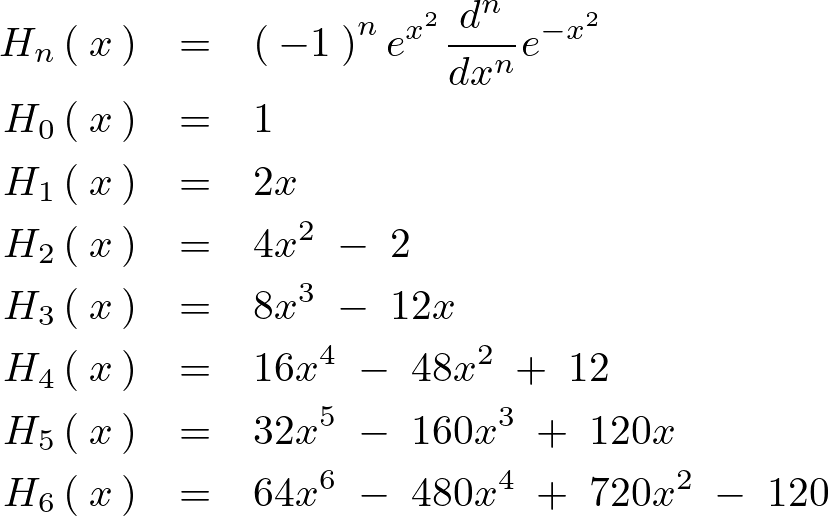
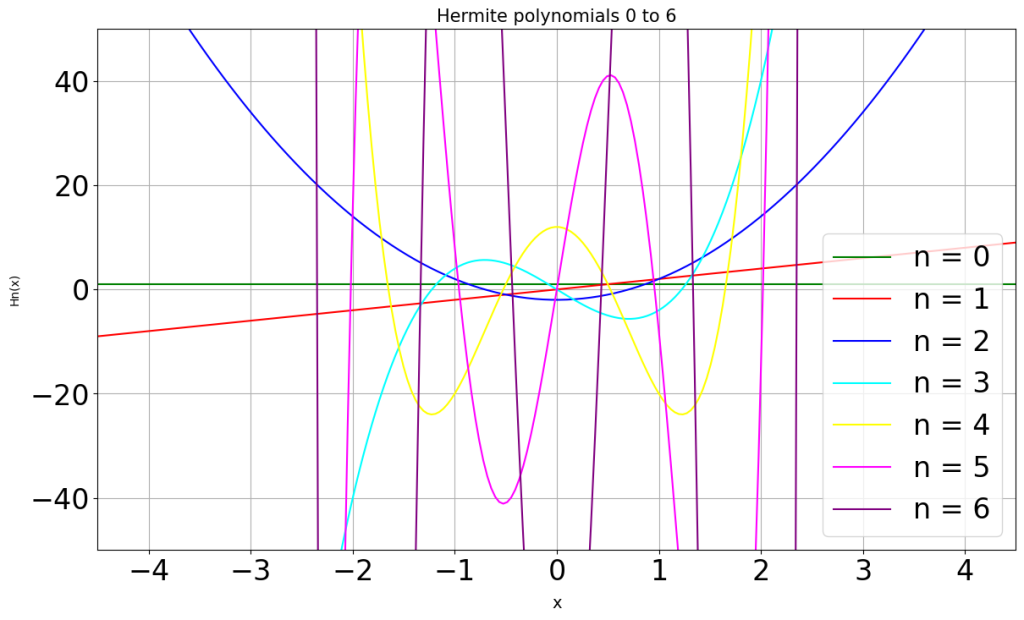
このカテゴリーでは量子力学などにおいて大変重要な立ち位置にあるエルミート関数に関して考察していきます。