一次元調和振動子とは
シュレーディンガー方程式における一次元調和振動子の挙動
力学の分野において理想的なバネにつながれた物体の振動する様子を示したものを一般的に調和振動子などと言ったりしますが、その調和振動子に量子力学においてよく出てくるシュレーディンガー方程式という式に当てはめていった場合、数式的にどのような振舞を示すかを考察します。
以下がいつもよく見かけるシュレーディンガー方程式になります。
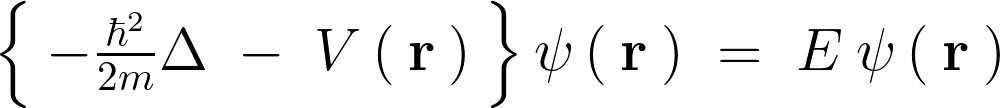
シュレーディンガー方程式と呼ばれるものは上に示すようなものでした。
ここで一次元調和振動子におけるポテンシャルエネルギー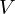 を次のように置きます。
を次のように置きます。
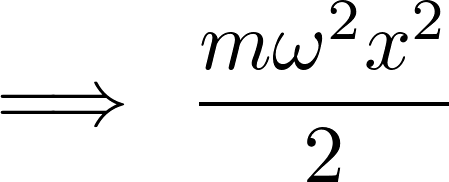
こうすると先に挙げたシュレーディンガー方程式は次のような形になります。
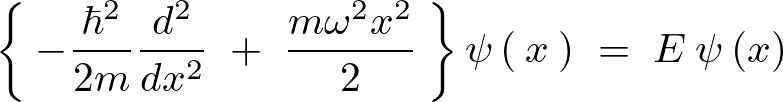
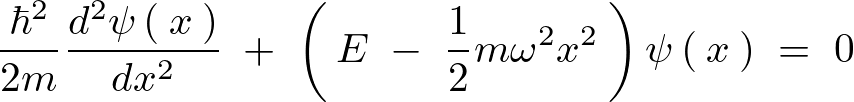
この微分方程式を解くために座標![]() の代わりに
の代わりに![]() を使って変数変換し
を使って変数変換し![]() を用いて
を用いて![]() を次のように置きます。
を次のように置きます。
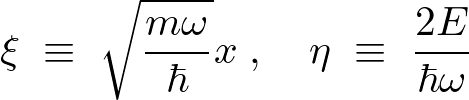
一次元調和振動子におけるシュレーディンガー方程式の解を求めます。 作用素をチェーンさせ作用素そのものを変化させます。
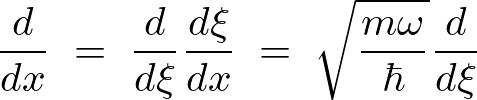
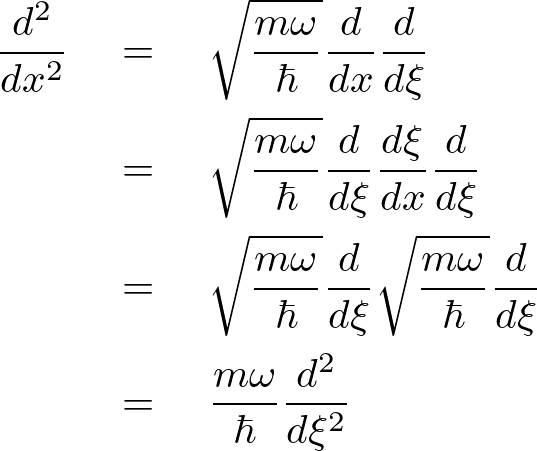
これにより2階の作用素は次のように変形できます。
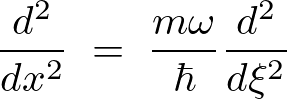
これらの結果を使って先ほどのシュレーディンガー方程式を変形させていきます。
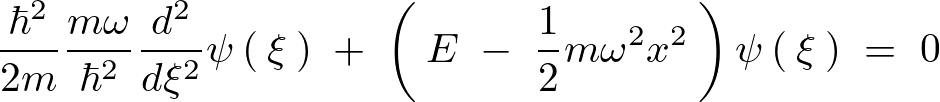
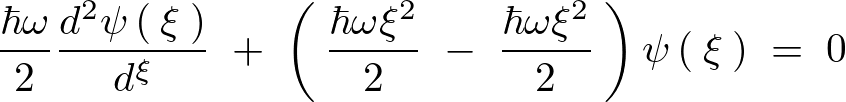
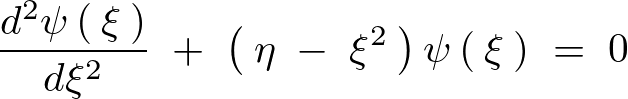
といった具合で最初に出てきたシュレーディンガー方程式は、上に示されるような形に変形させた微分方程式が出てきます。
ベキ級数による級数解法
これの解を求めていくのですが通常のやり方でいくとうまく解が求まりません。そこであるベキ級数を解と仮定する“級数解法”というやり方をしていってこの微分方程式を解いていきます。
解と仮定した![]() を次のように置きます。
を次のように置きます。
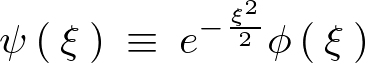
これを次々に微分していきます。
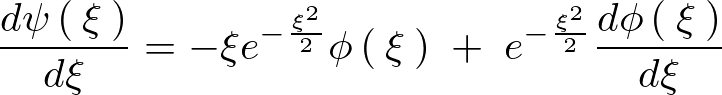
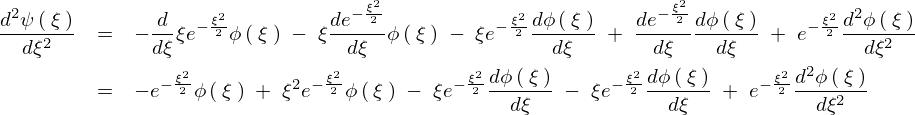
代入していきます。
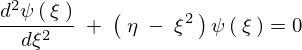
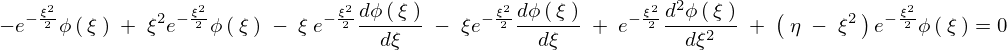
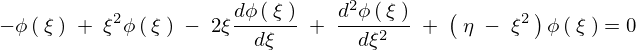
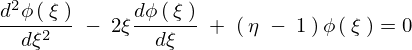
以下のように求まります。
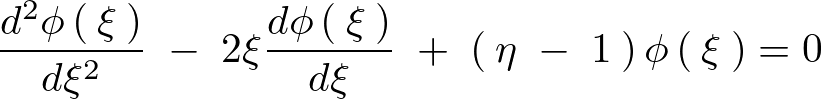
ここでこれの解を次のように置きます。
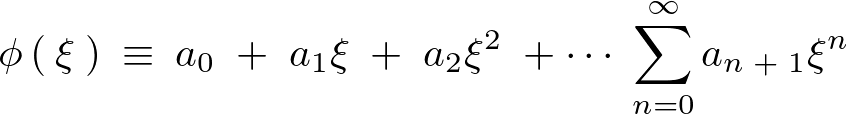
こうすることにより、微分していけば、
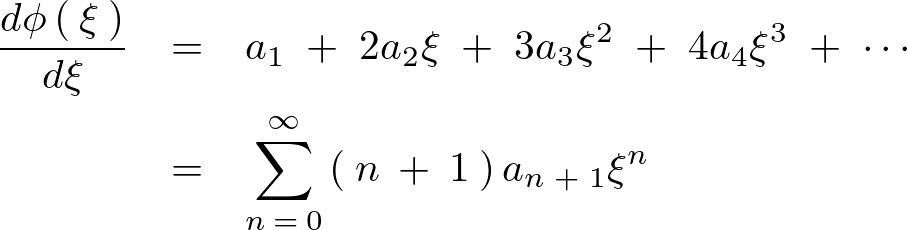
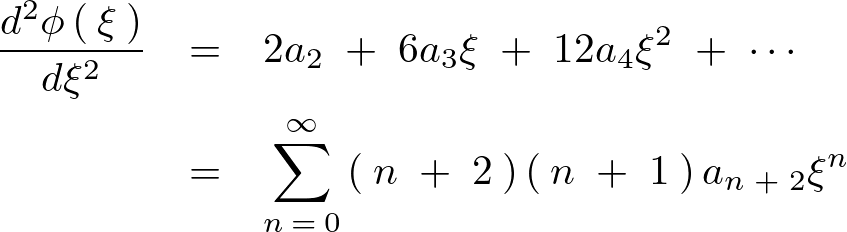
よって、
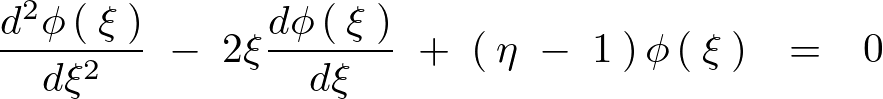
の式は次のようになります。
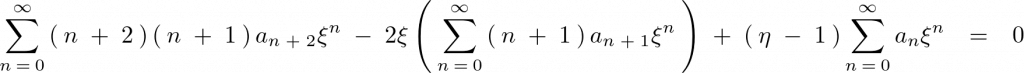
さらに変形していきます。
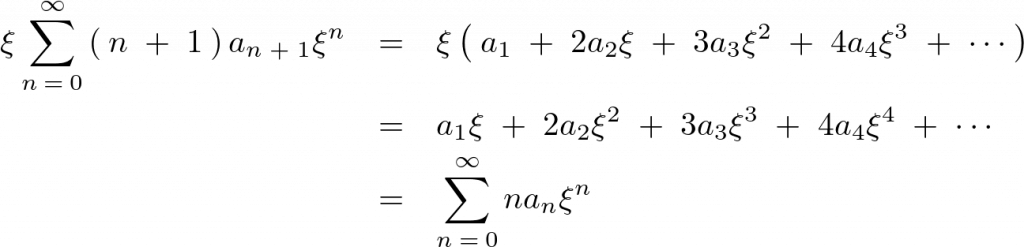
代入してまとめます。
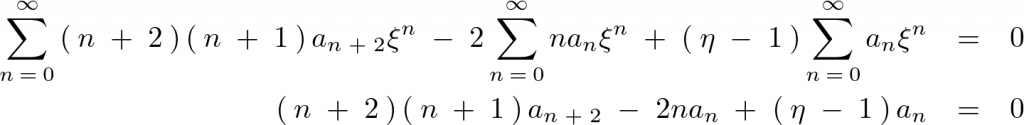
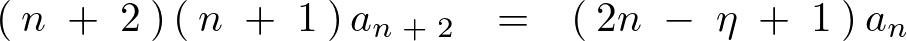
整理すると次のような関係式が求まります。
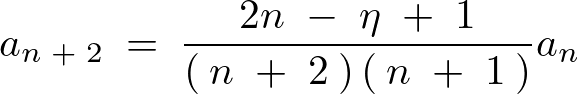
これらの結果により分子のほうで![]() という条件を付けると
という条件を付けると![]() はゼロになり
はゼロになり![]() は収束します。
は収束します。
![]() によって
によって![]() が決定されることになりますがこれが発散しないようにすればよく、
が決定されることになりますがこれが発散しないようにすればよく、![]() で
で![]() となるために
となるために![]() 。これより、
。これより、
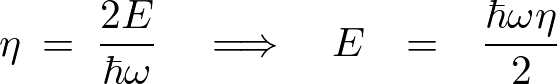
より、
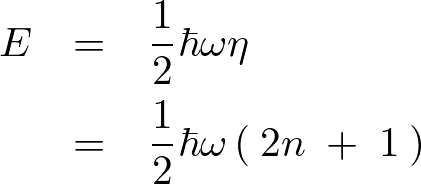
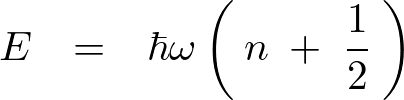
この結果によって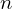 は
は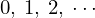 のように続くのでエネルギー単位
のように続くのでエネルギー単位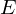 は
は![]() ごとの均等なレベルで表示されることになります(連続ではなく飛び飛びのものとして奇妙な扱われ方をするということを意味している)。
ごとの均等なレベルで表示されることになります(連続ではなく飛び飛びのものとして奇妙な扱われ方をするということを意味している)。
-
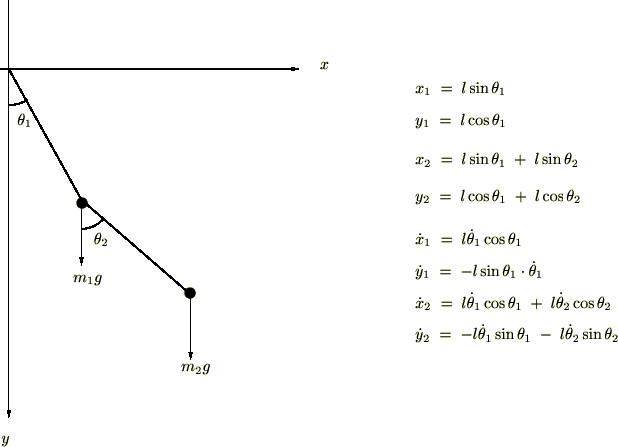
2重振り子②-微小でない場合
続きを読む
-
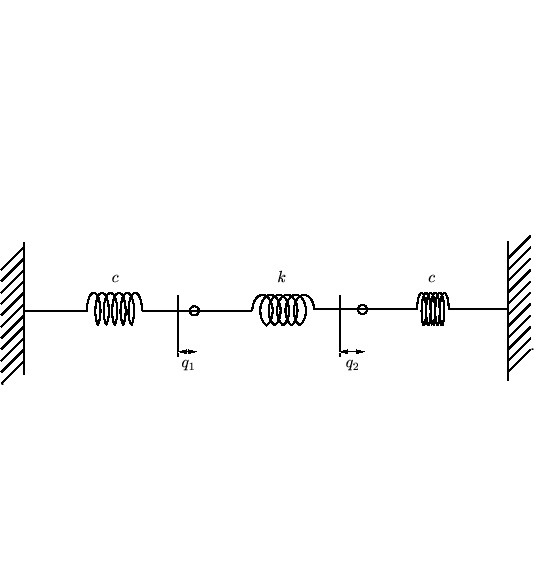
連成振動の解②━3重ばねの振動
続きを読む
-
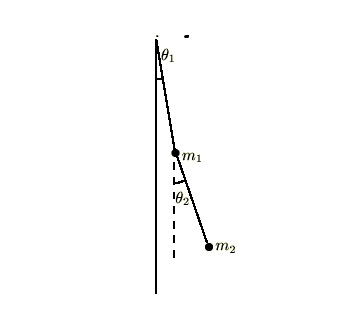
2重振り子①-微小な場合
続きを読む
-
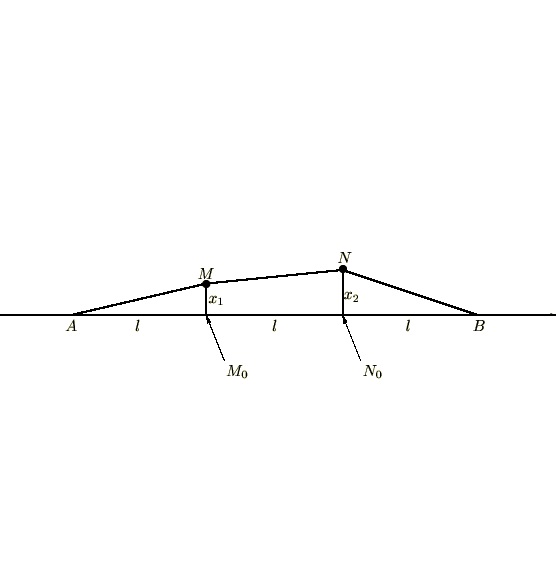
連成振動の解①━弦の振動
続きを読む
-

ヘヴィサイド演算子法
続きを読む
-
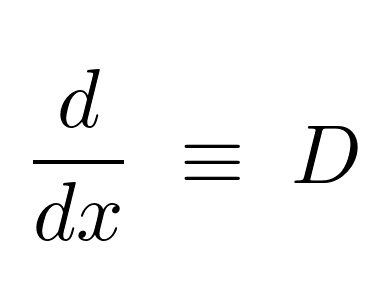
微分演算子による連立微分方程式の解法①
続きを読む
-
-
-
-
2024年6月8日マイグレーション完了
カテゴリー : 2024年6月8日マイグレーション完了diff-eq.comのドメインを取得してから約1年がたち、今年の3月末から本格運用を開始していたが、Cent…
-
-
-
-
-
-