量子力学
量子力学とは
量子力学 ━ 佐野量子の量子と書いてりょうしりきがくと読みます。漁師力学ではありません。近代に入ってから発展してきた現代物理学のことを一般的に差し、通常(正統派)の物理学を古典物理学などと言ったものに対比して対照的な表現として用いられることもあるようです。
その振る舞いは通常の物理学の考えとは一線を画した量子状態といえるものになり、難解な数学によって無理くりにその因果律を求めてきたという感じのものになります。どのような無茶ぶりかというと、例えば、道端に一本の小枝が落ちていたとします。この小枝が真直線であり、さらには地球そのものが真球であったとします。小枝の始点をA、終点をBとした場合、始点Aをずっと伸ばしていった場合、その始点Aはいづれ地球をぐるっと回って終点のBにたどり着くはずです。それがそうならない理由を数学的に証明しろ、と言っているような学問になります。こうしてたとえてみればいかに量子力学という分野が無茶苦茶な物理学分野であることがわかると思います。ただしこれはあくまで私個人の感覚で言っていることになりますので内容が飛躍した表現であったと思われる場合は、決して語弊を招くためのものではないことを念のため言っておきます。
量子力学を学ぶ上での処世術(みたいなものとは何か)
個人的な話になりますが大学で膜理論を研究している教授がその授業の中で量子力学の話になった際に、「量子力学がわかった、なんて言っているやつは本物のバカだ‼」と言っていたのを今でも強烈に覚えています。あくまで個人的な意見ですが私からすれば量子力学がわかったと言っている人は数学の才能に関して、とりわけ秀でた才能をお持ちの方だと思っています。だから“バカ”などとは一切思っておりませんが、ただもともと古典物理学とは対照的になぜそうなるのかということがそもそも論として全く理解できていない常識はずれな事象に関して、「わかった!」などと言ってる人物に対しては、はっきり言わせてもらうと「ん???」となってしまうのもまた事実になります。
であるために、上記のような理由により、物理が専門でないにもかかわらず量子力学が何たるかを堂々と喧伝するような人間は、物理学をちゃんと学んできたものからすればはっきり言って軽蔑の対象でしかならないということを十二分に認識しておいたほうがよろしいでしょう。
経緯と背景
というわけで上記の理由などによりもともと当Webサイト管理人はあまりこの分野は好きではありません。しかしながら現在においてはかつて不可能と思われていた量子コンピュータなるものが現実的になりつつある状況のなかで、時代が時代だけに私自身が今後業務でかかわってくる可能性がほぼ確実になることは避けられない状況となっているのをひしひしと感じており、そのためそのアウトプット的なものの準備付けみたいなコンテンツとなっています。なのでいまのところドラコンがメインになります。またスラッグに関して、一応量子力学としているので通常であればquantum_mechanicesになるところをquantumになっているのもそうしたことが関係しています。つまり量子コンピュータなどのコンテンツも入れればタイトルは量子力学ではなく量子論にするかそれともそれ以外のタイトルをさらに考えるかかなり迷っている次第になり、ひとまずは“量子力学”としています。今後スラッグの変更はありませんがタイトルのネーミングは変更になるかもしれません。
チャプターカテゴリに関しても全然考えていない状態であり、今後URLも変更になると思うのでプルダウンメニューからなるべく入るようにしてください。
コンテンツ紹介
今のところ予定しているコンテンツに関しては以下のようなものになります。
一次元調和振動子
力学の分野において理想的なバネにつながれた物体の振動する様子を示したものを一般的に調和振動子などと言ったりしますが、その調和振動子に量子力学においてよく出てくる次のようなシュレーディンガー方程式と呼ばれる以下の式、
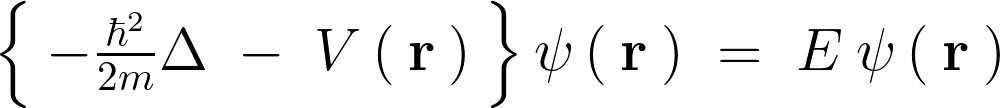
これに当てはめていった場合、数式的にどのような振舞を示すかを考察します。
行列力学によるスピン角運動量合成
電子スピンを合成していった場合の量子力学における角運動量合成に関して議論していきます。
摂動論
惑星運動を計算していった場合に、実際の求めた計算とは微妙に違った軌道を描きます。これはその外側の惑星による引力が原因になって計算によって求められた軌道より少し離れた場所を周回することを言います。これが量子の世界にも当てはまるいことがわかっています。このエントリではこれを扱っていきます。
調和振動子の行列表示
一次元調和振動子で扱った内容でこれを行列を使って考え直してみます。
一次元における反射とその透過に関しての数学的理解
E<V_0であるにもかかわらず持ち合わせているエネルギーを超えた山形ポテンシャルのトンネル効果による透過現象に関して理論的な解釈によって考察していきます。
-
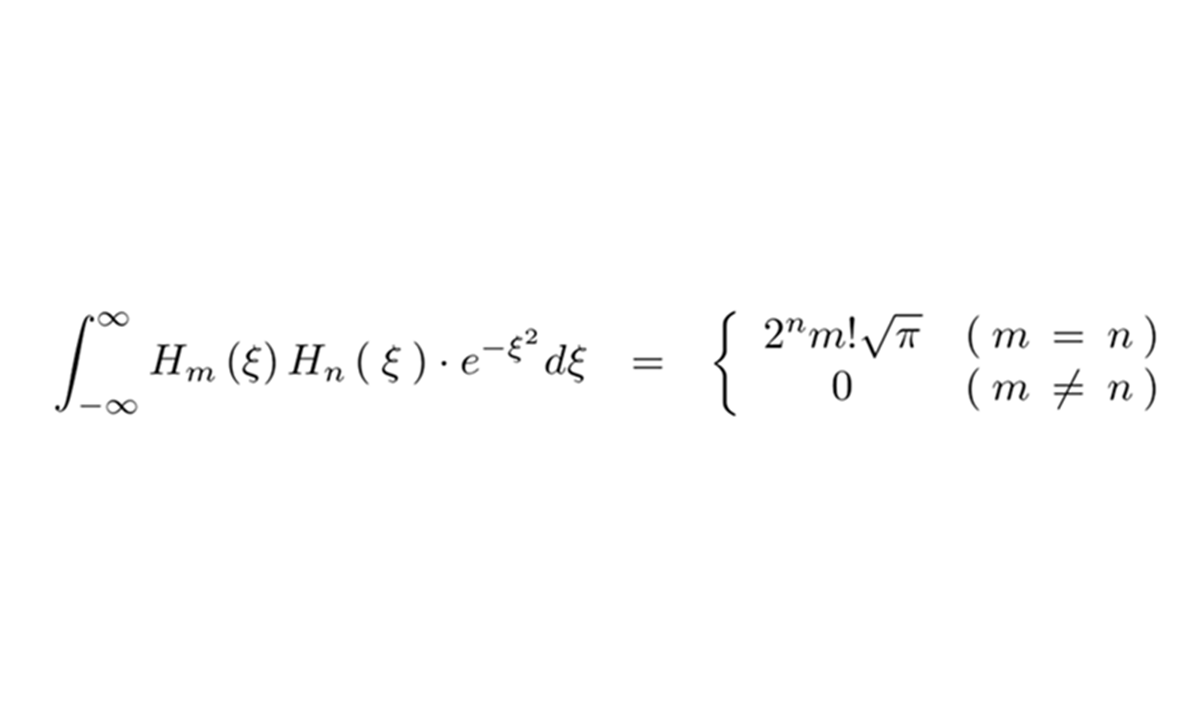
エルミート多項式の直交性
続きを読む
-
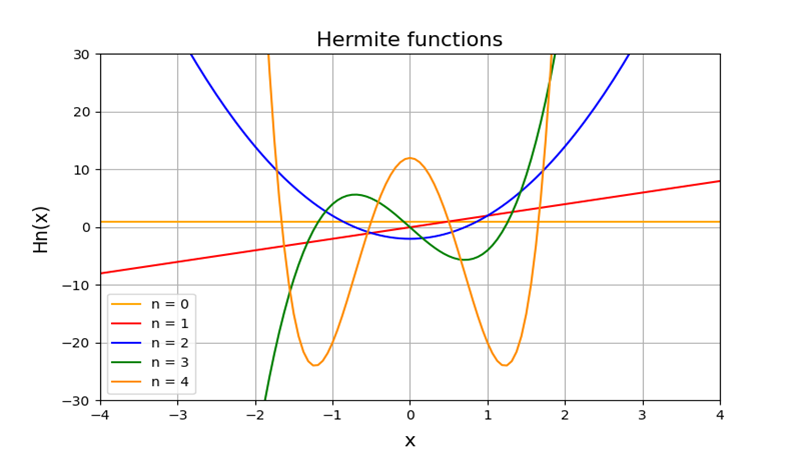
エルミート多項式の諸性質
続きを読む
-
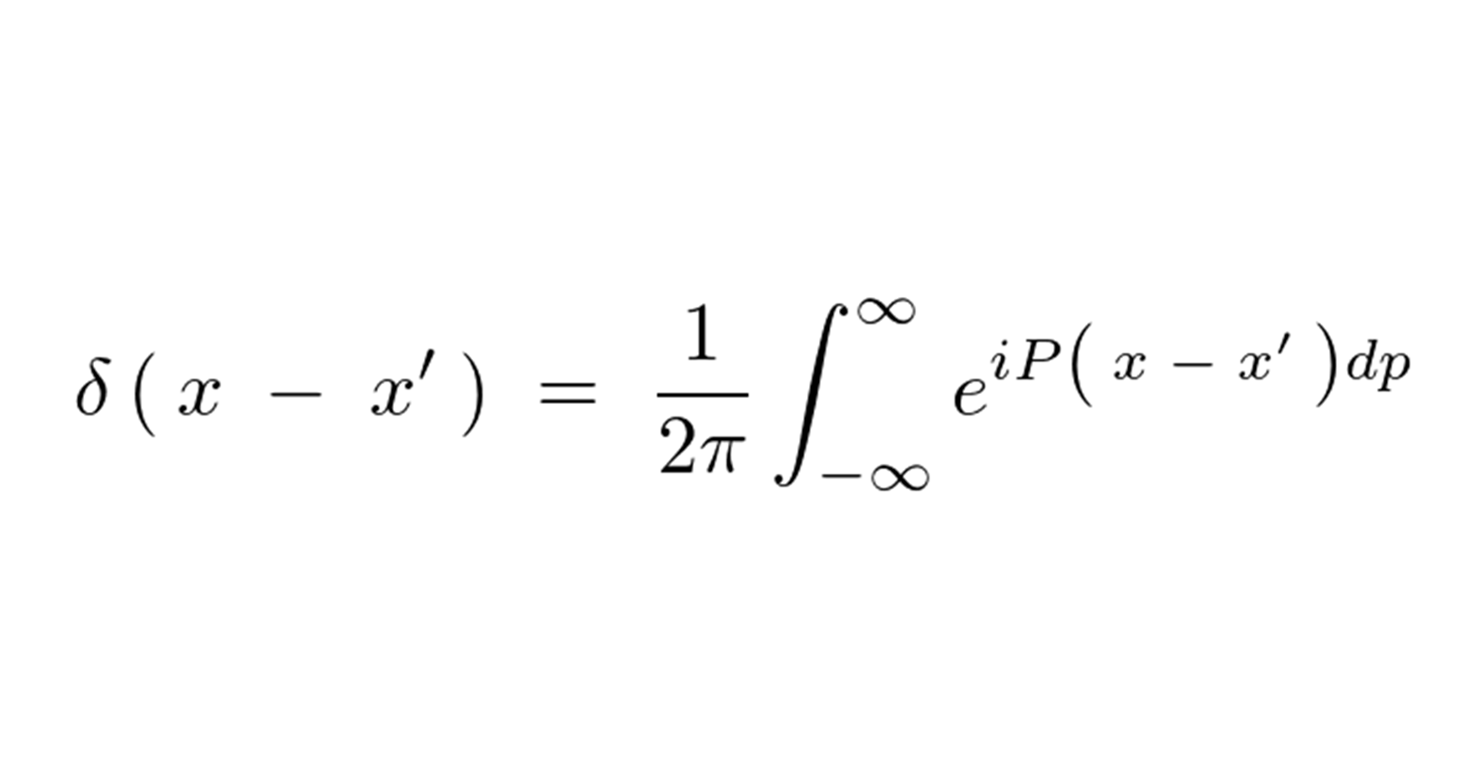
デルタ関数のフーリエ変換
続きを読む
-
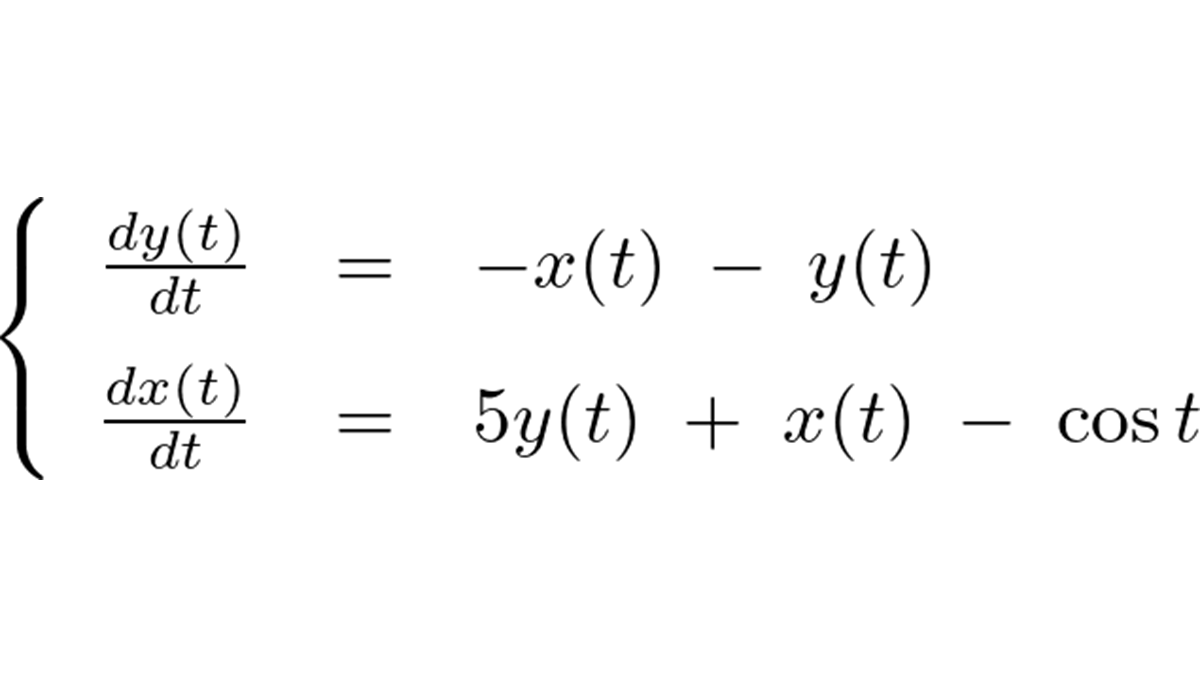
連立微分方程式の解法②
続きを読む
-
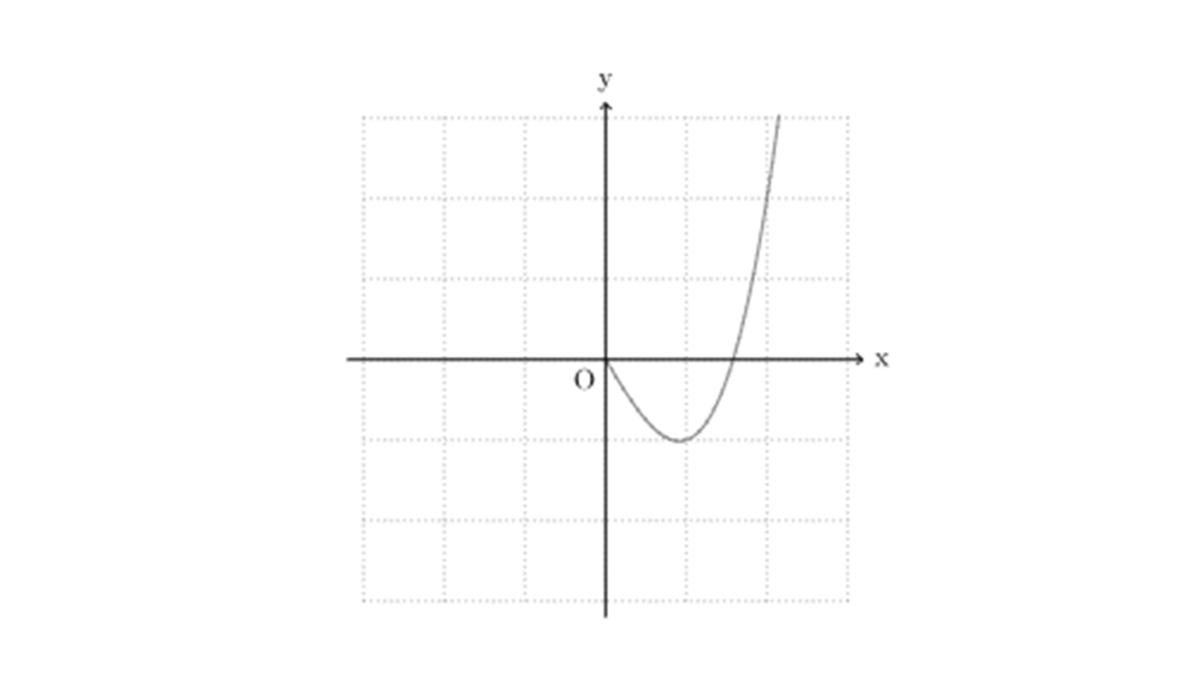
ヘヴィサイドの階段関数
続きを読む
-
コリオリ弾道軌道計算③
続きを読む