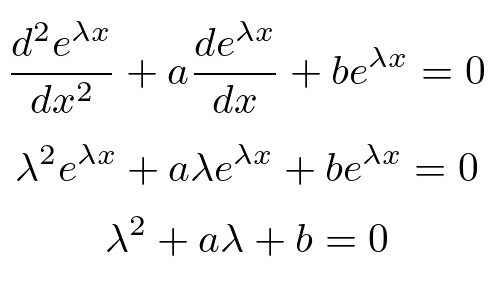1階常微分方程式
1階微分方程式
変数分離形
次の形の1階の微分方程式、
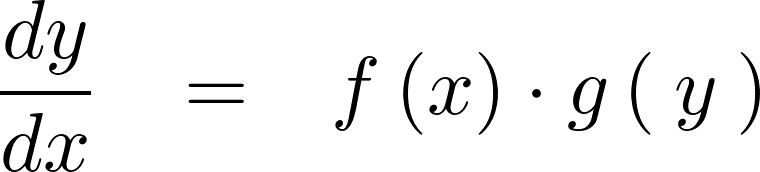
解き方としては、まず変数が2つあるので両辺にそれぞれを“分ける”ということをします。
上記式に関しては、左右の同じ変数を持つもの同士で分けるようにしてそれぞれを移動させると、
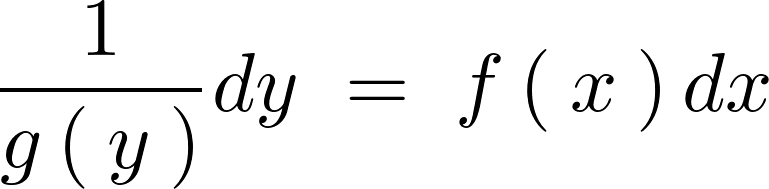
これを両辺にわたって積分します。
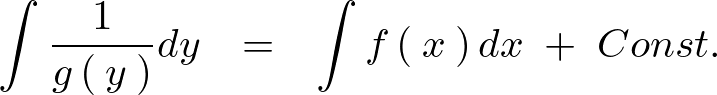
![]() というのは積分整数のことになります。特にことわりがなければ今後
というのは積分整数のことになります。特にことわりがなければ今後![]() と表します。
と表します。
例題1
以下のような微分方程式を考えます。
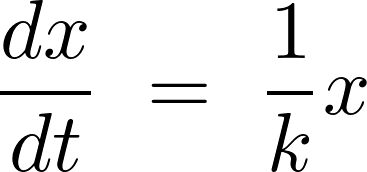
まず変数分離という作業をします。

それぞれを両辺にわたって積分していきます。
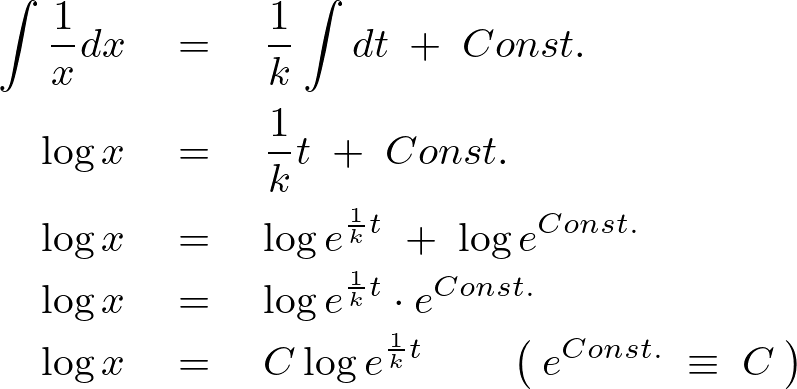
よって以下のように求まります。

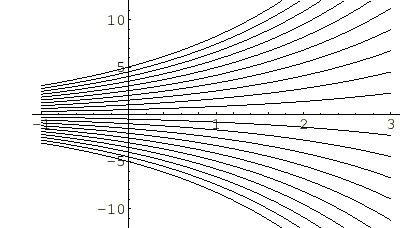
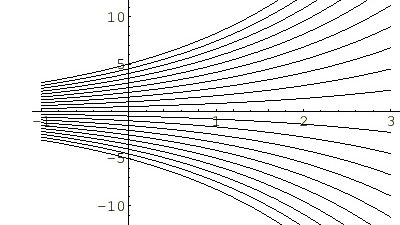
上図においては![]() の時の
の時の![]() をグラフ化したものになります。ラインは上記の積分計算によって出てきた積分定数の
をグラフ化したものになります。ラインは上記の積分計算によって出てきた積分定数の![]() の値を
の値を![]() から
から![]() の範囲で
の範囲で![]() 刻みでプロットしているためになります。
刻みでプロットしているためになります。
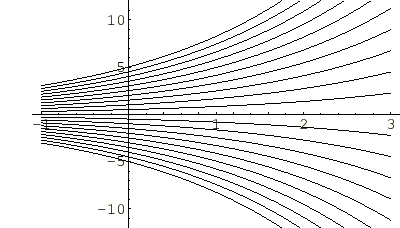
例題2
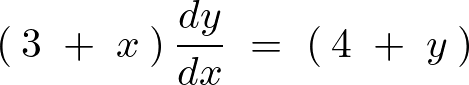
まずは変数分離を行います。
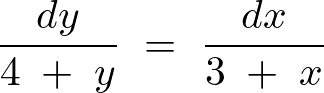
次に両辺を積分します。
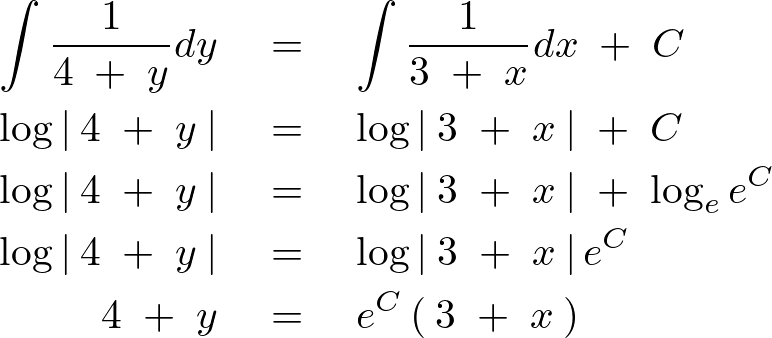
よって一般解は以下のようになります。
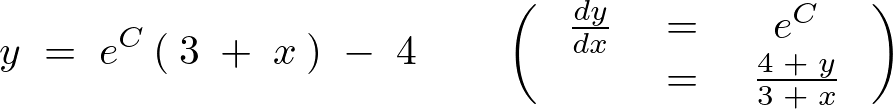
ロンスキアン
wait a moment!

Coming soon!
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.