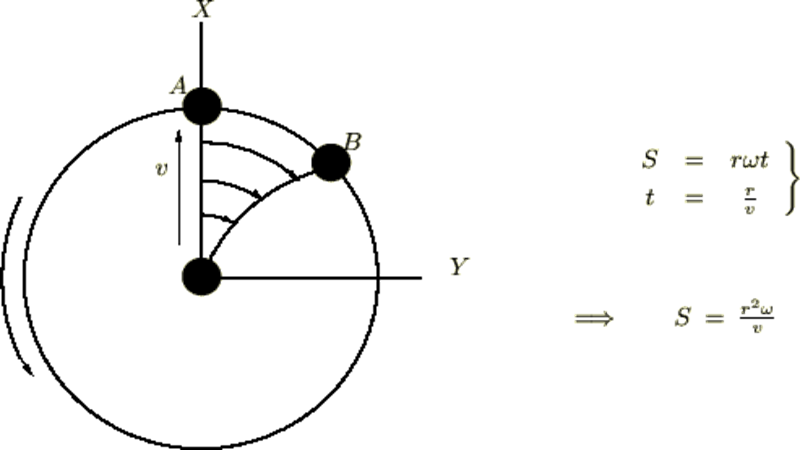
微分演算子による連立微分方程式の解法②
以下のような連立微分方程式を考えます。
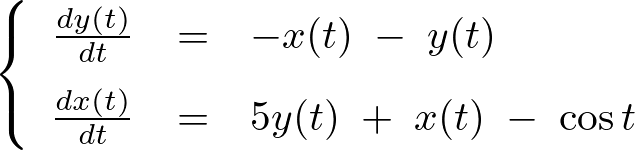
上記式の、
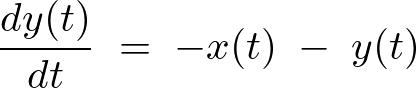
から計算していきます。
まずヘヴィサイド演算子法の表記を使って次のようにおきます。
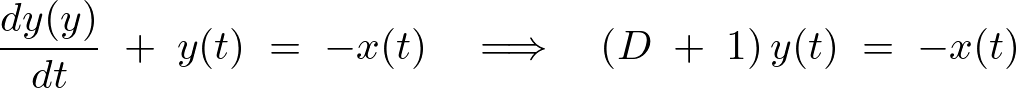
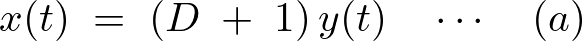
次に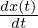 を変形させそれに
を変形させそれに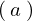 を代入します。
を代入します。

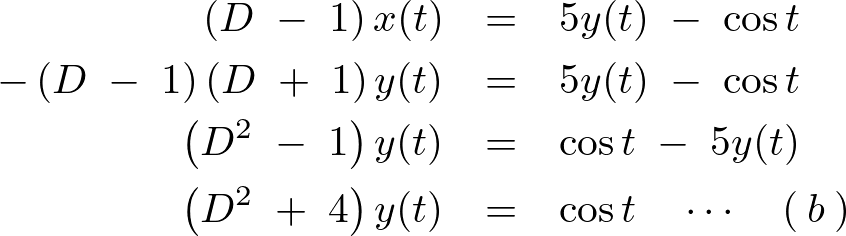
このときにおける同次方程式においての特性方程式は、
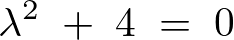
なので、
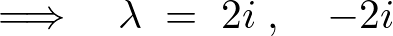
これにより一般解は、
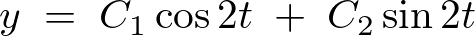
さらに特殊解においては の式を直接変形して、
の式を直接変形して、
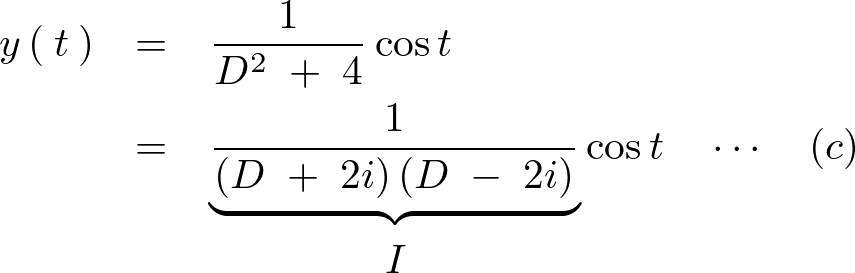
上記式の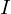 を少し変形させます。
を少し変形させます。
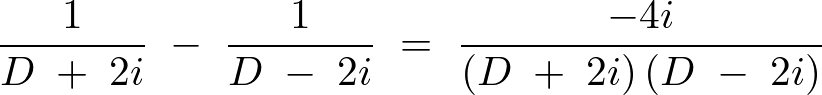
となるので上記 は、
は、
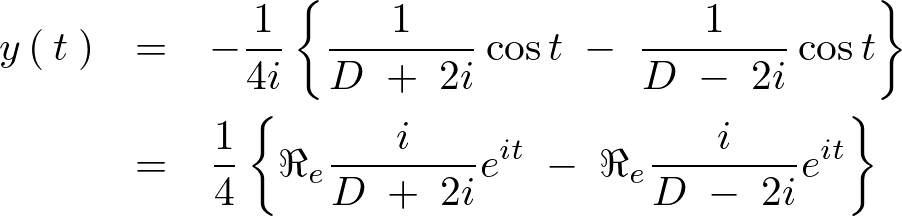
この式において求めるのはリアルナンバーになるので、
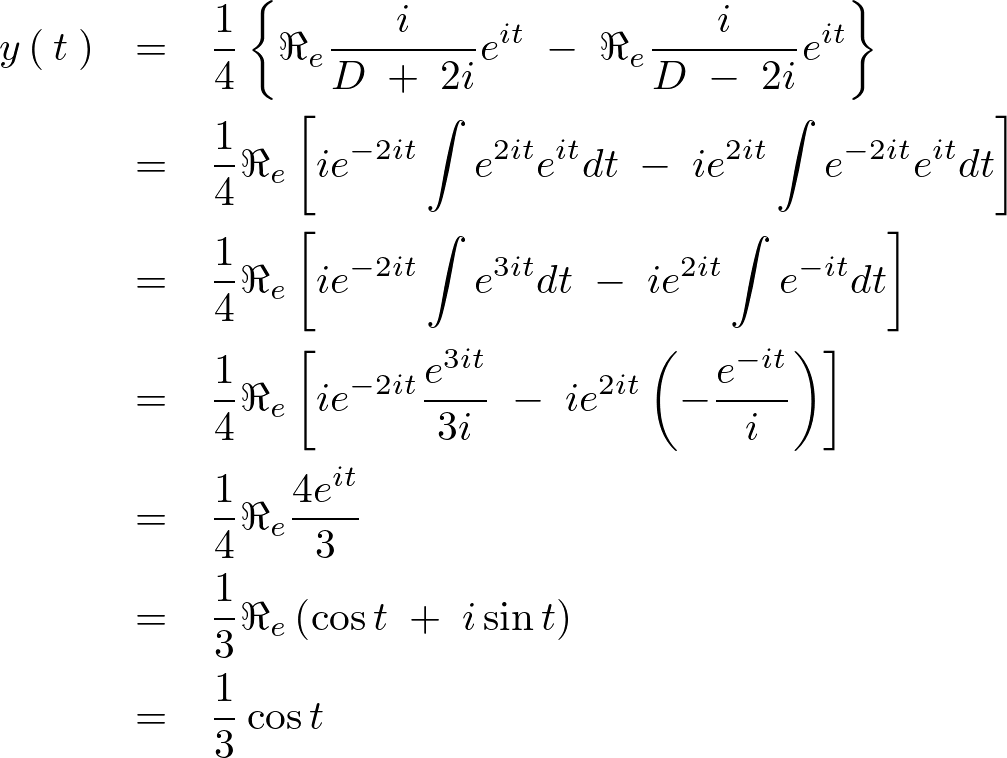
この結果によって、
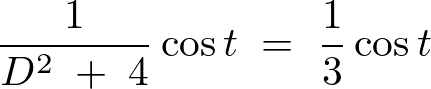
以上の結果をまとめればこの非同次方程式の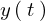 の一般解は次のようになります。
の一般解は次のようになります。
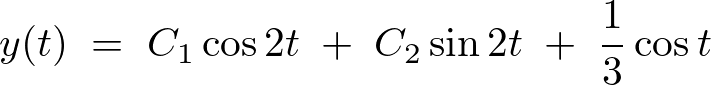
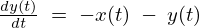 へ、
へ、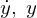 を代入します。
を代入します。
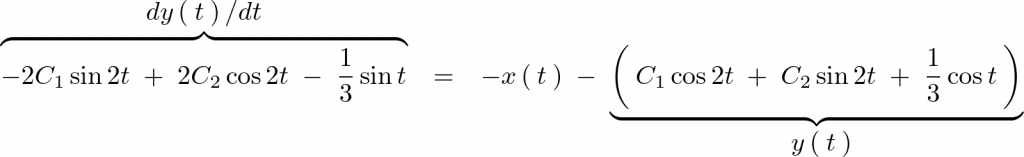
より、
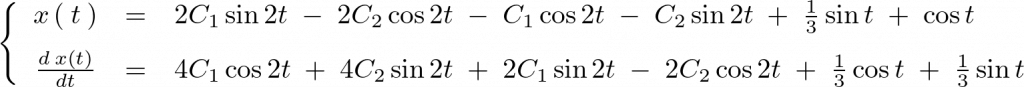

連立微分方程式の解法①
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

連立微分方程式の解法②
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
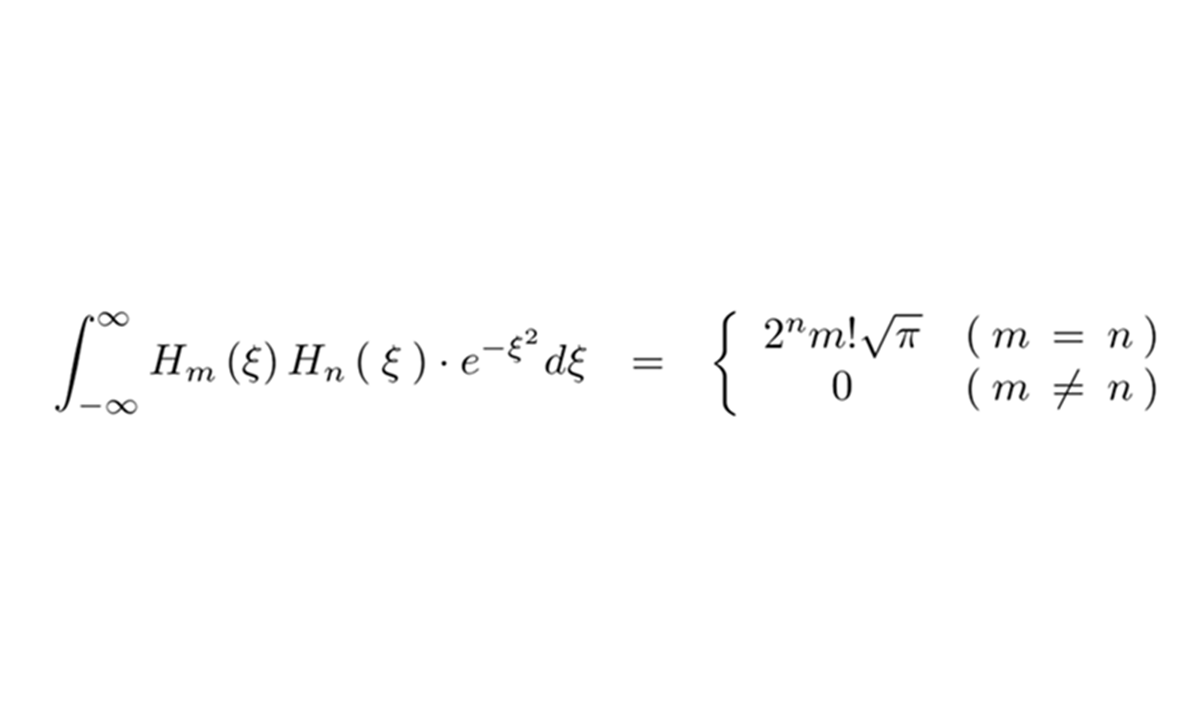
エルミート多項式の直交性
続きを読む
-
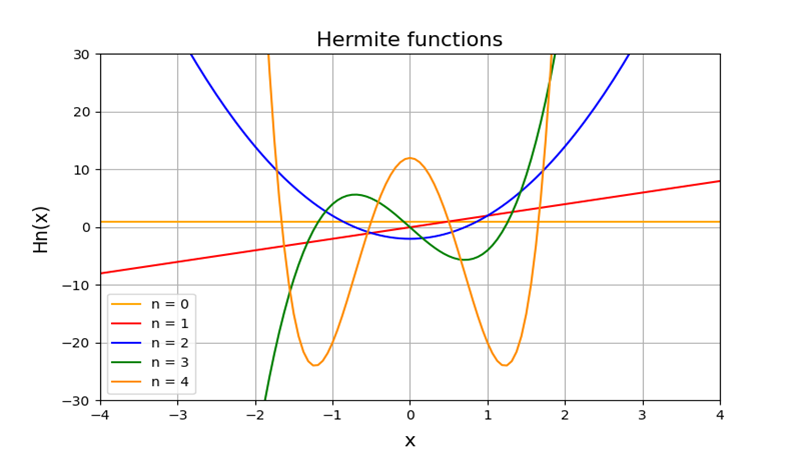
エルミート多項式の諸性質
続きを読む
-
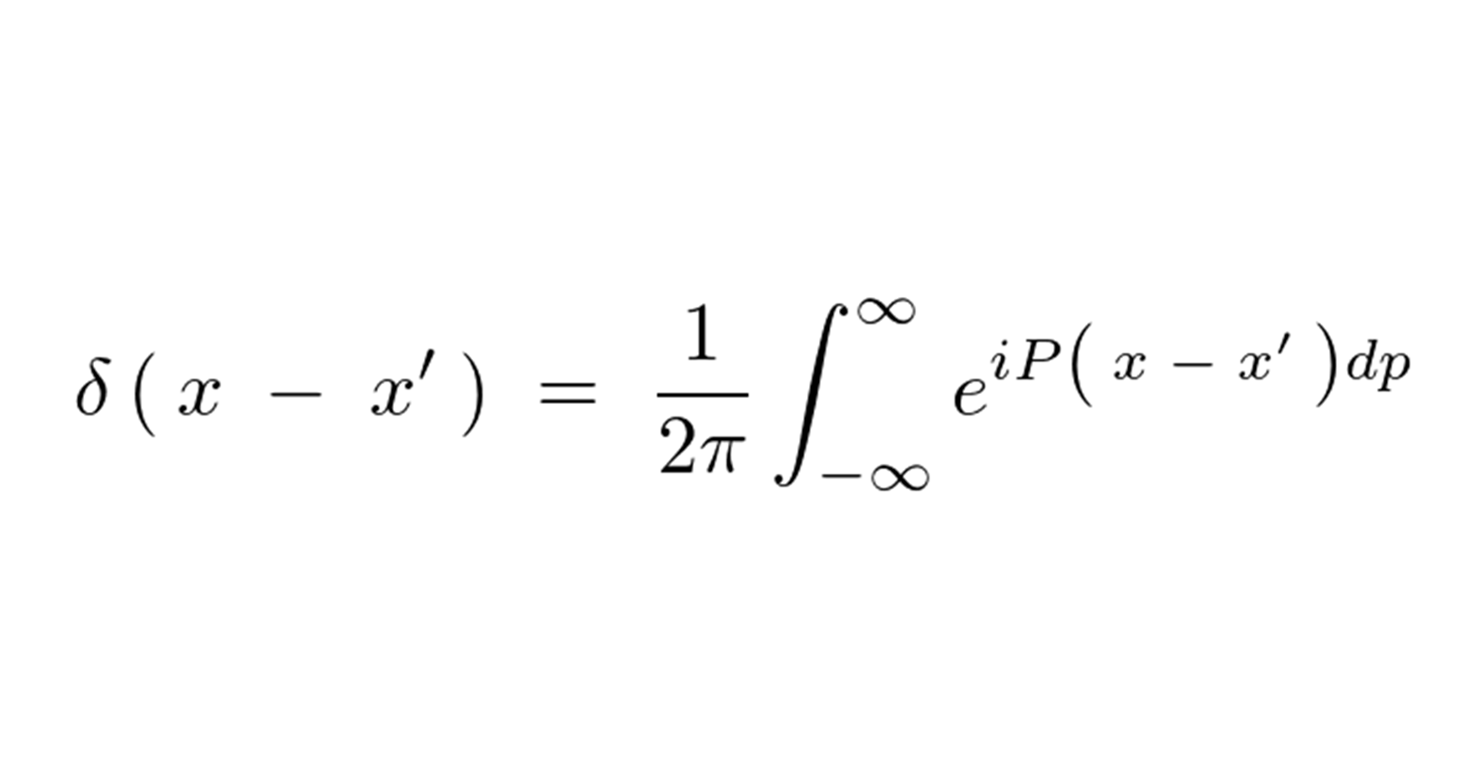
デルタ関数のフーリエ変換
続きを読む
-
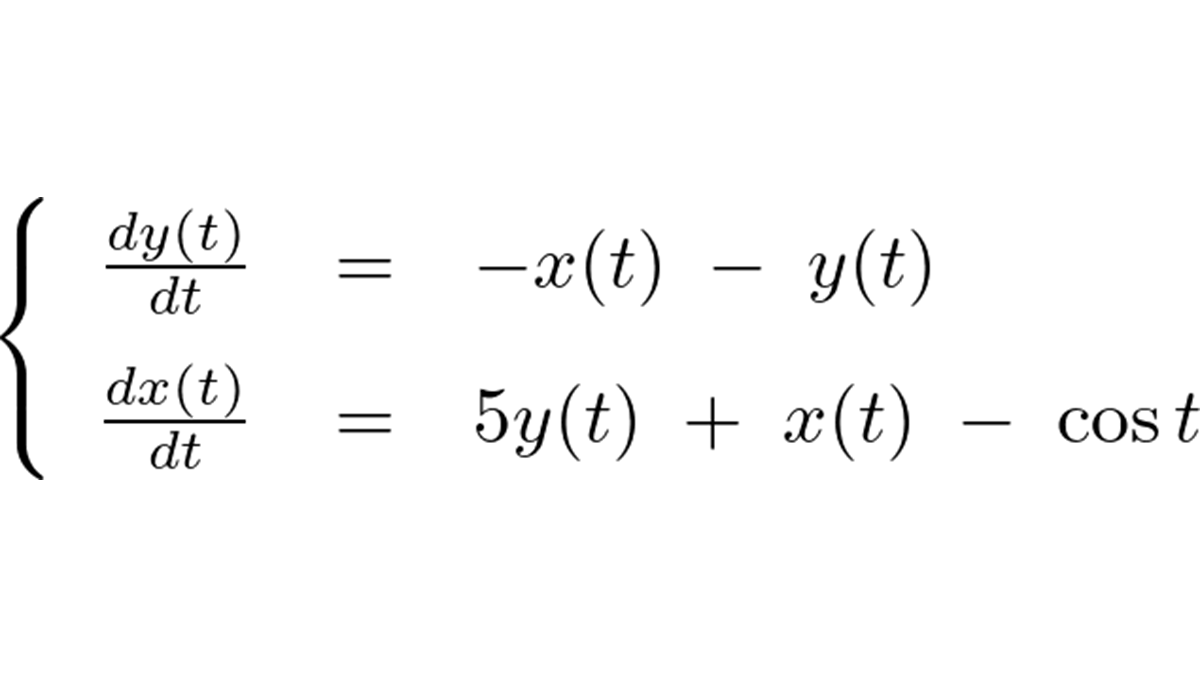
連立微分方程式の解法②
続きを読む
-
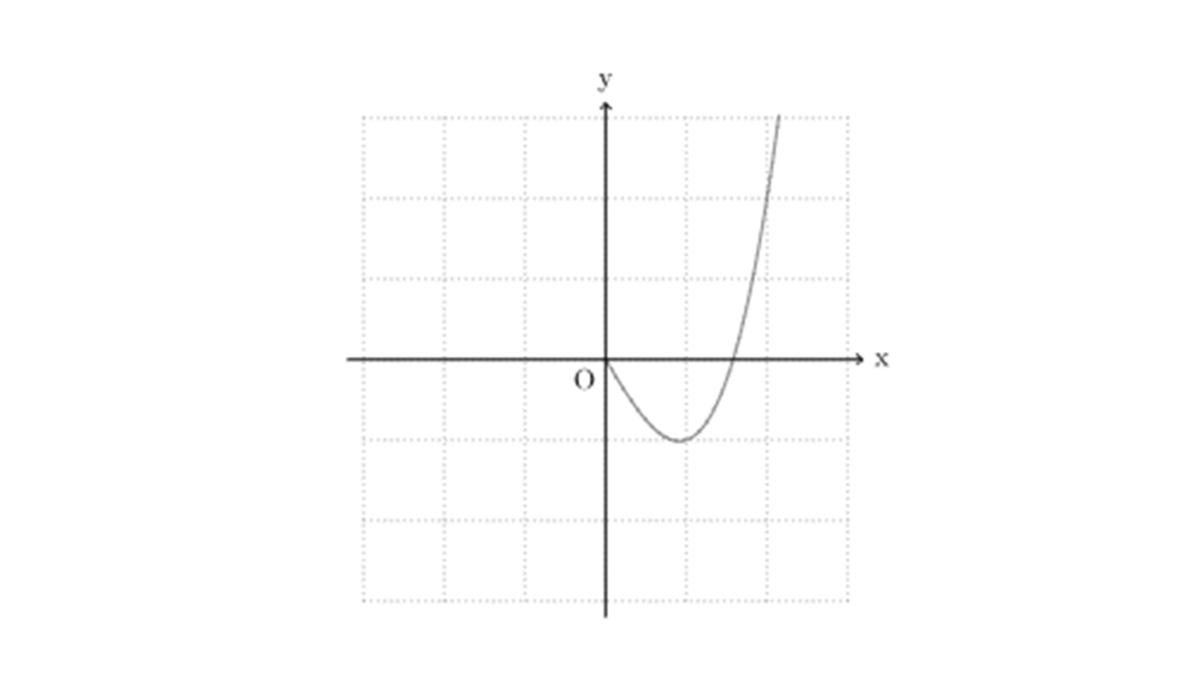
ヘヴィサイドの階段関数
続きを読む
-
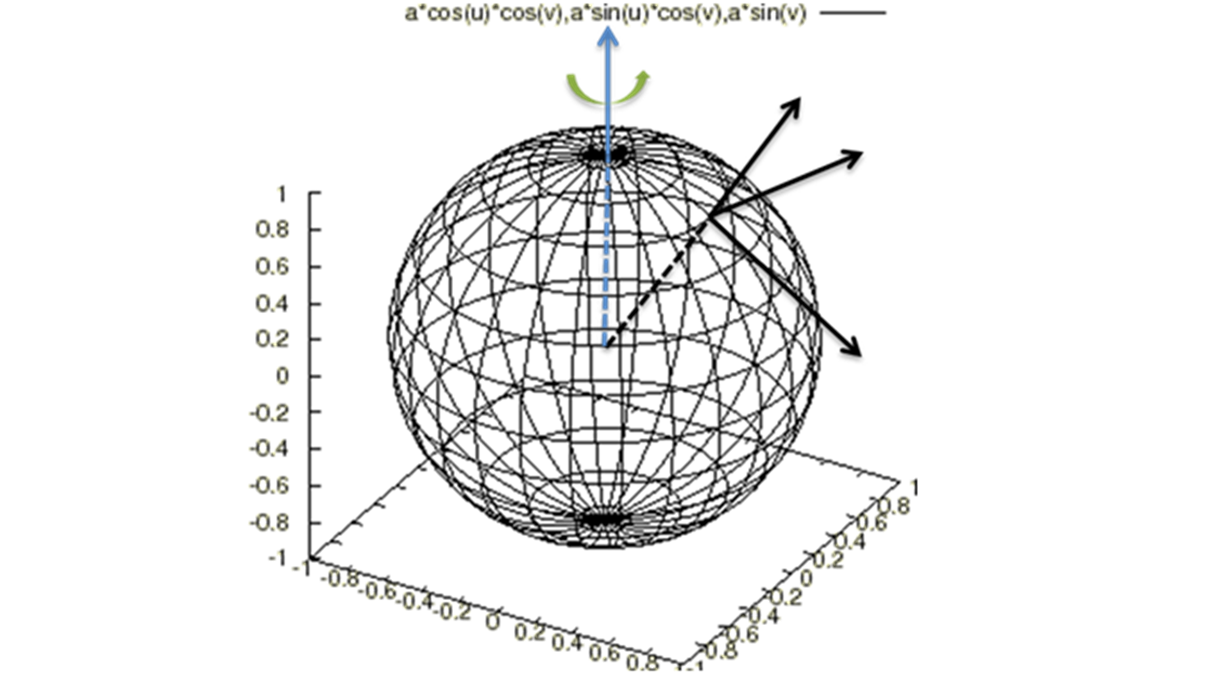
コリオリ弾道軌道計算③
続きを読む