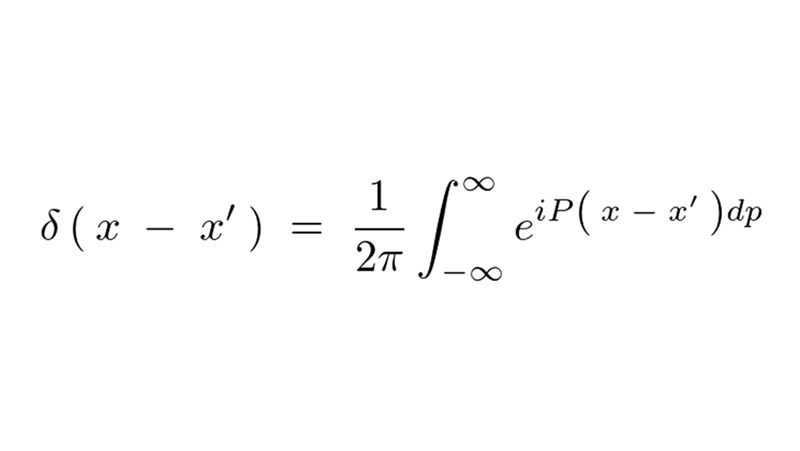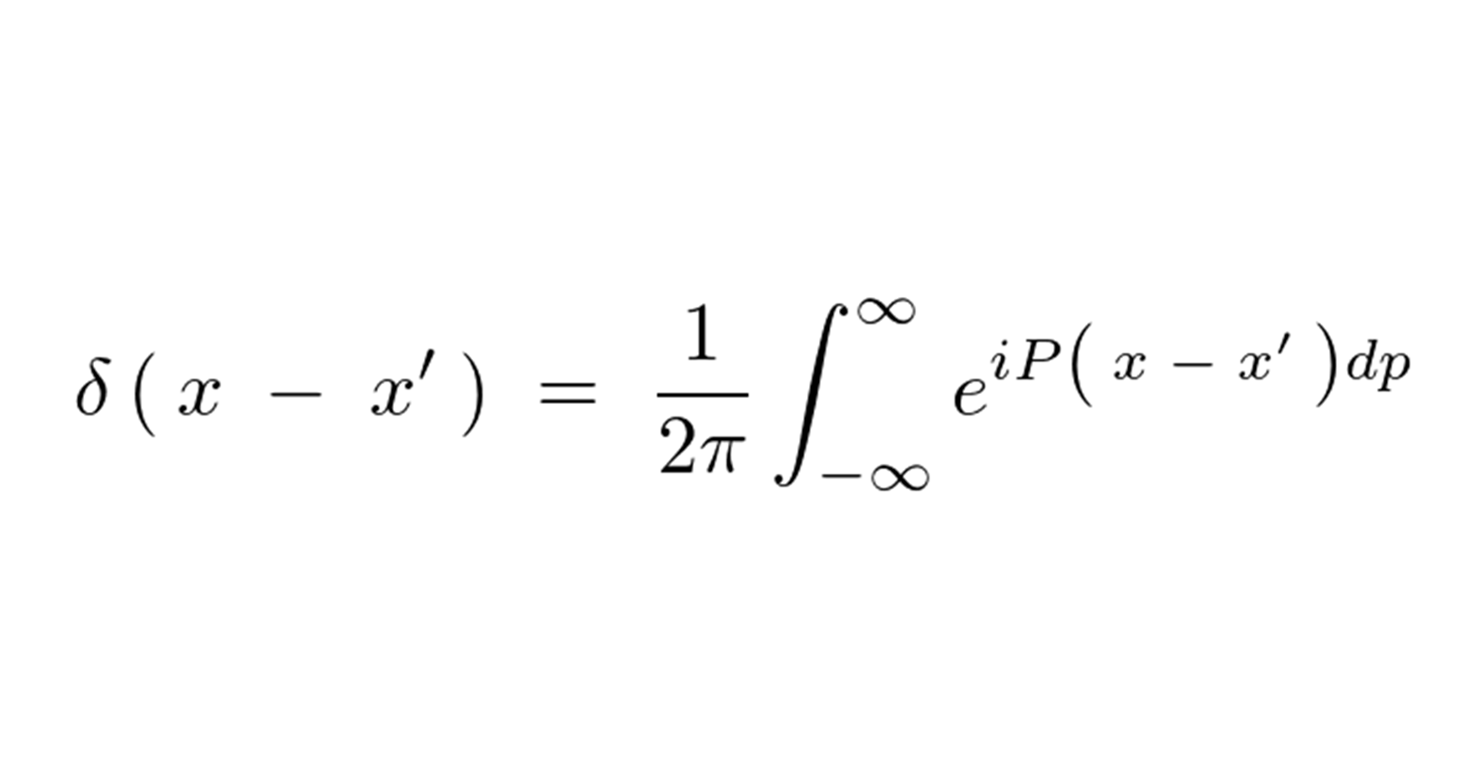フーリエ変換とは
フーリエ変換とは、関数を入力として受け取り、もとの関数に対して周波数がどのように存在するかを別の関数によって出力する積分変換法になります。
まずある関数 を考えます。ここで虚数単位を
を考えます。ここで虚数単位を![]() とすると、
とすると、 のフーリエ積分表示は、
のフーリエ積分表示は、
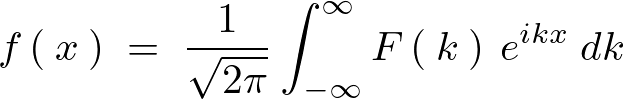
このときの上記式内の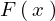 を
を のフーリエ変換といい、具体的には次のように書きます。
のフーリエ変換といい、具体的には次のように書きます。
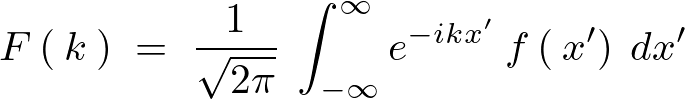
実際の現象を微分方程式などに置き換えた場合、その因果律を導き出すということは簡単なことではありません。
そこでこのフーリエ変換という技法を使うとその現象がわかりやすくなるという利点があります。
例えばつぎに示すような方程式があったとします。
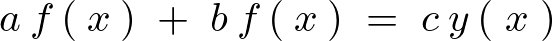
これに対して実際にフーリエ変換を施すと次のようになります。
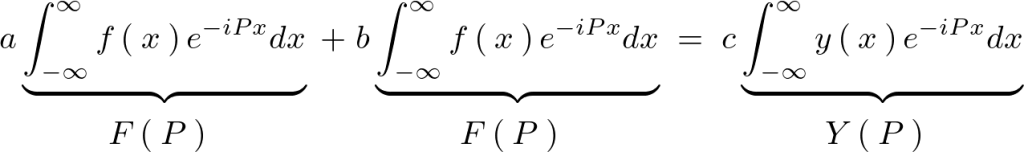
これより、
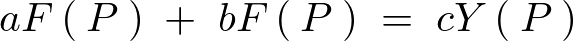
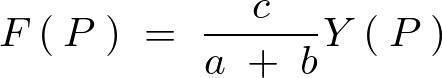
こうすることにより![]() の世界における現象が
の世界における現象が の世界の現象に置き換わっています。そうすると今まで
の世界の現象に置き換わっています。そうすると今まで![]() の世界で見ていた場合わかりずらかったものが
の世界で見ていた場合わかりずらかったものが に置き換わることで見通しが明るくなり、その現象がわかりやすくなるという利点があるからです。
に置き換わることで見通しが明るくなり、その現象がわかりやすくなるという利点があるからです。
普段私たちが生きている世界において、さまざまの現象や問題に対し研究や調査によりその理解を助けるためにはある視点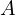 を別の視点
を別の視点 から(位相を変える)見通せば新たな視点が得られ理解が深まるということが経験上よくあることと思います。これは、Aという世界だけで見ていたものをBという世界で見た場合、以前はわかりにくかった現象が明確になり、理解しやすくなることを意味します。
から(位相を変える)見通せば新たな視点が得られ理解が深まるということが経験上よくあることと思います。これは、Aという世界だけで見ていたものをBという世界で見た場合、以前はわかりにくかった現象が明確になり、理解しやすくなることを意味します。
このような視点の切り替えは、問題解決や知識の獲得においてきわめて有効な手段であるといえ、さらには新たな洞察をもたらすことがあります。
具体的な例
ド・ブロイ波のフーリエ変換
以下のような波形の関数を考えます。
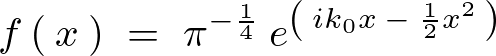
この式に対してフーリエ変換を施せば次のようになります。
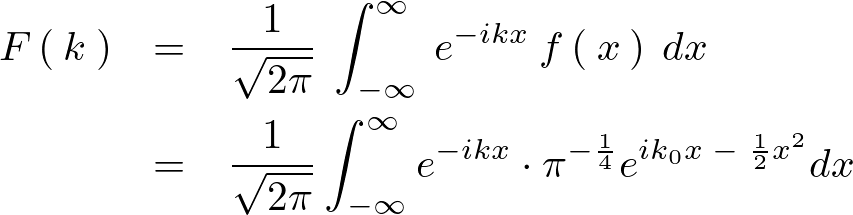
これを実際にフーリエ変換による計算をしていきます。
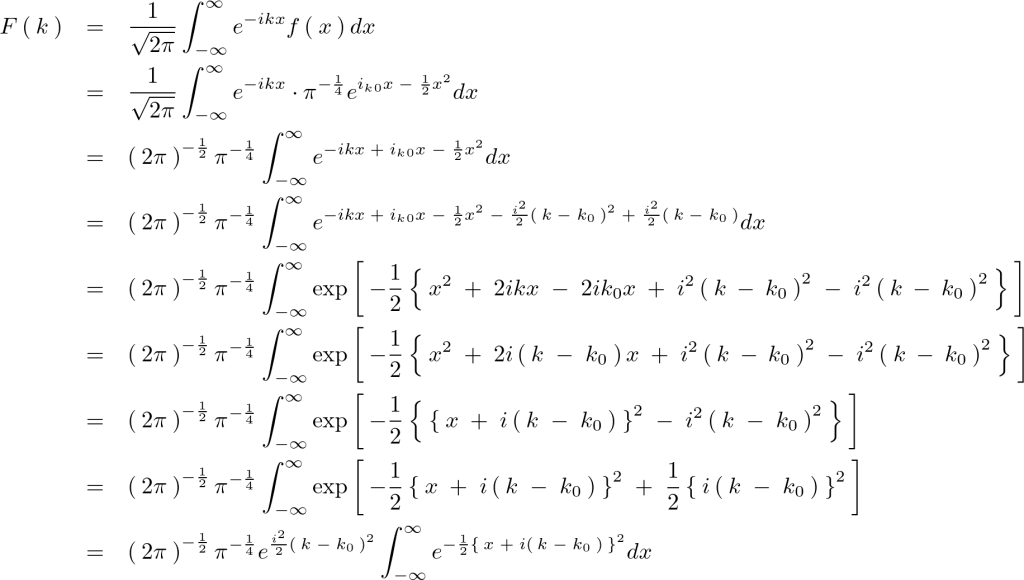
ここでいったん次のように置換して微分をして変数変換をします。
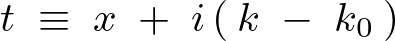
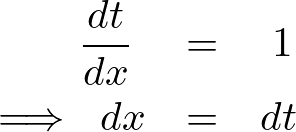
これを代入してさらに計算していきます。
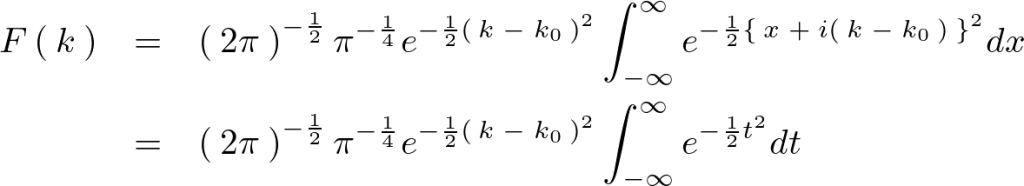
またさらに次のように![]() に関して
に関して![]() を使って変数変換をしていきます。
を使って変数変換をしていきます。
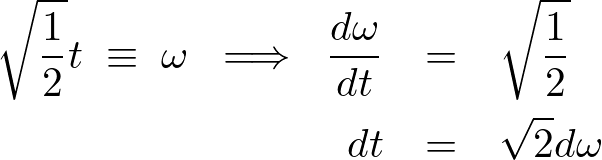
これを代入します。
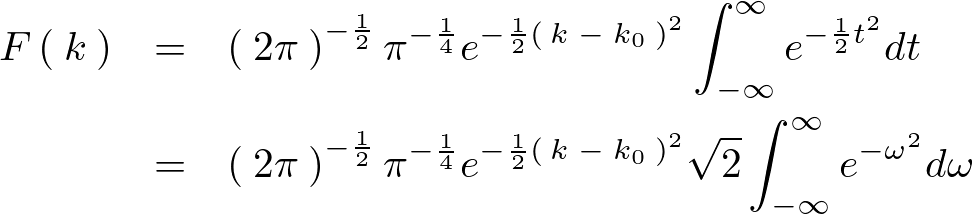
積分部分は上記のようにガウス積分になっています。
ガウス積分の公式は次のようなものでした。
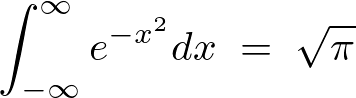
これを代入します。
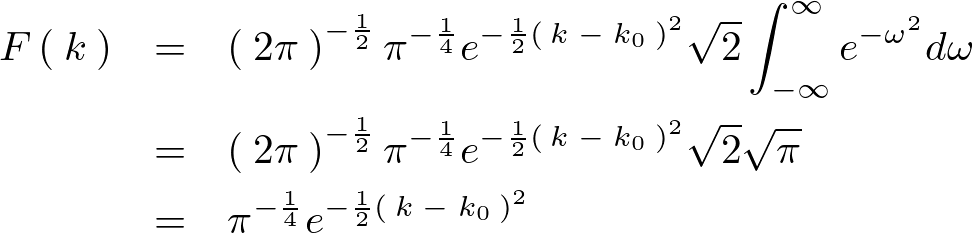
最終的に次のように求まります。
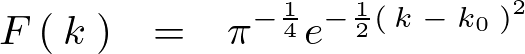
でてきた式を見ればわかるように先ほどの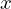 の世界のものが
の世界のものが だけの式に置き換わっています。こうすることにより今まではわかりずらかった現象がフーリエ変換を施すことによって見通しがよくなったりします。
だけの式に置き換わっています。こうすることにより今まではわかりずらかった現象がフーリエ変換を施すことによって見通しがよくなったりします。
このように、フーリエ変換さらにはラプラス変換といった数学分野はきわめて有用なツールになります。このカテゴリーではフーリエ変換に対して様々な視点から考察していきます。

ガウス関数の変換
準備中

Wait a moment
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Wait a moment
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.