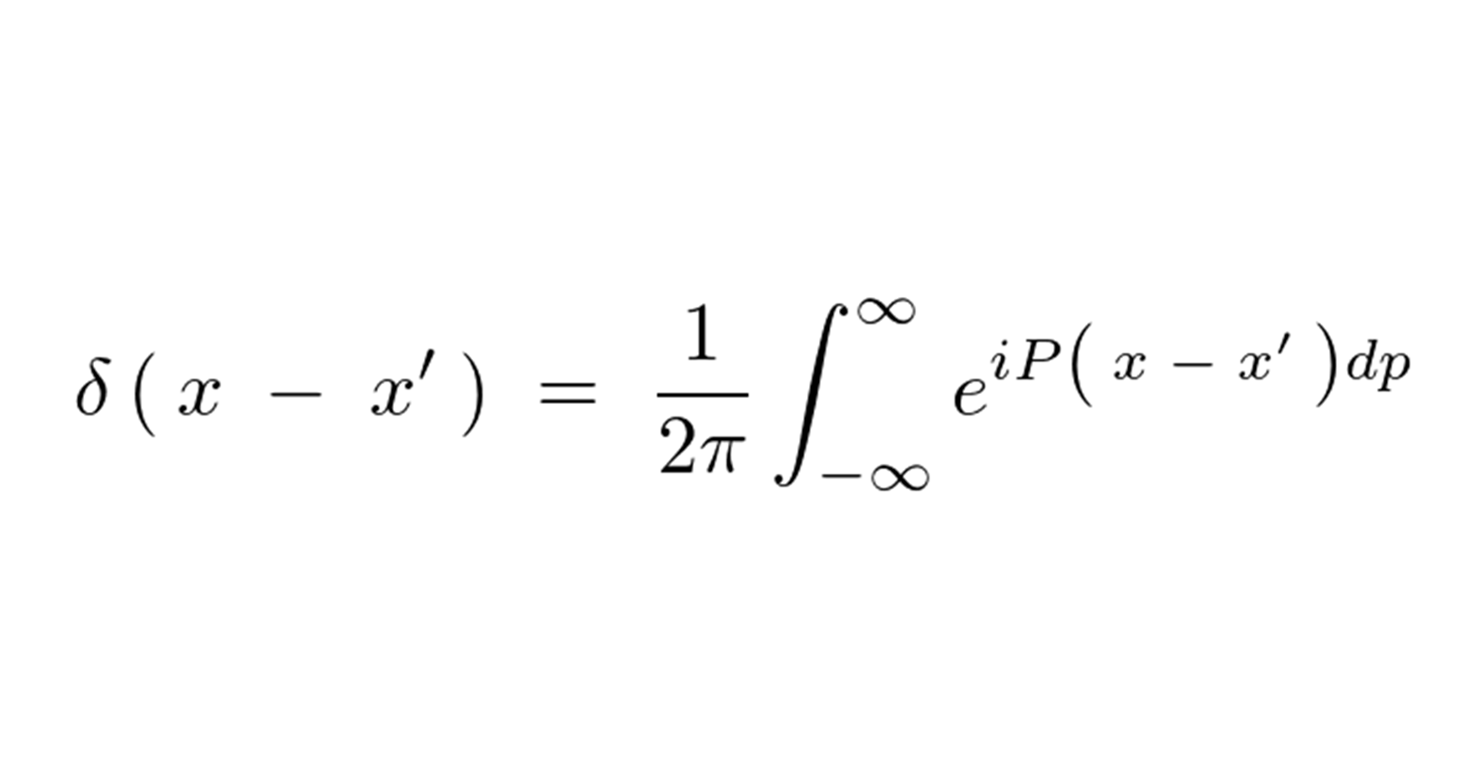デルタ関数のフーリエ変換
フーリエ変換の式
まずはある関数 を考え、ここで
を考え、ここで![]() を虚数単位とすると
を虚数単位とすると のフーリエ積分表示は、
のフーリエ積分表示は、
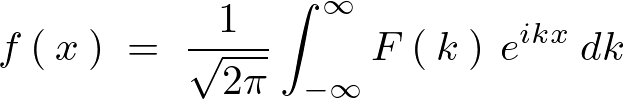
このときの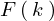 を
を のフーリエ変換といい、具体的には次のように書きます。
のフーリエ変換といい、具体的には次のように書きます。
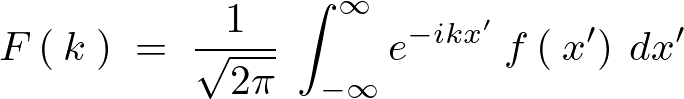
デルタ関数とは
ここでデルタ関数というものを導入し考察してみましょう。このデルタ関数というのは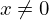 、つまり
、つまり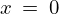 以外の場所においての値はすべて
以外の場所においての値はすべて で、
で、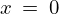 でのみその値が
でのみその値が![]() となり、かつその面積が“1”になると定義される関数です。
となり、かつその面積が“1”になると定義される関数です。
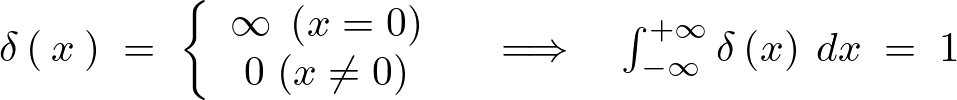
デルタ関数のその他の表し方:フーリエ積分表示
ある3次元空間(P空間)において次のように表現される関数、
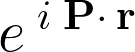
を考えこれに対して![]() (グラディエント)や
(グラディエント)や![]() (ダイバージェンス)などを作用させ変形していきます(これについての詳しい説明はベクトル解析を参照してください)。
(ダイバージェンス)などを作用させ変形していきます(これについての詳しい説明はベクトル解析を参照してください)。
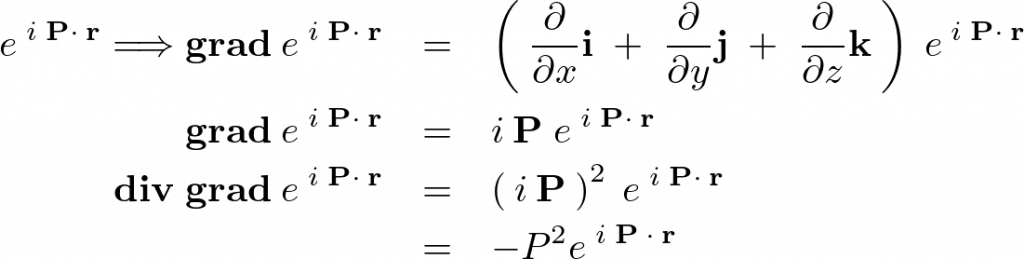
ラプラシアンを使って次のように表します。
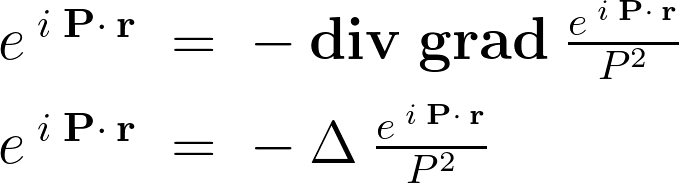
これの積分領域を全空間として表示すると次にようになります。
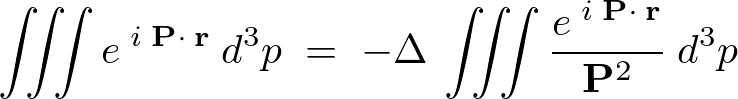
ここで![]() 空間の極座標に変換します。
空間の極座標に変換します。
ただし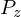 軸を
軸を![]() の方向になるようにとればその微小部分のヤコビアンは、
の方向になるようにとればその微小部分のヤコビアンは、
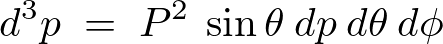
またドットプロダクトの基本定理により、
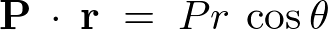
これらを利用して代入すれば次のようになります。
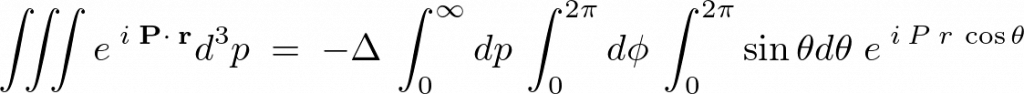
まず変数変換として![]() と置き、これを
と置き、これを![]() で微分すれば、
で微分すれば、
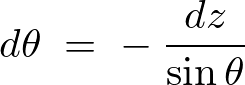
となるのでこれを代入します。
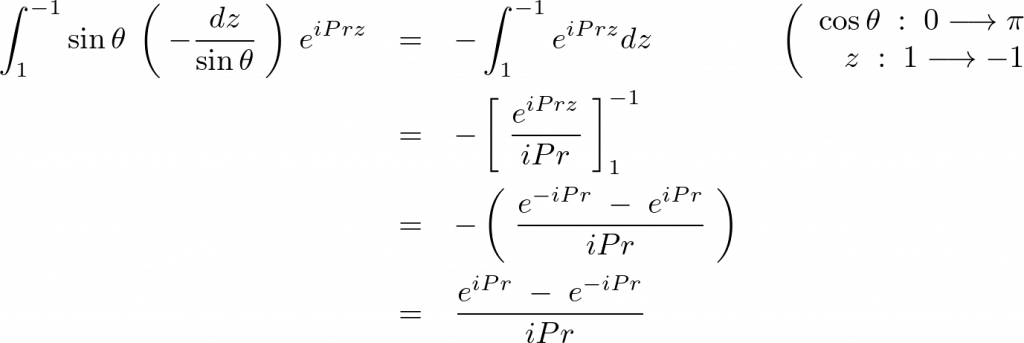
ここで三角関数の性質、
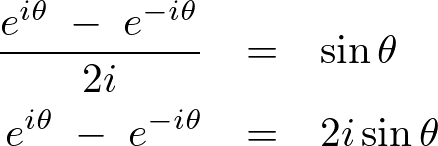
により、
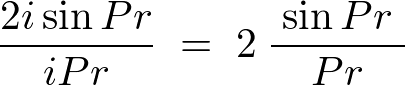
これを代入すれば、
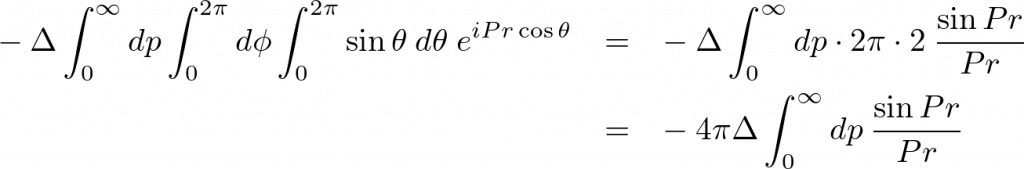
さらにここで次のような公式、
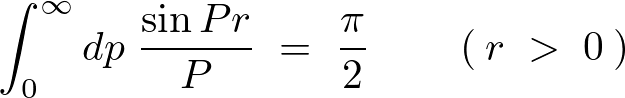
を使えば、
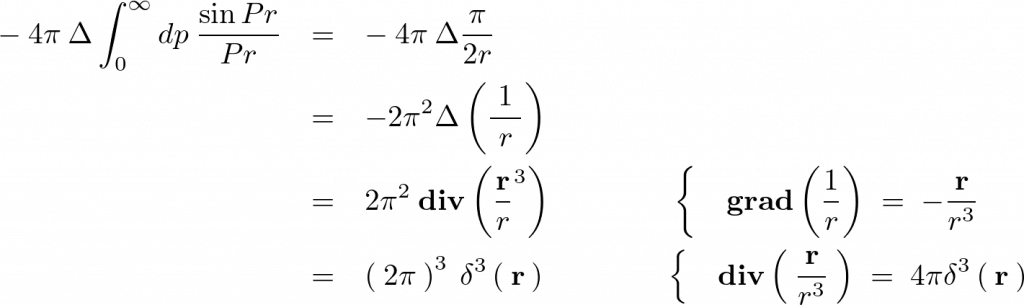
よって次のようになります。
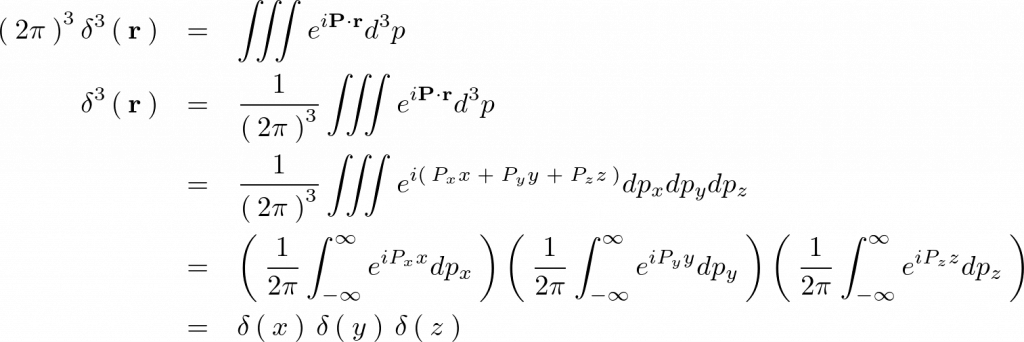
これにより一次元でのデルタ関数は次のようになります。
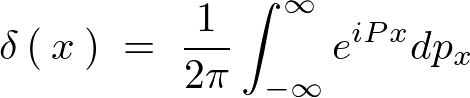
デルタ関数を使ったフーリエ変換式の求め方
今ここでこのデルタ関数![]() において$x$方向に
において$x$方向に![]() だけ水平移動させたとすればデルタ関数
だけ水平移動させたとすればデルタ関数![]() は,
は,
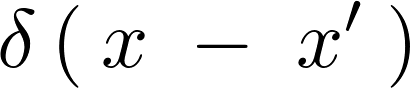
これを使えば先ほどの一次元デルタ関数は次のように表現できます。
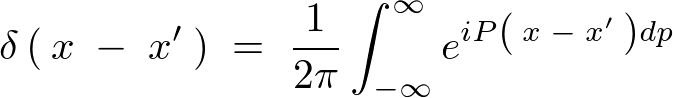
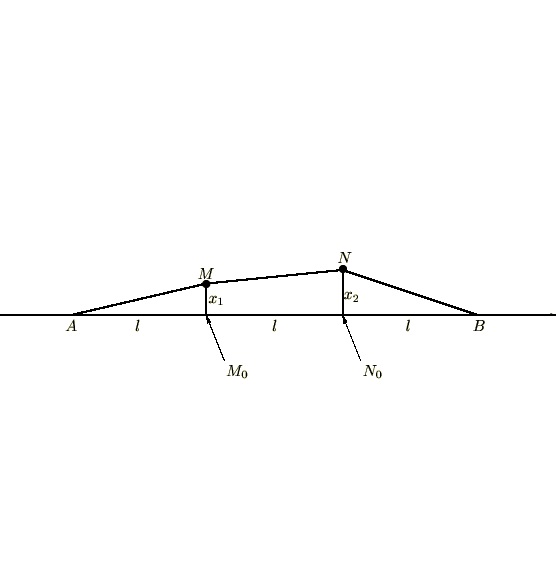
関数![]() において区間
において区間![]() との積は、
との積は、
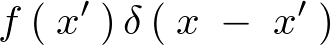
これを![]() から
から において積分を実行すれば、
において積分を実行すれば、
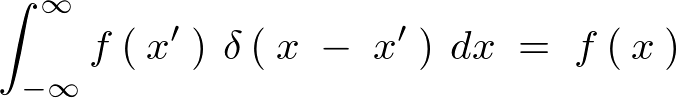
簡単にいうと非常に小さい区間においての長方形の面積を求めているといった感じで考えてください。
この式に![]() を代入します。
を代入します。
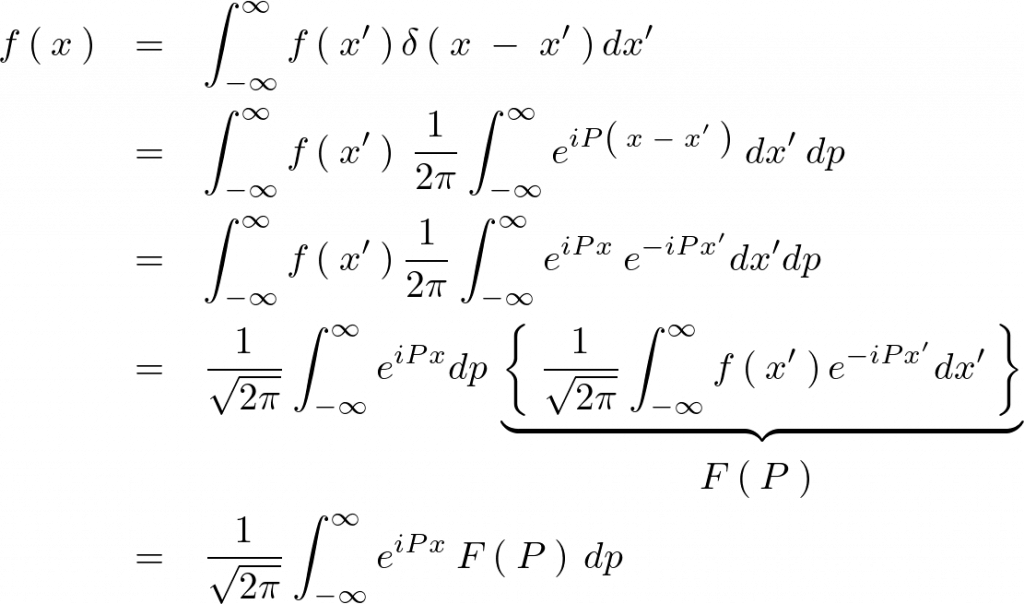
結果として次のように求まります。

出てきた式を見てわかるように上記式変形中において出てきた下部鍵括弧のなかのものは最初に示したフーリエ変換式です。そして右辺の一番最後に出てきた式をフーリエ逆変換の式といいます。
| フーリエ変換 | 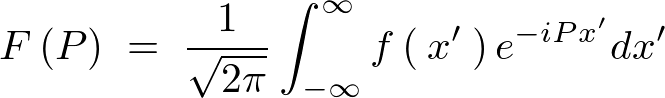 |
| フーリエ逆変換 | 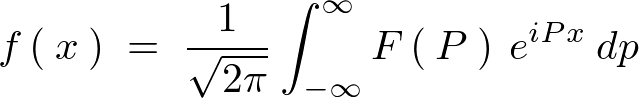 |

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
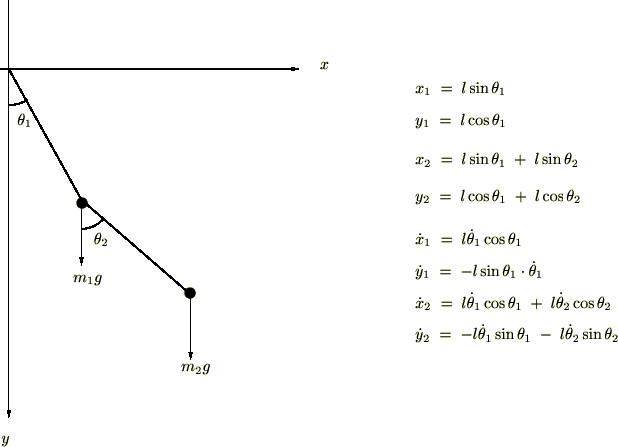
2重振り子②-微小でない場合
続きを読む
-
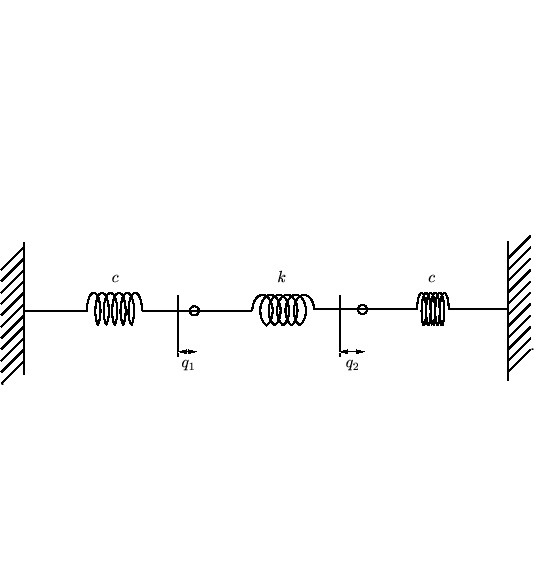
連成振動の解②━3重ばねの振動
続きを読む
-
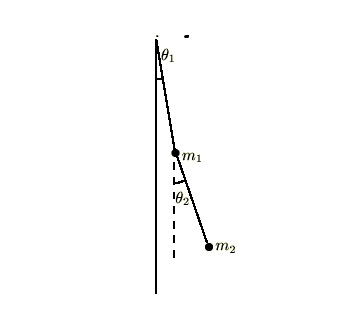
2重振り子①-微小な場合
続きを読む
-
連成振動の解①━弦の振動
続きを読む
-

ヘヴィサイド演算子法
続きを読む
-
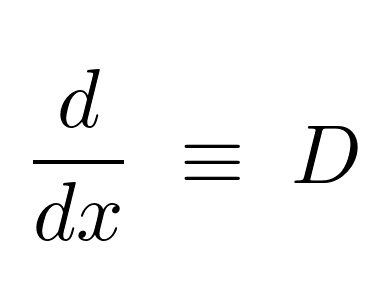
微分演算子による連立微分方程式の解法①
続きを読む
-
-
-
-
2024年6月8日マイグレーション完了
カテゴリー : 2024年6月8日マイグレーション完了diff-eq.comのドメインを取得してから約1年がたち、今年の3月末から本格運用を開始していたが、Cent…
-
-
-
-
-
-