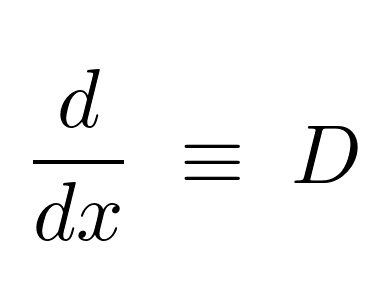コリオリ弾道軌道計算②
コリオリ長距離弾道軌道計算②
コリオリ弾道軌道計算①で求められた次の3つの連立微分方程式、
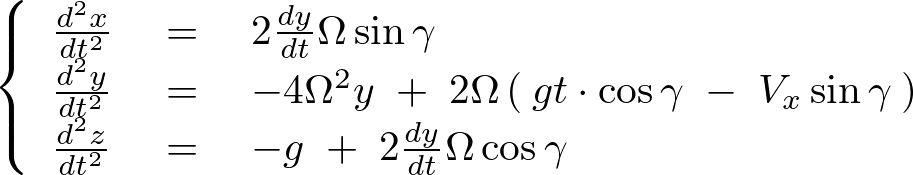
この連立微分方程式に関して具体的に解いていきます。
まず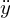 の式を計算していきます。
の式を計算していきます。
微分演算子法を使用した計算を行うために次のように置きます。
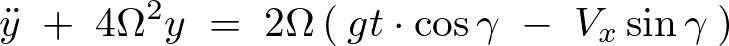
この微分方程式を解いていきます。
まず右辺の項が0とみなした解を求めるので上の式を次のように置きます。
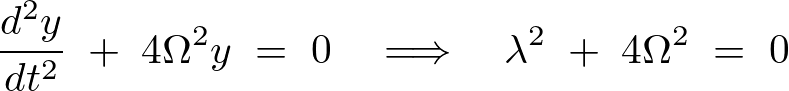
右の式を解いていきます。
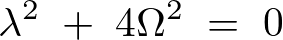
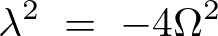
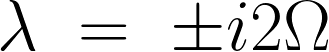
よって解は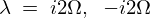 の二つになるので積分定数をそれぞれ
の二つになるので積分定数をそれぞれ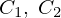 と置けば一般解は次のようになります。
と置けば一般解は次のようになります。
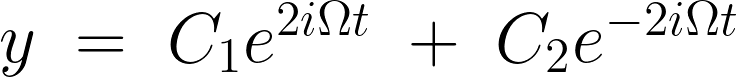
次に特殊解を求めます。
2階非同次微分方程式を解いていくことになりますが、ここでは微分演算子法(ヘヴィサイド法)により解を求めていきます。ロンスキアンによる解法はまた別のセクションで取り扱います。
微分演算子法により、
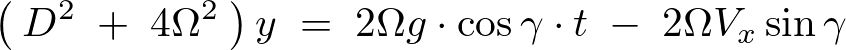
より、
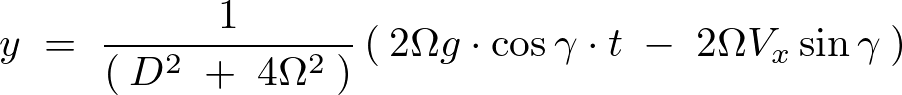
微分演算子法による特殊解の解法になりますがこのままだと計算ができないので右辺の分母の作用素を部分分数分解をおこなって計算できるように変形していきます。
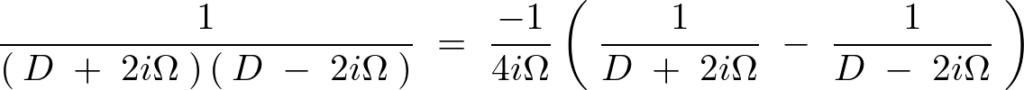
これより、
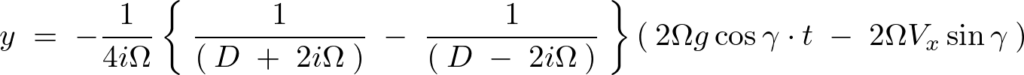
まず最初に、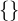 の中の作用素を二つに分けて計算していきます。
の中の作用素を二つに分けて計算していきます。
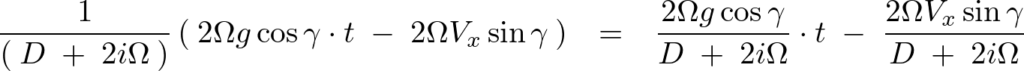
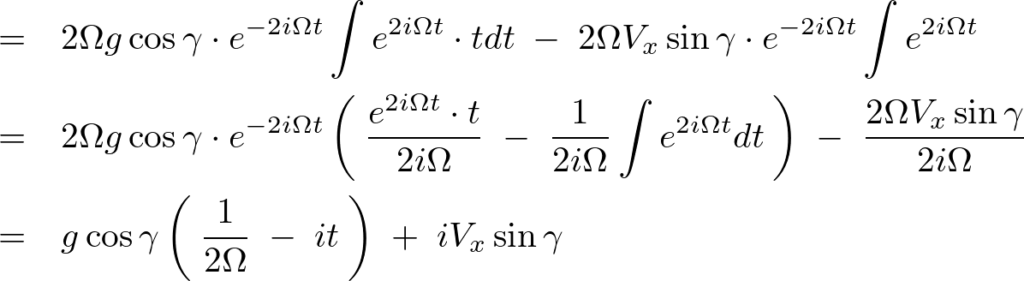
同様にして、
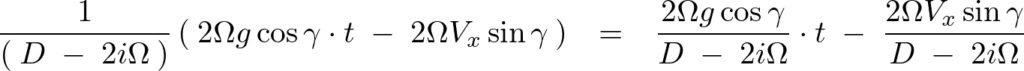
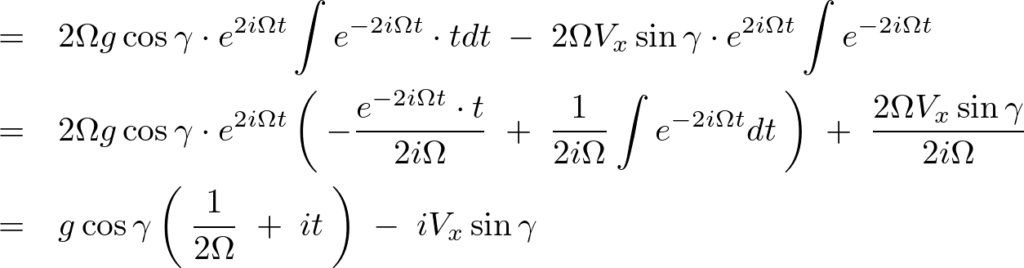
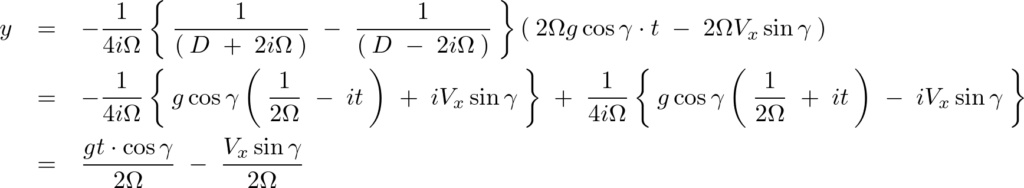
特解なので解をまとめると、
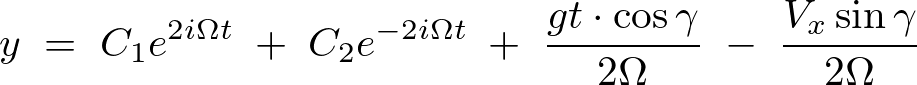
時間で一階微分します。
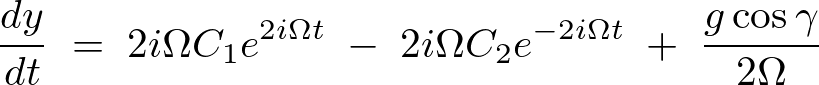
ひとまずのものをまとめると、以下のようになります。
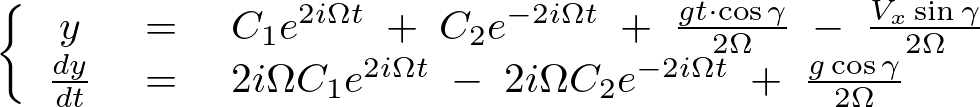
コリオリの力
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

コリオリ弾軌道計算①
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

コリオリ弾軌道計算②
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

コリオリ弾軌道計算③
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
1階常微分方程式
カテゴリー
-
フーリエ級数
カテゴリー
-
境界値に関する問題
カテゴリー
-
ラグランジュ関数
カテゴリー
-
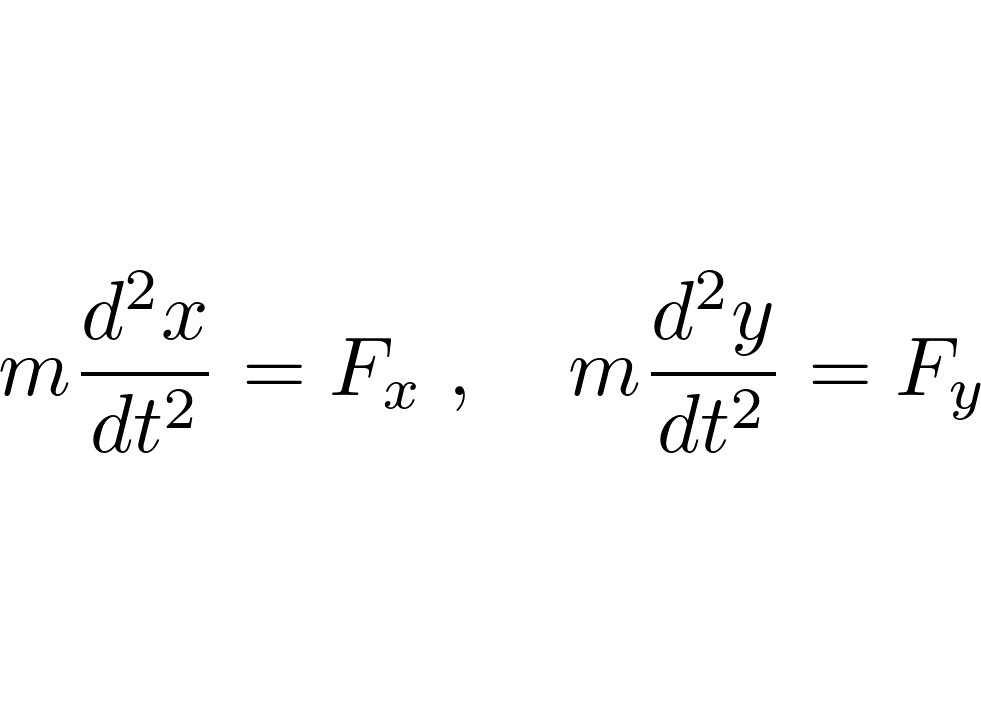
ラグランジュの運動方程式
カテゴリー
-

黒体放射とヴィーン変位則
カテゴリー
-
-
-
-
-
-
-
-
-
-
微分演算子による連立微分方程式の解法①
カテゴリー : 微分演算子による連立微分方程式の解法①オペレータ作用素をD=d/dtのようにおき、それを代数的に取り扱うことによって連立微分方程式の解をシステマティ…