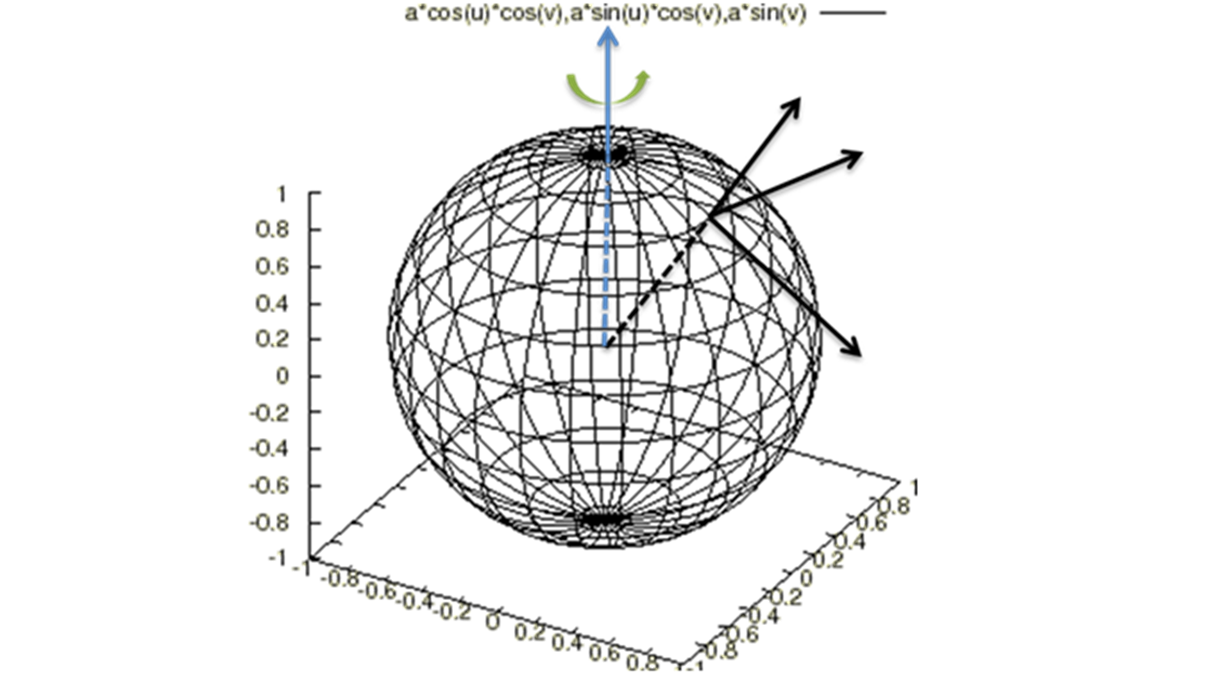
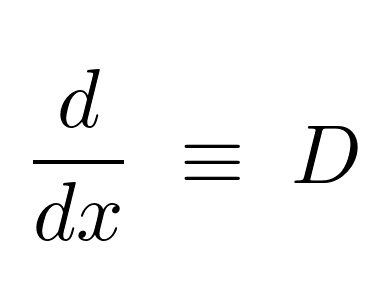コリオリ長距離弾道軌道計算③
コリオリ弾道軌道計算②のセクションにおいて、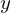 に関して求められた解をまとめると次のようになることがわかりました。
に関して求められた解をまとめると次のようになることがわかりました。
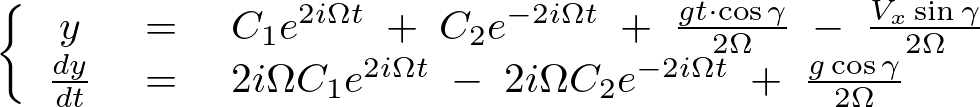
軽火器(アサルトライフル)による射撃を想定しているので![]() で
で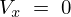 と考えられるので、
と考えられるので、
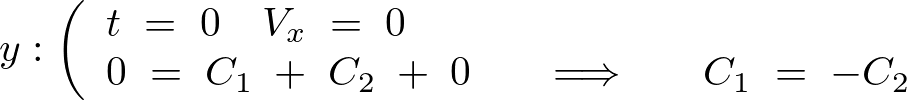
さらに速度の式に関しても同様に考えて、
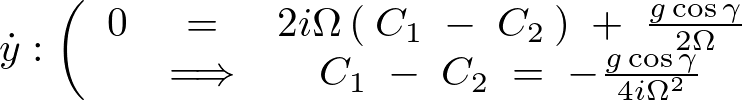
これらの結果により積分定数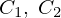 は次のようなものと考えることができます。
は次のようなものと考えることができます。
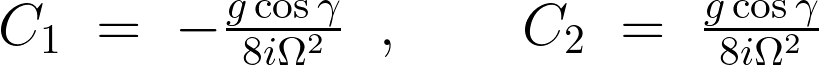
代入しまとめます。
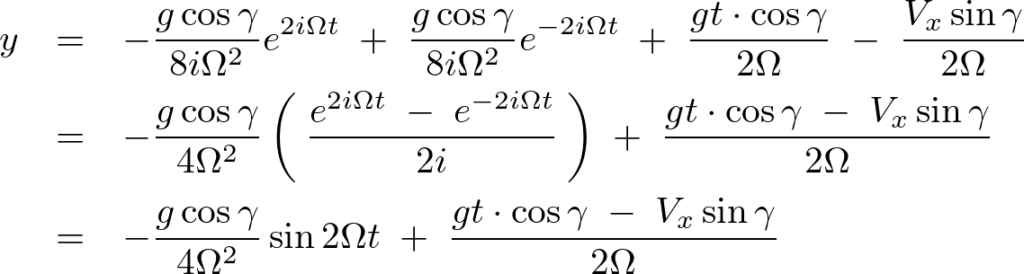
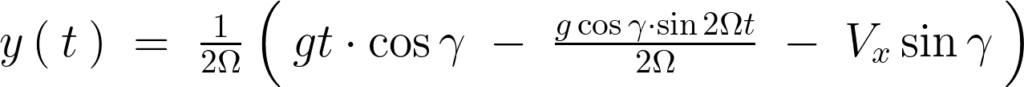
上記式を時間![]() で微分します。
で微分します。
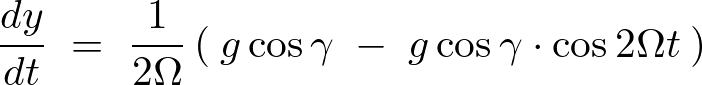
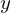 の解を
の解を![]() の式に代入します。
の式に代入します。
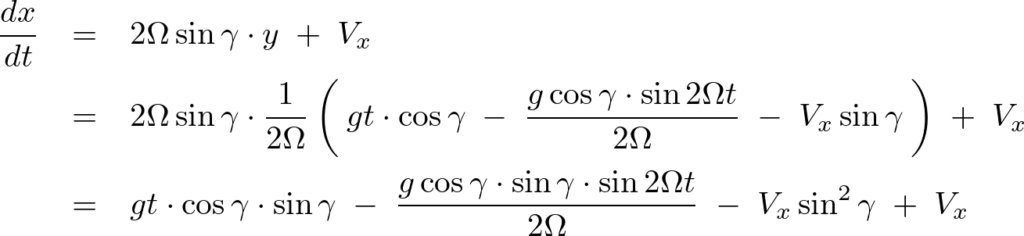
今度はこの式を積分します。
時間 から時間
から時間 までの飛行時間の発射を仮定しているので、
までの飛行時間の発射を仮定しているので、 の定積分を行います。
の定積分を行います。
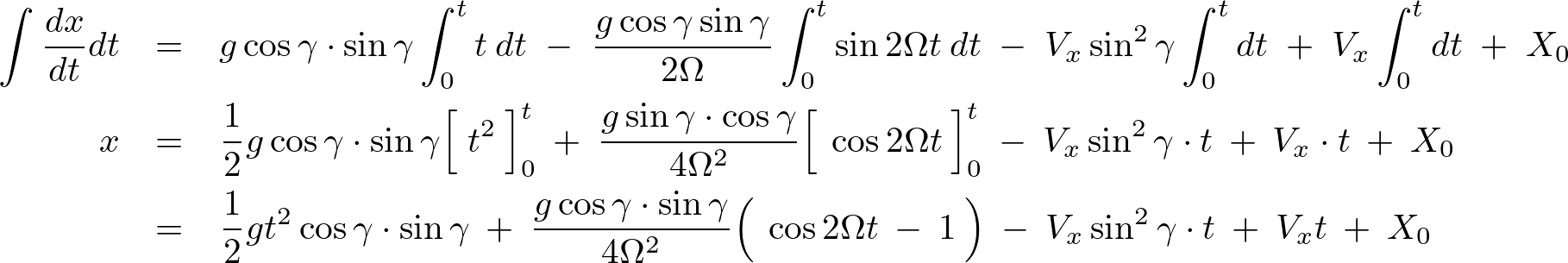
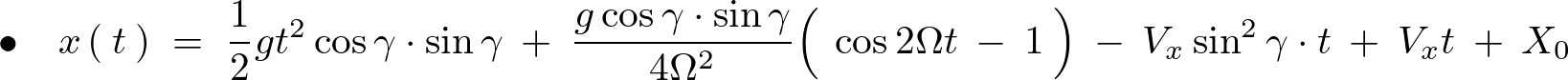
次に![]() の式に関して、
の式に関して、
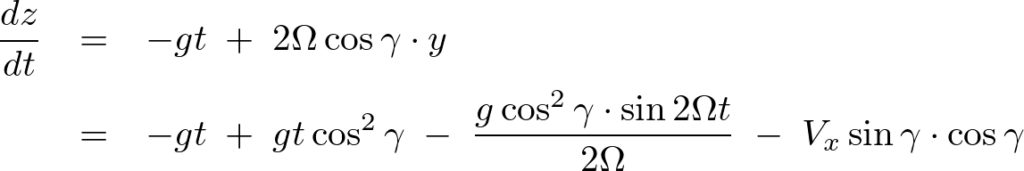
積分していきます。
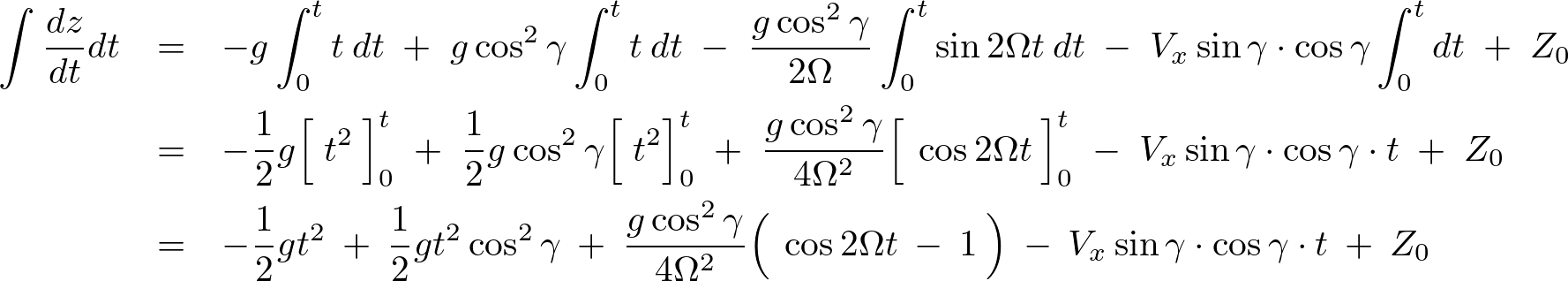
ここででてきた積分定数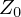 は高さ
は高さ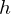 と置きます。
と置きます。
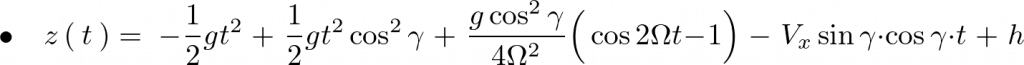
まとめると次のようになります。
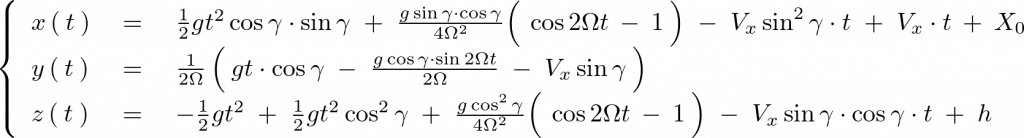
この結果はあくまで簡略化した運動方程式を計算していったものなので厳密に行う場合の弾道軌道計算解とは違うですし、連立微分方程式の因果律はあっていますが最初の方程式の組み立て方にも少なからず間違いがある可能性もあると思いますので、その辺のところは大目に見てください。
通常の射撃と長距離狙撃の違い
普通の感覚の人だと狙撃というのは、スコープにうつる標的に照準を合わせて、そしてその目標めがけて撃つようなイメージがありますが、実際には銃の性能や風向風圧重力などによる影響、さらには射撃範囲が数キロに及ぶ場合には上に計算したような地球の自転による見かけの力、“コリオリの力”を考慮しなければなりません。
一般的な人の場合は、たとえば左のイメージのようにスコープを覗いたとき標的となり得るべくターゲットの中心線の部分にきちんと狙いを定めて撃つものだと考えている人が大部分だと思いますが、実際には弾丸の動きを的確に考慮(予想)して照準の位置をずらして射撃するような格好になります。
つまり長距離狙撃においては弾丸を“標的に照準を合わせて撃つ”、のではなく、弾丸を“目標とする標的に持っていかせる”、といった感覚で行うものだと言ったほうがより正しい言い方になるかもしれません。
例えば狙撃ポイントが新宿の新大久保か、または大阪の生野区のような北半球の極でもなく赤道付近でもない中緯度付近(角度γ)における射撃、しかもその射撃距離が数キロにわたる場合においては、かなり大雑把な言い方にはなりますが上の左の絵(AA)ような標的に照準を合わせるのではなく、右の絵のように標的から左上あたりのポイントをねらって撃つことになります。
また、上の3式を見てもわかるようにすべての式に細かく緯度(角度γ)が与えられ、それぞれの式にはいくつもの要素、つまり風向風圧など気象条件なども絡み合っており、そのため弾丸を射出する緯度や方向によっても様々な結果が導かれることになります。結果的に「コリオリ弾道軌道を熟知した手練れ~」であったとしても、数キロ先に離れた標的を射抜くことはほぼ不可能であり仮にヒットしたとしてもそれは数うちゃ当たるうちの一つでしかないといえるものになると思います。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
-
-
-
-
-
-
-
-
-
微分演算子による連立微分方程式の解法①
カテゴリー : 微分演算子による連立微分方程式の解法①オペレータ作用素をD=d/dtのようにおき、それを代数的に取り扱うことによって連立微分方程式の解をシステマティ…