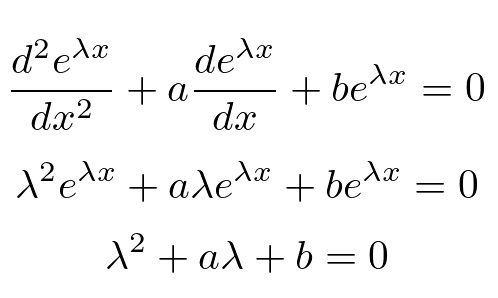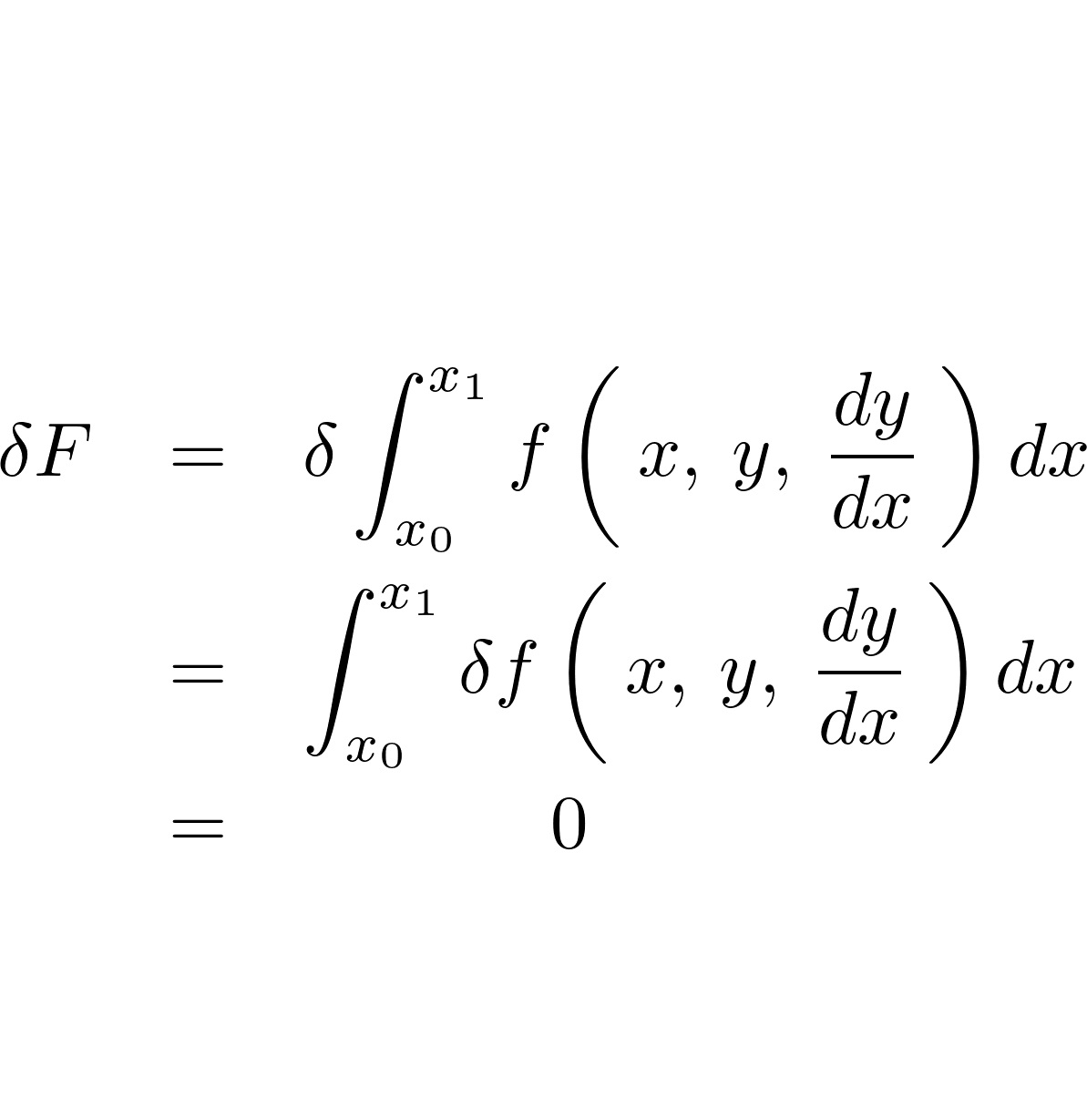コリオリ弾道軌道計算①
コリオリ力を考慮した長距離弾道軌道計算 ━ ①
“コリオリ”というのは地球が回転することによっておこる見かけの運動力を、回転座標上で移動したときの移動方向と垂直な方向に受ける慣性力の一種を数式で表現したものになります。
実際の現象で有名なのは台風の回転する向きなどで、それ以外には射程数キロをこえるような長距離狙撃などを行う場合はこのコリオリ力の影響を考慮する必要があり、よくマンガやアニメなどでその題材にされることもあるようです。
ちなみに余談になりますが、このコンテンツを作成しようとしたそもそものきっかけは攻殻機動隊というアニメでその主人公草薙素子(少佐)が放った言葉、「(敵が)コリオリ弾道を熟知した手練れ~」というのがもとになっおり、実際にコリオリを考慮した場合の軽火器の弾道計算をしてみようとしたのが始まりになっています。
以下の数式は回転座標系における見かけの運動力も考慮した運動方程式になります。
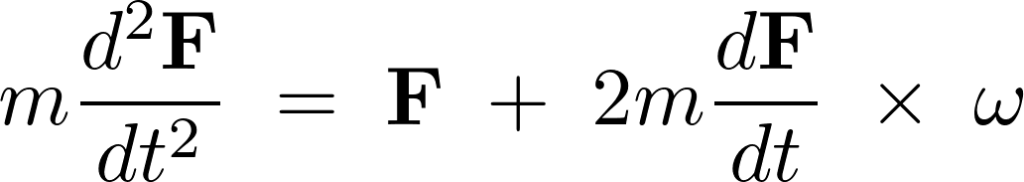
右辺第2項と第3項にあるのがその見かけの運動力を示す部分になり、2項と3項の間にあるバッテンは掛け算のバッテンではなく外積(クロスプロダクト)の表示です。この外積に関しての説明はこちらのサイトを参照してみてください。 今回は具体的にその弾道計算を代数的にやってみようと思います。
地球の回転速度

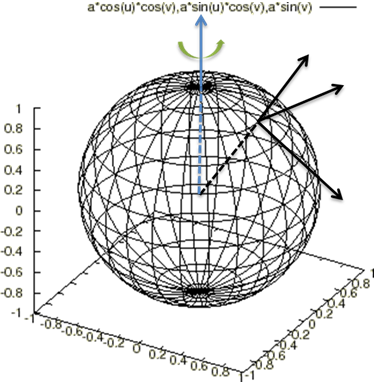
左の図のように地球に見立てた球体の北半球側の角度(緯度)を![]() で表しその角度における地表面の点を
で表しその角度における地表面の点を![]() 点、図のように地球の中心点から
点、図のように地球の中心点から![]() 点を通りその鉛直方向に延びる向きを
点を通りその鉛直方向に延びる向きを![]() 軸、そして南極点に向かう方向で
軸、そして南極点に向かう方向で![]() 軸とは直角方向の向きを
軸とは直角方向の向きを![]() 軸、そして東の方向(回転する方向)の
軸、そして東の方向(回転する方向)の![]() 軸、
軸、![]() 軸の両方ともから直角の回転方向へ向かう軸を
軸の両方ともから直角の回転方向へ向かう軸を![]() 軸とします。
軸とします。
さらに地球の回転速度(自転速度)を![]() と表します。
と表します。
三角関数などを使って三方向の角速度を表せば次のようになります。
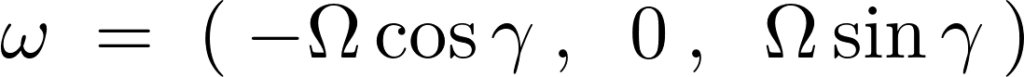
ここで外積の部分、
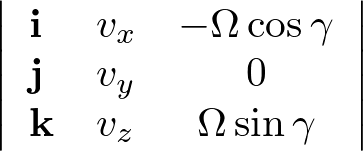
を具体的に計算していきます。
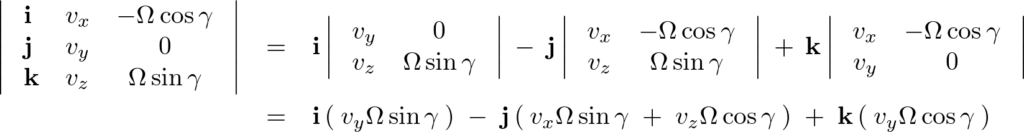
よって三方向それぞれの式は、
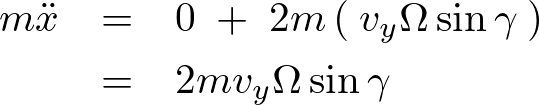
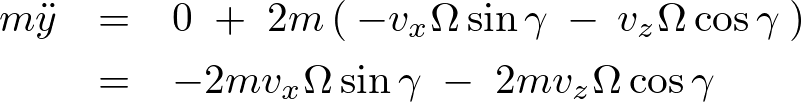
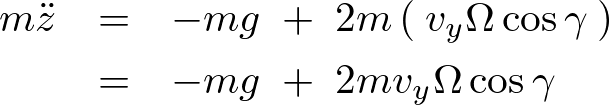
![]() を消してライプニッツ表記にしてまとめると次のような式が求められます。
を消してライプニッツ表記にしてまとめると次のような式が求められます。
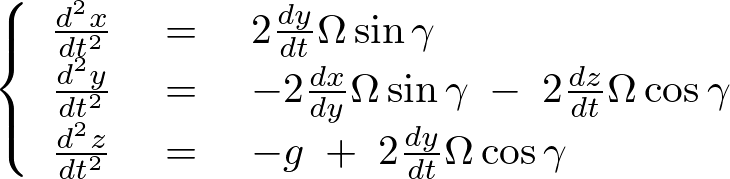
上記の式だと2階微分の項が入っているので積分を行って階数を一つ減らしてみます。
一回積分します。
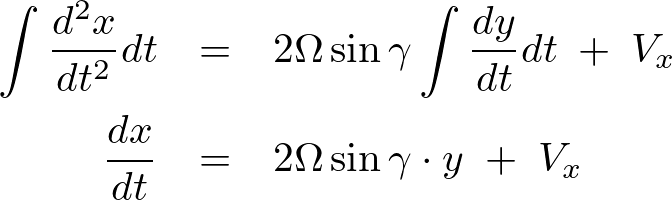
加速度成分に関して一度積分していますので出てきた![]() 方向における弾丸の初速度と考えられるので上記のように
方向における弾丸の初速度と考えられるので上記のように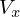 と表します。
と表します。
次に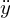 に対しても同様に計算をしていきます。
に対しても同様に計算をしていきます。
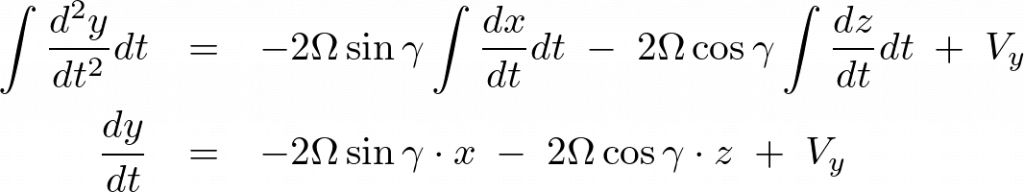
![]() に対しても同うように計算していきます。
に対しても同うように計算していきます。
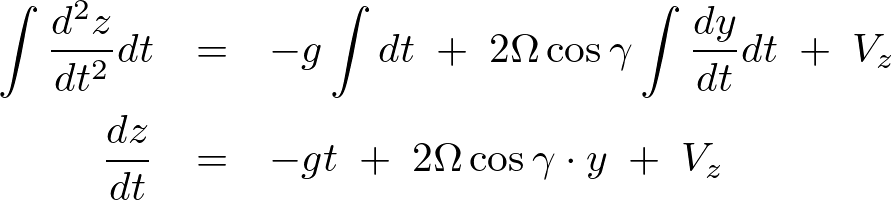
ここで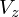 の成分ですが本来銃弾の射出においては照星を基準にして(標的までの距離を基準にして)照門の位置を上下にずらして弾丸を上方に向けて撃つものなのですが、ここではあくまで
の成分ですが本来銃弾の射出においては照星を基準にして(標的までの距離を基準にして)照門の位置を上下にずらして弾丸を上方に向けて撃つものなのですが、ここではあくまで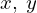 軸に水平に射出するものと仮定するのでそれを無視します。
軸に水平に射出するものと仮定するのでそれを無視します。
なのでここでは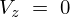 とします。
とします。
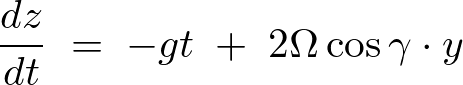
これらの連立微分方程式を解いていきますが、元の式をよく見てみると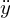 の式の中に
の式の中に![]() と
と![]() のそれぞれの一階微分の項が入ってるのでこれに代入して連立方程式のように計算していったほうがよさそうなのでそのままやっていきます。
のそれぞれの一階微分の項が入ってるのでこれに代入して連立方程式のように計算していったほうがよさそうなのでそのままやっていきます。
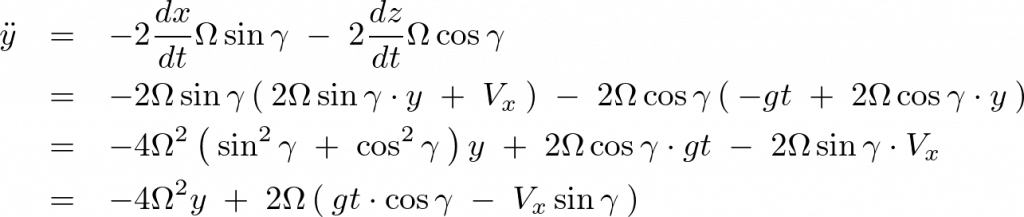
結果的に次のような連立微分方程式を解いていくことにします。
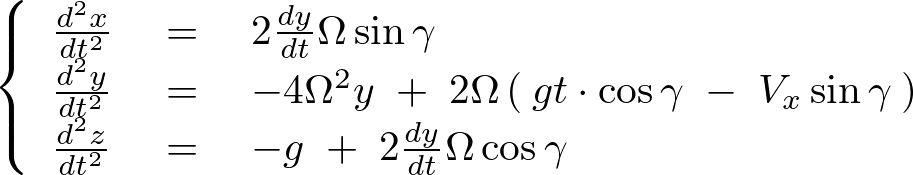
コリオリ弾道軌道計算②へ続きます。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-

ラプラス変換
カテゴリー
-
2024年6月8日マイグレーション完了
カテゴリー
-
フェルマーの原理
カテゴリー
-
エルミート関数
カテゴリー
-
フーリエ余弦正弦展開
カテゴリー
-
フーリエ変換
カテゴリー