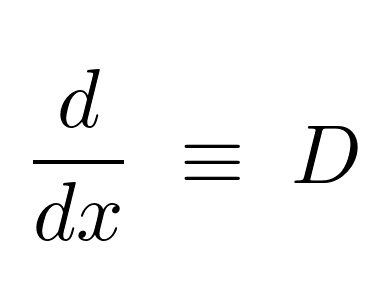階段関数のラプラス変換(査読および作成編集中)
ヘヴィサイドの階段(単位)関数
次のような性質をもった関数を考えます。
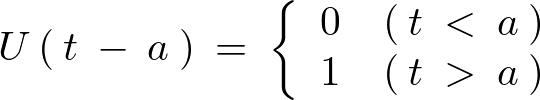
この階段関数をラプラス変換する場合、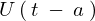 は
は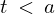 で
で で、
で、 で1であることを考慮すると、
で1であることを考慮すると、
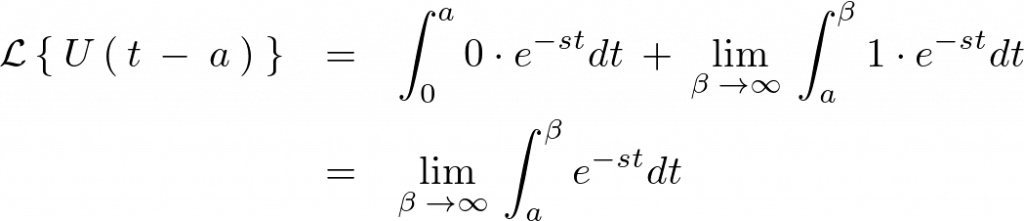
これを計算していくと、
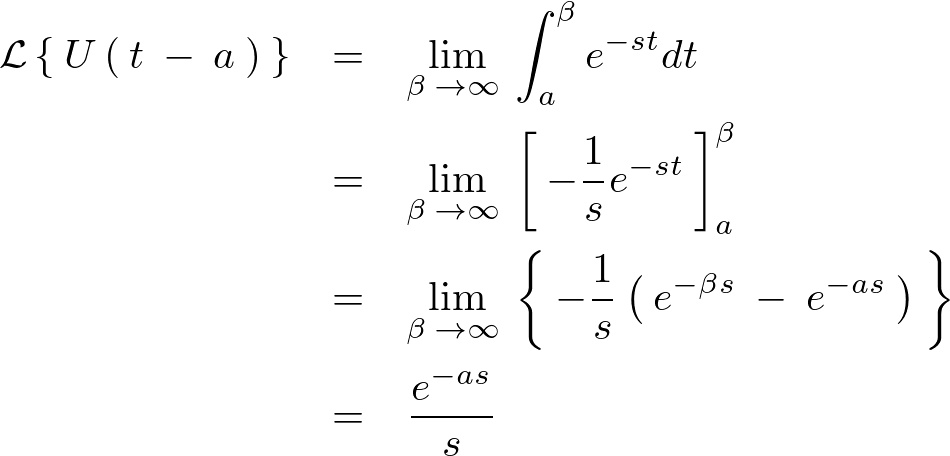
この結果により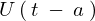 のラプラス変換は
のラプラス変換は![]() が
が 以下のとき
以下のとき![]() で発散し
で発散し 以上のとき以下のようになります。
以上のとき以下のようになります。
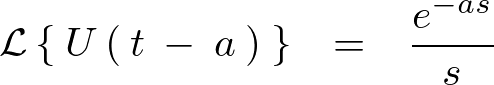
ここで複素数![]() に関して実数部を
に関して実数部を![]() とおいて、虚数部を
とおいて、虚数部を![]() と置きます。
と置きます。
そうすると、上式の右辺に関して、
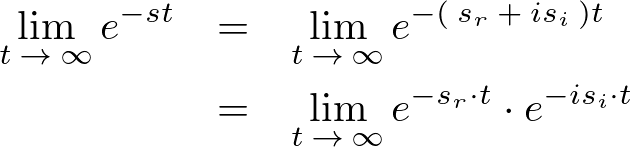
さらにここで三角関数の公式を使えば、
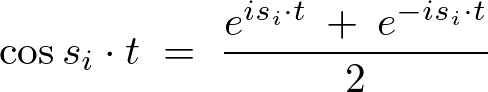
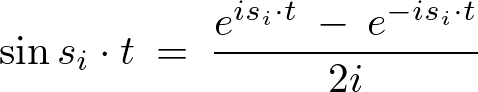
これを引き足しすれば以下のような関係式が求まります。
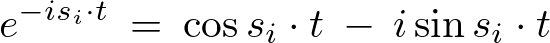
これを使えば、
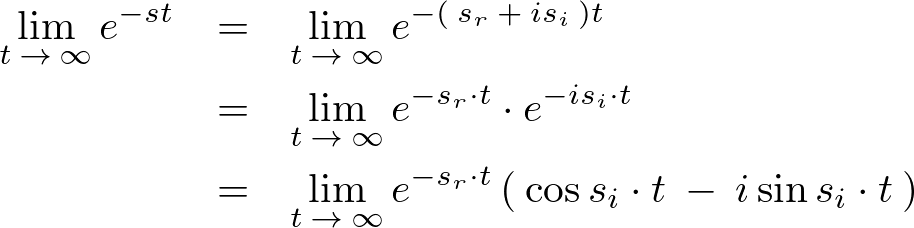
このラプラス変換が存在するためには三角関数の絶対値が1以下であることを考慮すれば次のような条件が決められます。
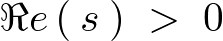
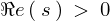 の
の は複素数で実数部を意味します。
は複素数で実数部を意味します。
この階段関数を使うことによりある関数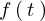 に関して区分的に分けるということができ、またこういった性質は何ステップにもわたって作ることが可能になります。
に関して区分的に分けるということができ、またこういった性質は何ステップにもわたって作ることが可能になります。
例えば次のような表現も可能になります。
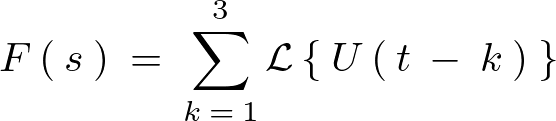
実際にこれを計算していきます。
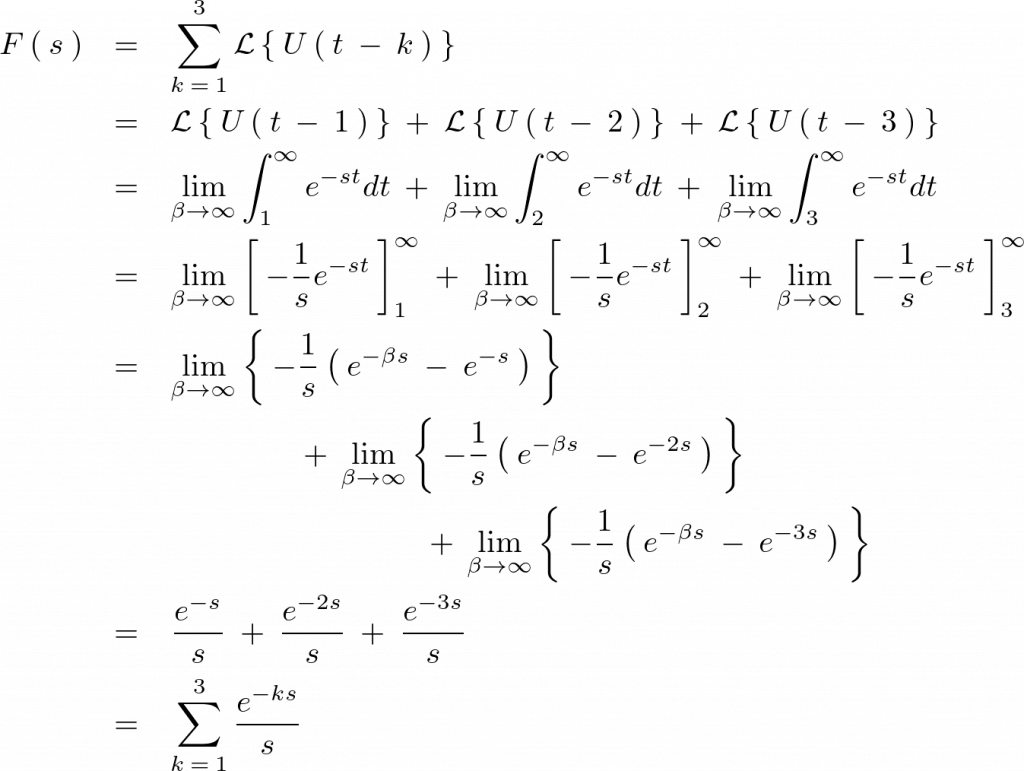
ここで次のようにおきます。
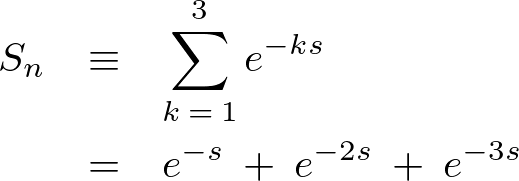
さらに次のようにおきます。
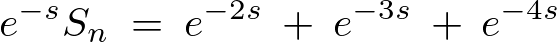
辺々足し引きすれば、
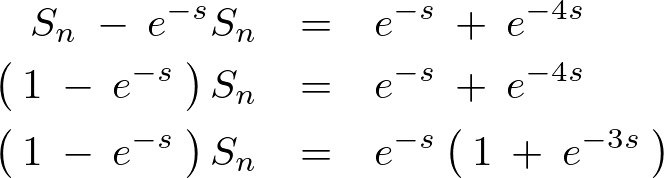
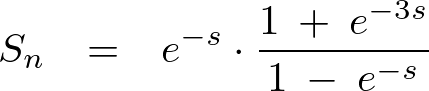
代入します。
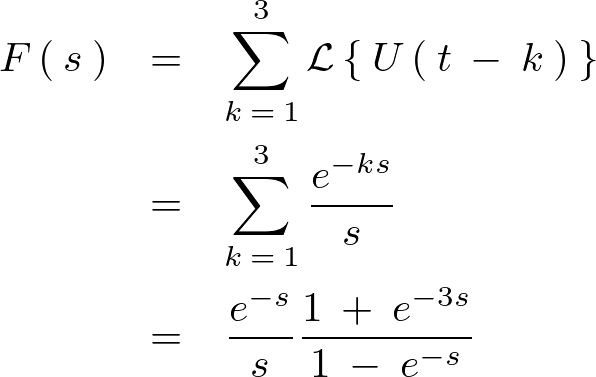
となるので階数が3のヘヴィサイド階段関数のラプラス変換は以下のように求まります。
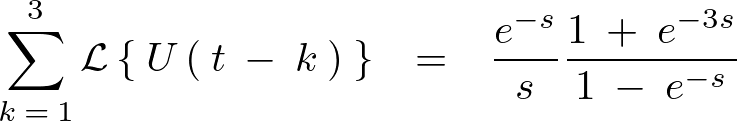

ラプラス変換の移動法則
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
-
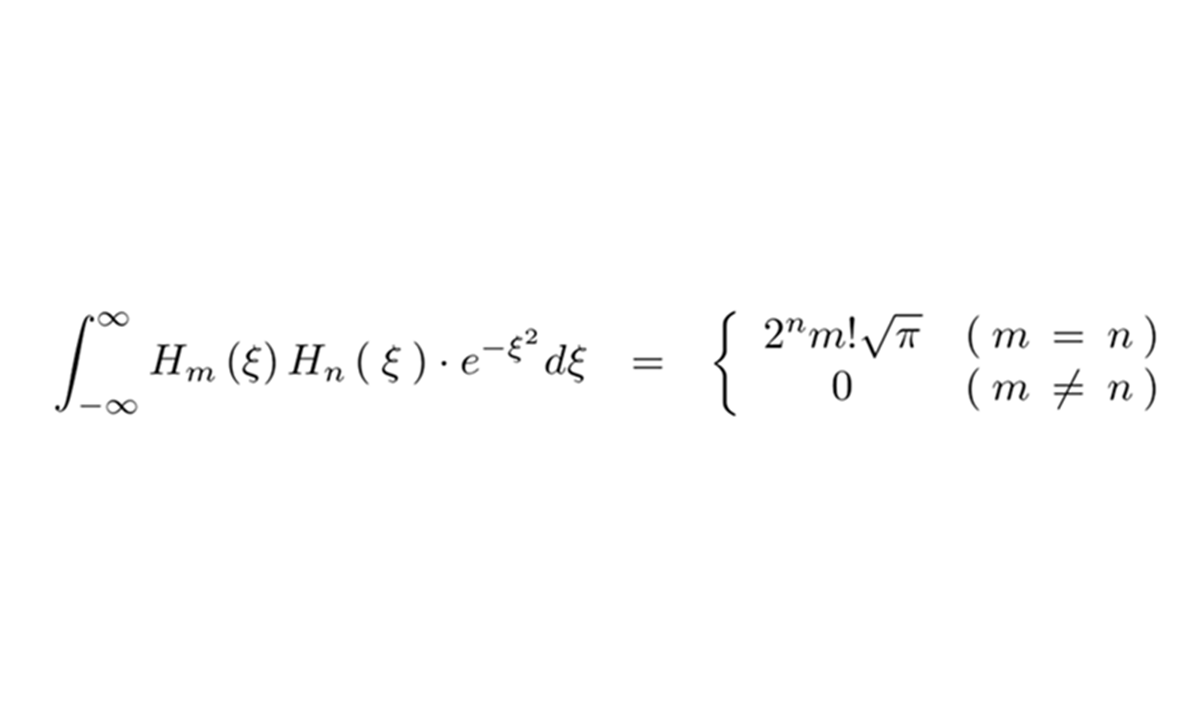
エルミート多項式の直交性
カテゴリー
-
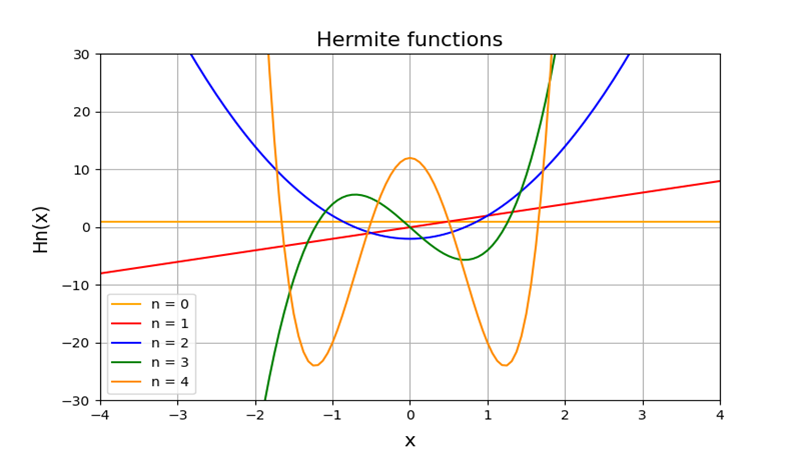
エルミート多項式の諸性質
カテゴリー
-
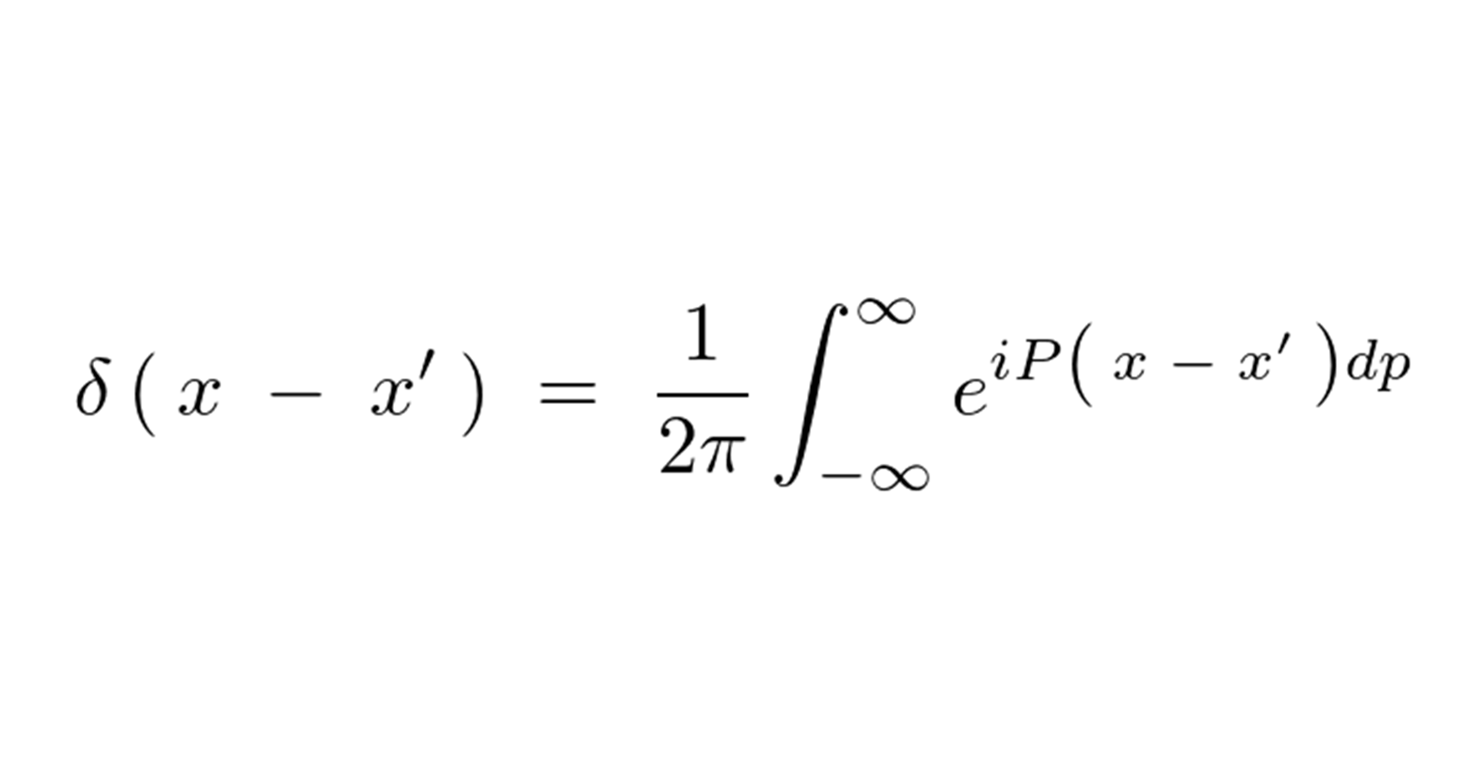
デルタ関数のフーリエ変換
カテゴリー
-
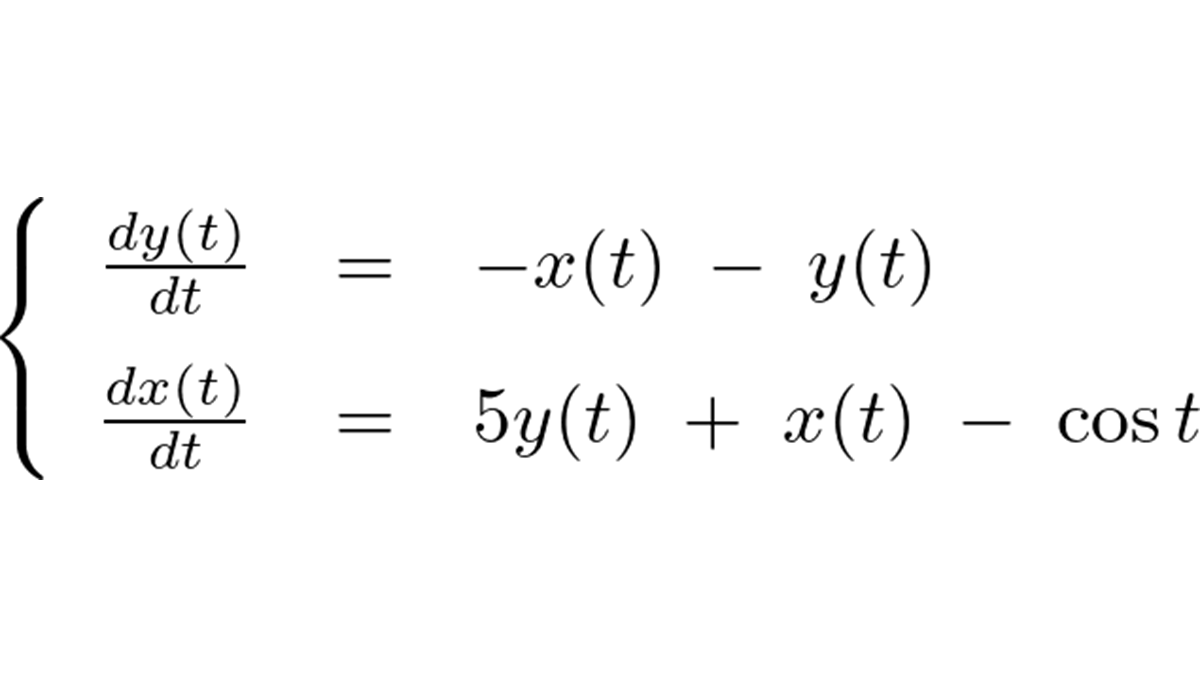
連立微分方程式の解法②
カテゴリー
-
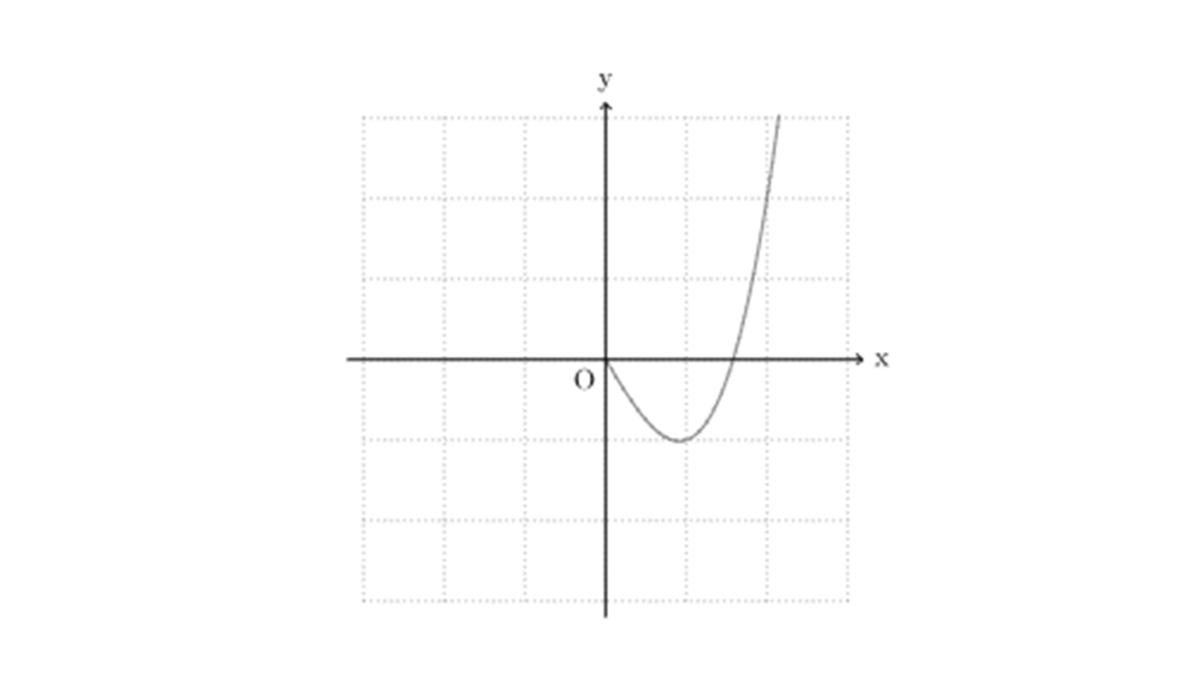
ヘヴィサイドの階段関数
カテゴリー
-
コリオリ弾道軌道計算③
カテゴリー
-
-
-
-
-
-
-
-
-
-
微分演算子による連立微分方程式の解法①
カテゴリー : 微分演算子による連立微分方程式の解法①オペレータ作用素をD=d/dtのようにおき、それを代数的に取り扱うことによって連立微分方程式の解をシステマティ…