黒体放射とヴィーン変位則とは
ヴィーンの変位則とは、黒体と呼ばれる光などの電磁波をすべての波長において吸収またはそれを放出(反射)できる理想的な物体のことをさし、その黒体からの輻射波長が温度に反比例するという法則になります。このセクションではこれをプランクの式を使って考察していきます。
ビックバン理論
CMB:Cosmic Microwave Backgroundの発見
1960年代前半から宇宙背景放射を検出しようとし、1989年 COBEの打ち上げにより黒体放射を発見。 宇宙背景放射に対する因果律の説明は、恒星の光が塵などの物質によって反射されるなどして銀河内にとどまったものと考えられましたがこれだと方向による背景放射強度の“揺らぎ”が非常に滑らかであることの説明が難しく、更にはこの宇宙背景放射が黒体放射に極めてよく一致するということなどによりやがてビッグバン宇宙理論が注目されることになります。
ヴィーンの変移則と黒体放射
黒体というのは光などの電磁波をすべての波長において吸収またはそれを放出(反射)できる理想的な物体のことを言います。こうした性質を完全に持つ物体を完全黒体といいますが厳密にそういったものは存在しないといわれてます。 この黒体によって放射される電磁波を黒体放射といい放射される電磁波の波長を![]() 、温度を
、温度を![]() とおくと波長λでの黒体放射の式はプランク定数をh、cを光速、ボルツマン定数をkとすれば次のように表されます。
とおくと波長λでの黒体放射の式はプランク定数をh、cを光速、ボルツマン定数をkとすれば次のように表されます。
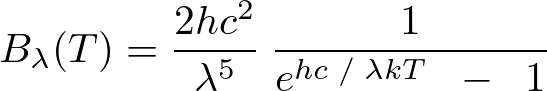
このある波長λでの黒体放射の式を次のようにおきます。
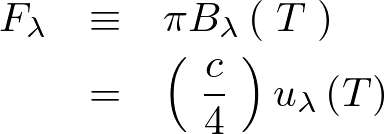
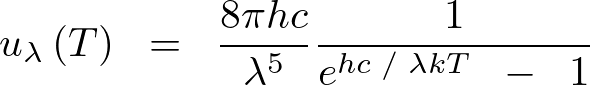
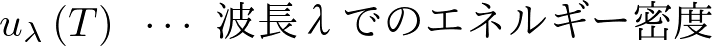
このエネルギー密度の式に対してλで偏微分を実行し、さらにそれに対して極値をとります。
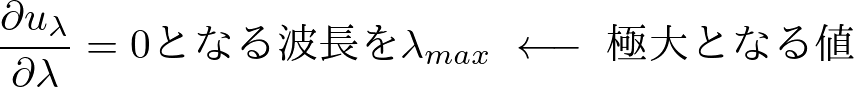
この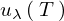 の式を、
の式を、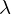 で微分していきます。
で微分していきます。
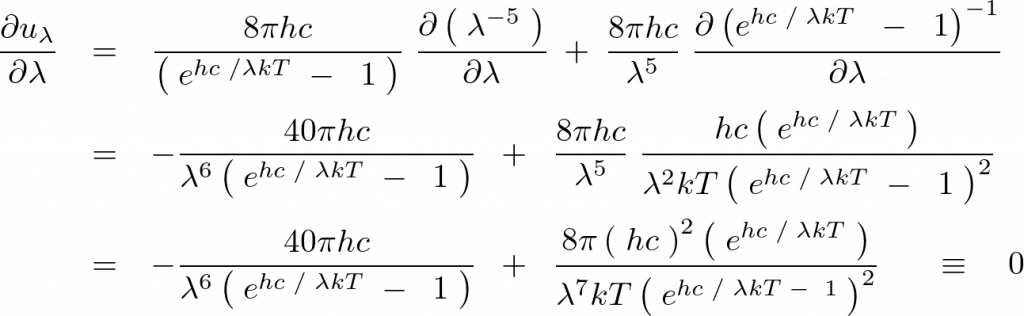
ここで上記の式全体を見やすくするために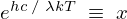 と置きます。
と置きます。
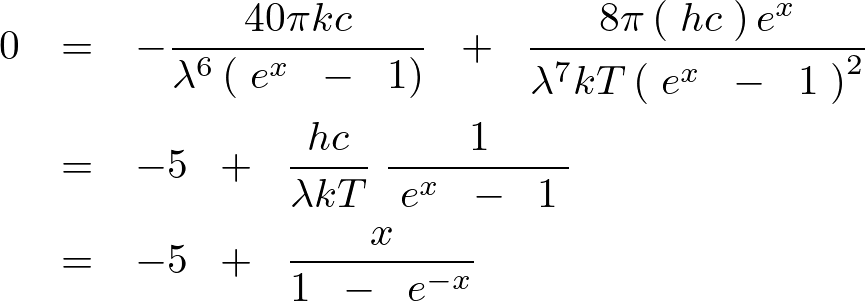
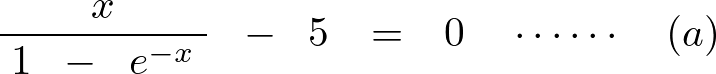
この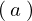 の式を解いていきますがこの方程式は
の式を解いていきますがこの方程式は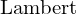 の
の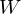 関数と呼ばれるものを使って解いていきます。この
関数と呼ばれるものを使って解いていきます。この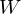 関数というのは、
関数というのは、
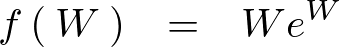
と表すものであり、任意の複素数![]() に対して次のような式が成立します。
に対して次のような式が成立します。
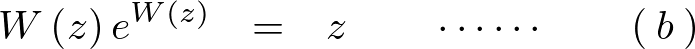
解き方としては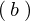 の式の左辺のような形にすれば右辺の
の式の左辺のような形にすれば右辺の![]() が求まるという要領らしいです。
が求まるという要領らしいです。
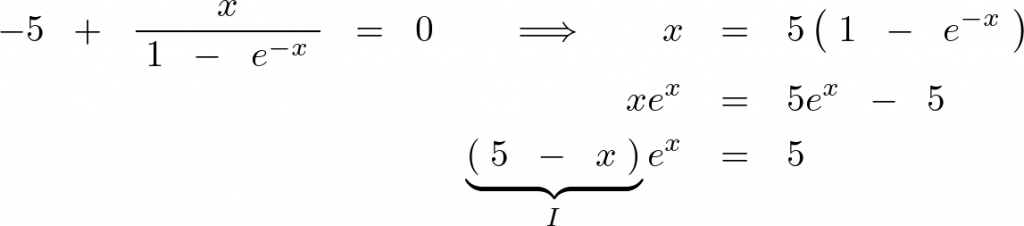
ここで両辺に![]() をかけ、イクスポーネンシャルの乗数の部分と“
をかけ、イクスポーネンシャルの乗数の部分と“![]() ”の部分を同じ形にします。
”の部分を同じ形にします。
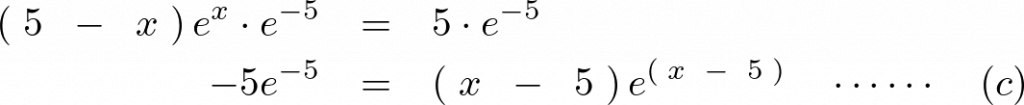
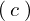 より、
より、
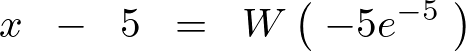
となるので整理すれば、
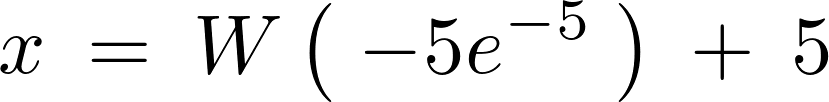
この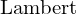 の
の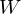 関数に関してはマテマテカのサイト、
関数に関してはマテマテカのサイト、
https://mathworld.wolfram.com/LambertW-Function.html
などのWebサイトを参考にしてみてください。
そしてこの数値解析の結果を代入して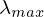 を求めると、
を求めると、
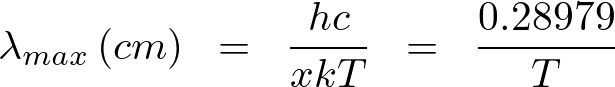
よって波長の最大値における温度Tとの関係式は近似をして、
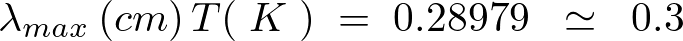
これをヴィーンの変位則といいます。
【例】 の星の場合
の星の場合
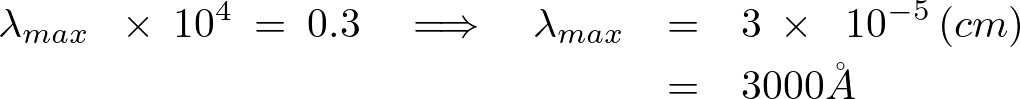
また、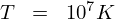 においてでは、
においてでは、
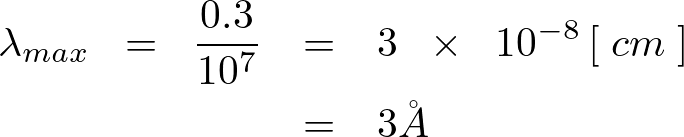
黒体放射とヴィーン変位則
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

シュテファンボルツマン法則
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

宇宙基礎方程式とパラメータ
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.

フリードマン宇宙モデル①
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.