フェルマーの原理とは

幾何光学における基礎的原理

フェルマーの原理というのは媒質中（屈折率は一定とします）を通る光の２点間の通過時間は極小になるような経路をとるというものであり、幾何光学においては基礎的な理論になります。ここではこれに関して変分法を使って表してみましょう。
曲面を記述する独立な２つのパラメーターを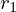、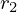とします。そのときのベクトル方程式は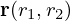であり、さらにこの方程式に対してのパラメーターをとすれば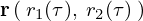となります。

この線上での距離だけ進むとき、そのは次のよう表せます。

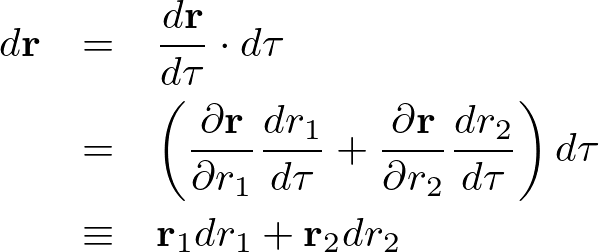
ここでベクトル表記を次のように集約します。

こうすることにより次のようになります。

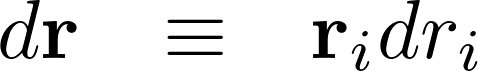
これらを用いれば、

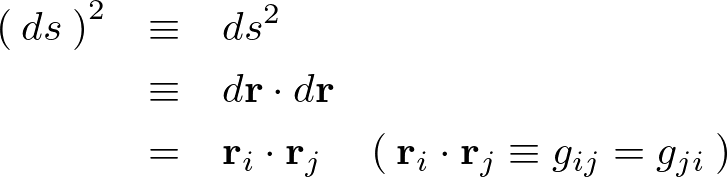
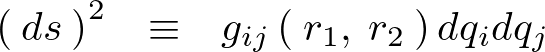
媒質中点における屈折率を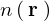とし、真空中における光の速さを、における光の速さを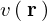、経路のパラメーターをとします。

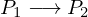への移動にかかる時間は、

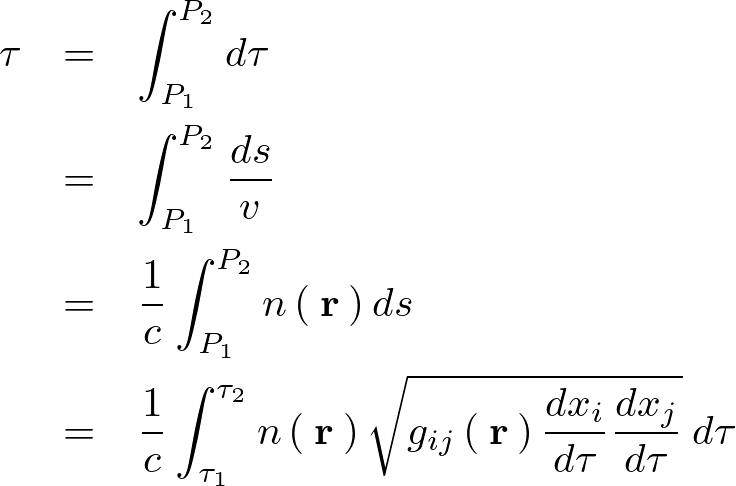
これによってフェルマーの原理は次のようになります。

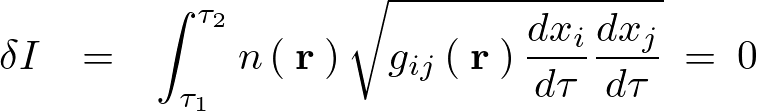
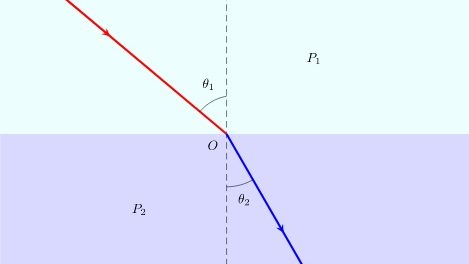
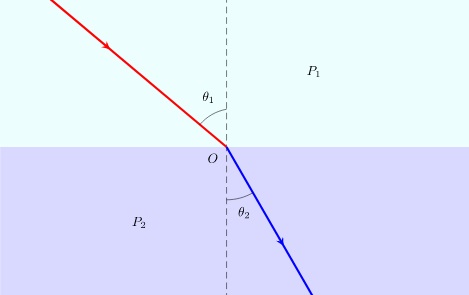
絶対屈折率が、の媒質が平面で接している場合、一方の媒質からもう一方の媒質へ光が通過する場合を考えてみます。

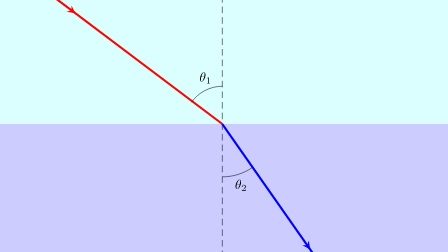
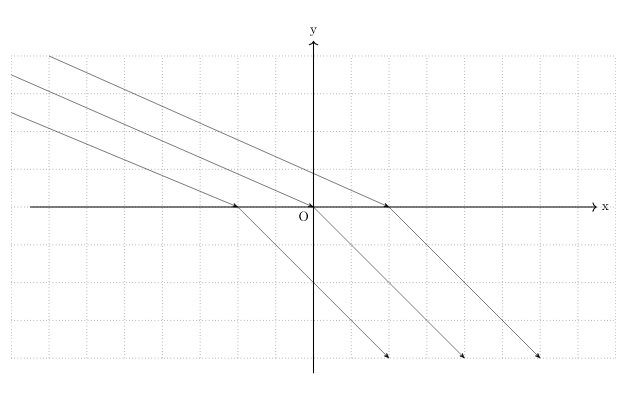
図は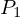の位置から境界面上の点を通過し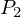に至るものとします。
ここでは屈折率により変わるので以下のように表すとします。

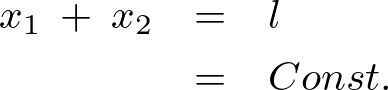
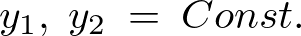
一定の媒質中であるならば経路は直線なので、

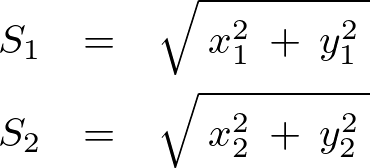
これにより、

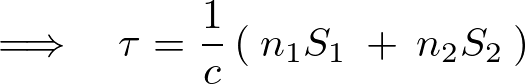
一方、拘束を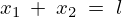としそれを代入すると、

について変分をとると、

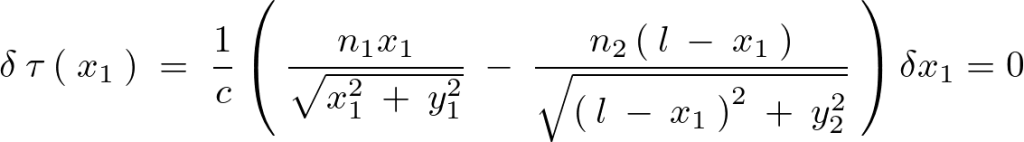
ここでと戻せば、

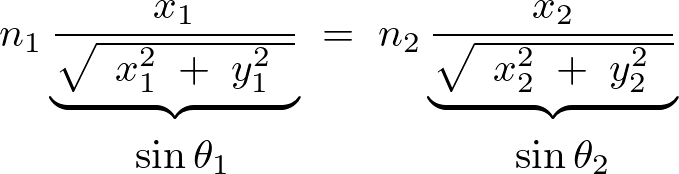
この結果によって次のように表すことができます。

光の進む経路が最小になるように進むというフェルマーの原理からきていますがこれは一般的にはスネルの法則などという呼び方もします。