オイラーの式

ある関数の積分、

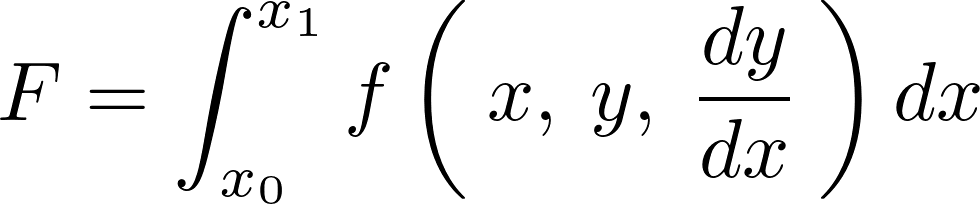
があるとします。

この差異を考えて、この時の変位をとするとこれが極致を持つ条件というのは、

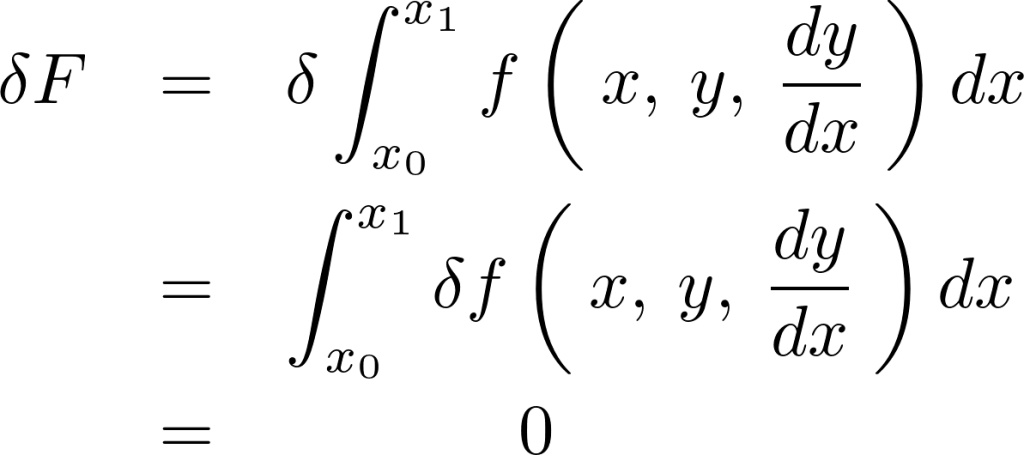
をちょっとだけ動かしたものを、

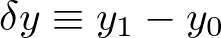
その導関数の変分をとると、

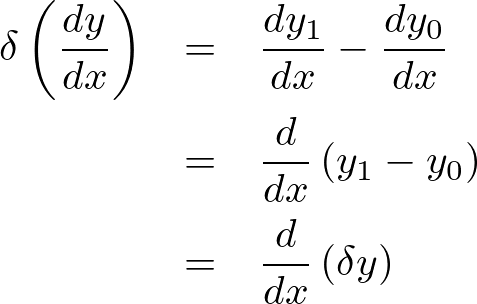
微分と変分は入れ換えることが可能であるとします。

さらに、関数に対して全微分の公式を適用すると、次のようになります。

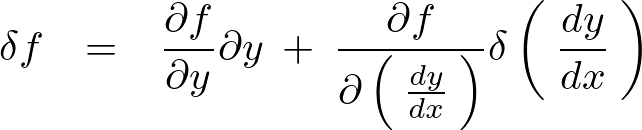
上記の式に対して、以下の式、

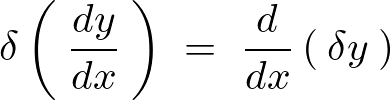
を適用すると次のようになります。

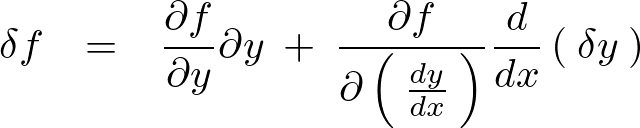
さらに先ほど出てきた、

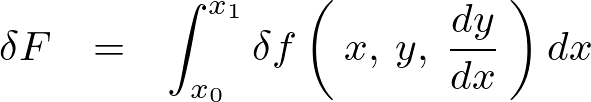
を適用すると次のようになります。

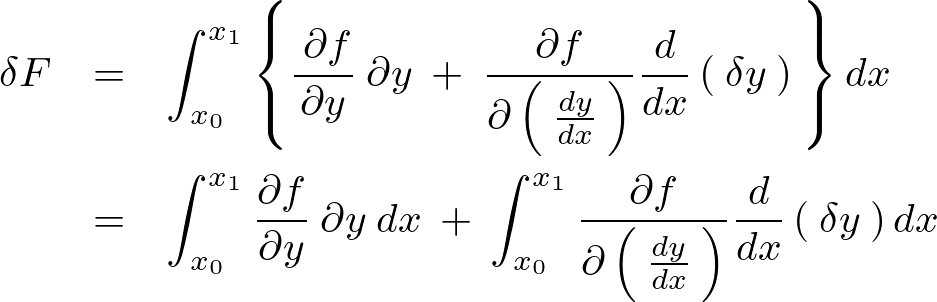
上記式を計算していきます。

右辺第２項の積分計算に関しては以下のように部分積分を使います。

ここで上式の部分積分を施した右辺第一項は、端点を固定（同じポイント）しているので結果は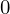になります。

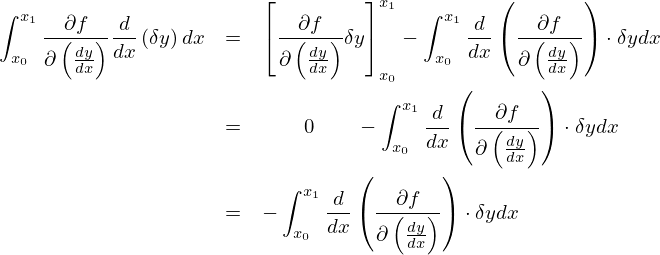
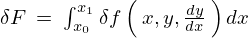に代入していきます。

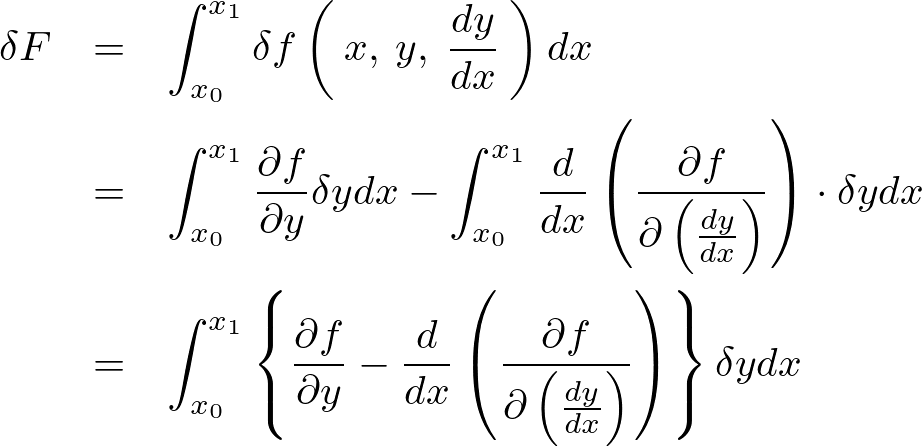
そしてこの積分がに対して結果がとならなければならないので次のようにおくことができます。

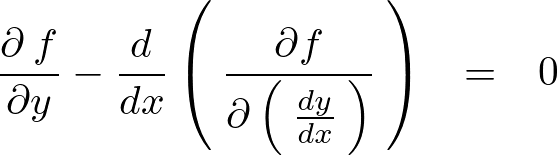
これがオイラーの方程式、またはオイラーラグランジュ方程式と呼ばれているものになります。