2重振り子の振動②-微小でない場合

微小でない場合の２重振り子の振動

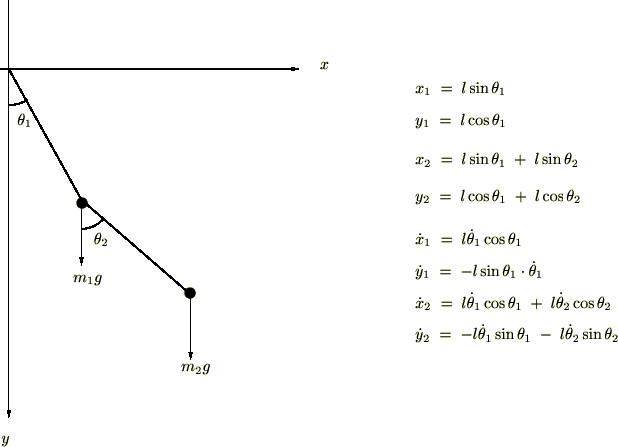
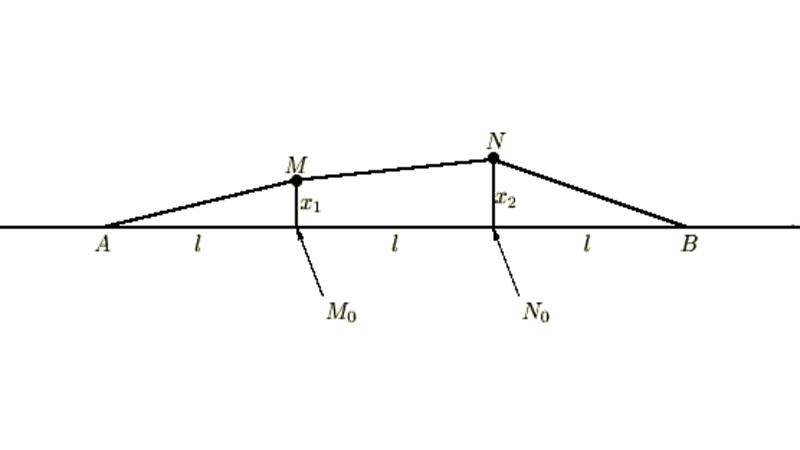
上図のそれぞれのおもりはどちらも質量をとし、その重りをつないでいる糸の長さはで曲がったりせずかつ重さは無視できるものとします。

軸に関しては下向きにとります。

こうした場合、ラグランジアンの式は次のような式になります。

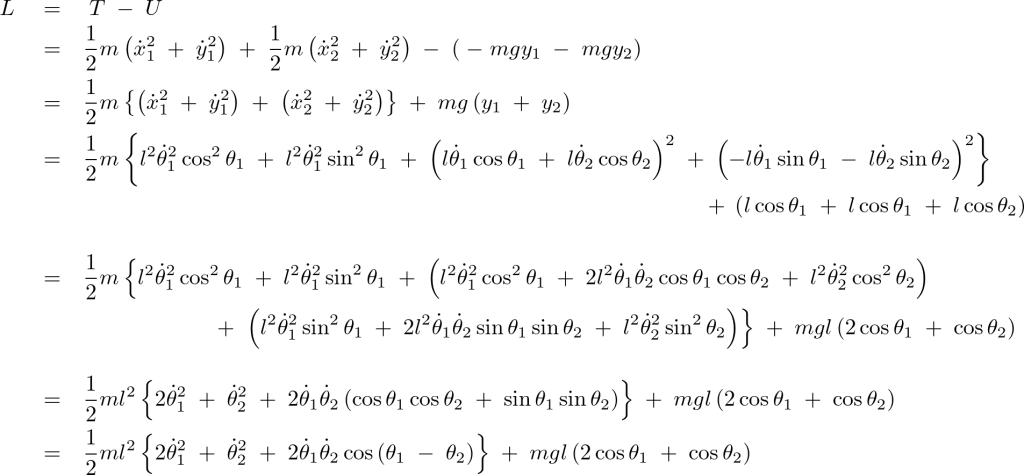
途中の式では以下のような三角関数の公式、

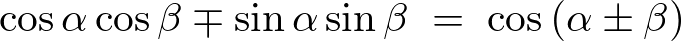
を使っています。

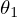についてのラグランジアンは、

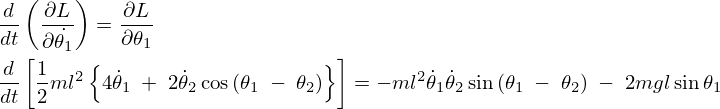
ここで三角関数の公式を使うと、

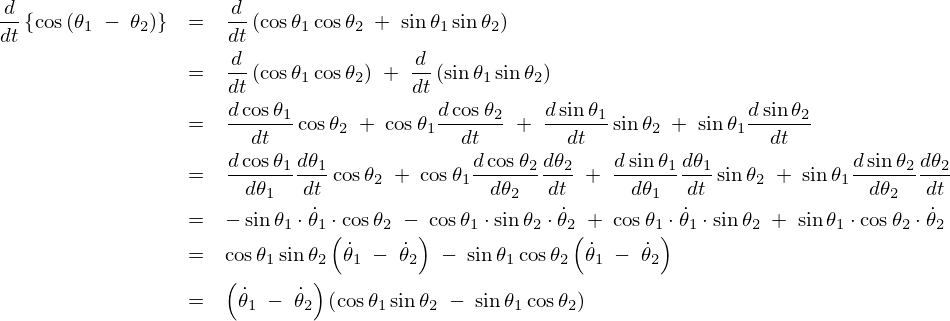
ここで求まった上記式に対して以下の三角関数の公式を適用します。

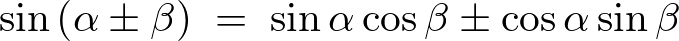
そうすると以下のように求まります。

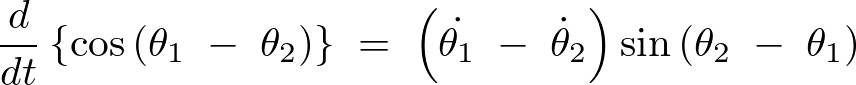
この結果を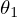についてのラグランジアンに使えば、

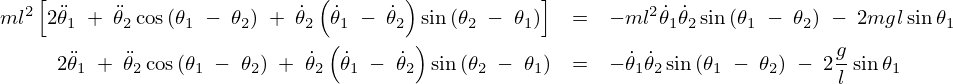
次はに対しても同じようにすると、

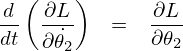
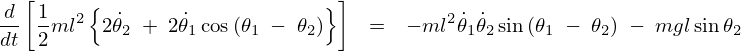
となるので以下のように求まります。

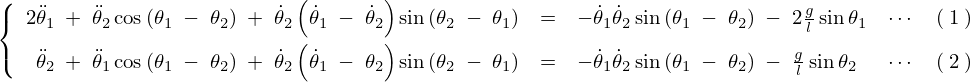
上記の式に関してそれぞれ、のそれぞれについて求めていきます。

まず上記式に関して、

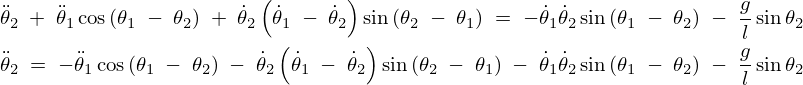
出てきたこの式を式に代入すると、

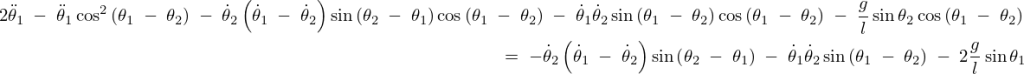
さらに計算していきます。

これによりに関しては以下のように求まります。

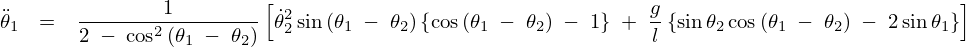
また上記式導出においては三角関数におけるの性質であるを使っています。

次にを求めます。

まず、式においてについて変形すると、

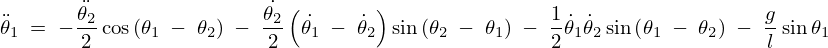
この式を、先ほどの、

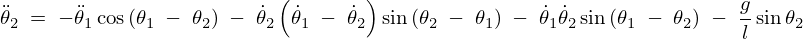
の式の右辺のに代入し計算していきます。

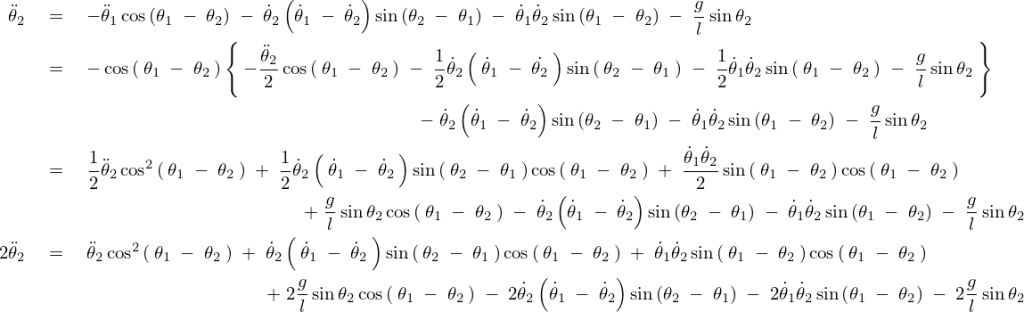
これより、

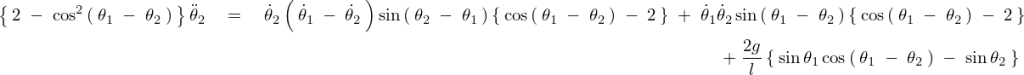
この式の右辺をさらに以下のようにして計算していきます。

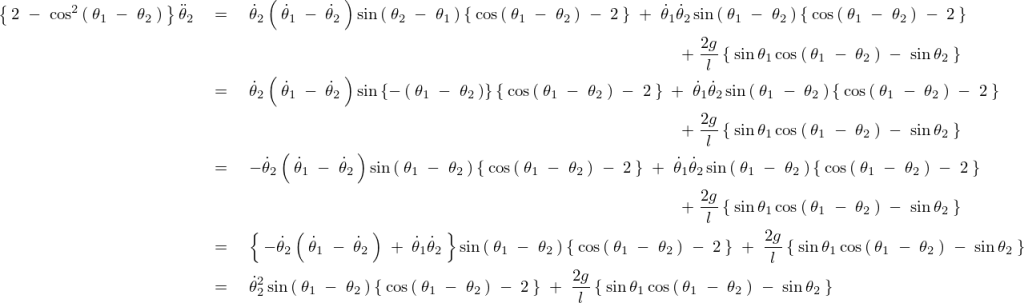
これによりは以下のように求まります。

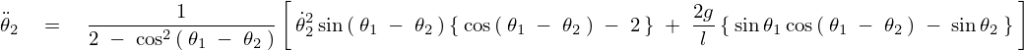
まとめれば以下のようになります。

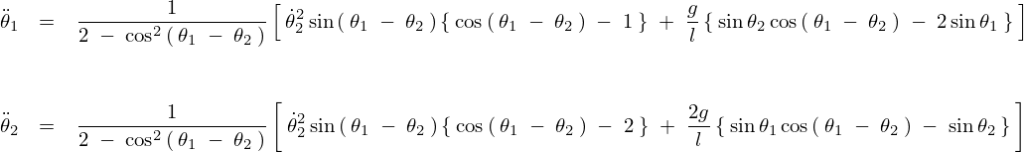
出てきた式を見てわかるように、かなり複雑な運動を行うことが予想できると思います。

さらにおもりの重さの違いや糸の長さの違いなどが加わればもっと複雑な、なかばカオス的な状態を導くことになります。

近似式を用いた振動の考察

いったんここで、上式において次に示す近似式、

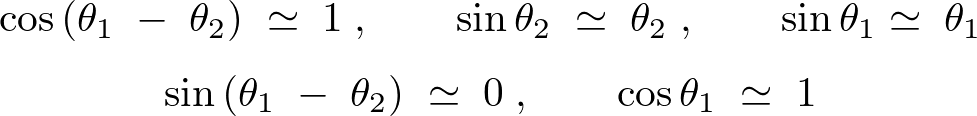
これらを代入して計算するとどうなるかを考察してみましょう。

まずより、

さらにより、

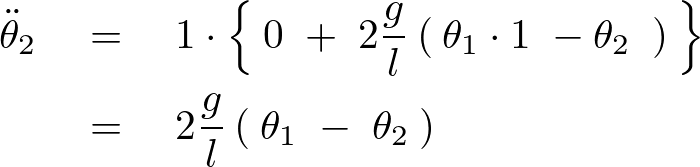
結果として次のような関係式が求まります。

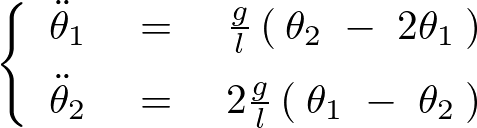
さらに今度は上記関係式を連立させて計算していきます。

まず、

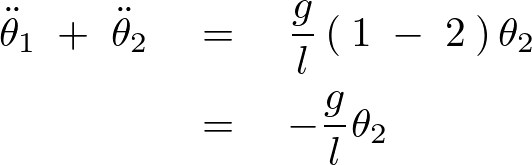
次にの式に関してそれを２倍して辺々かけ合わせます。

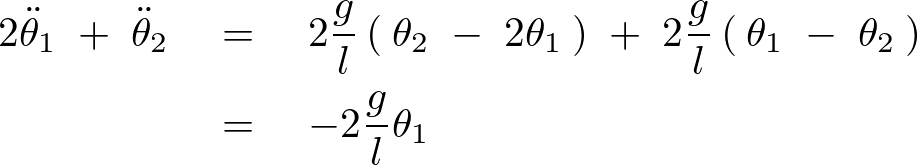
先ほどの複雑な２つの式が以下のように簡単な形式の連立微分方程式になります。

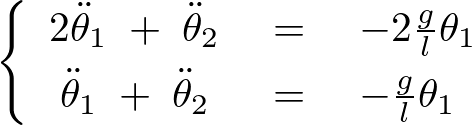
ここで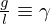とおいてみましょう。

すると、

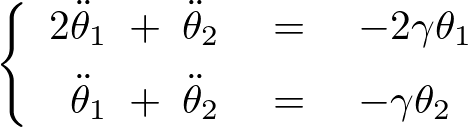
これは２重振り子の振動①-微小な場合において求められた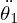、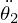の連立式と同一なものであることがわかります。