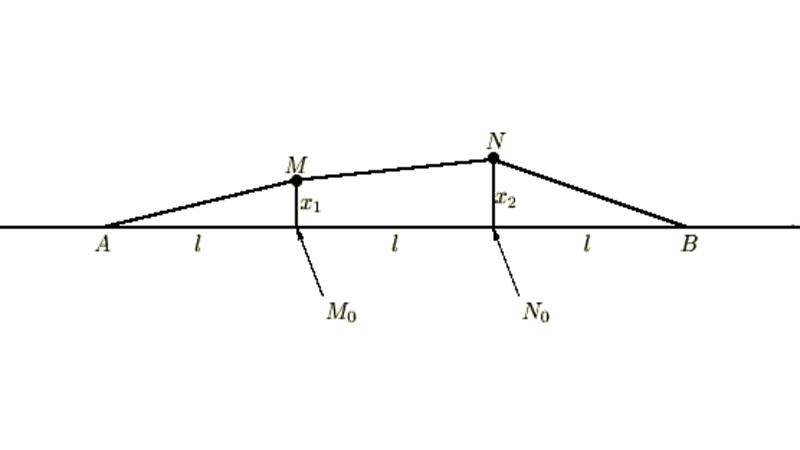
2重振り子の振動①-微小な場合

おもりを２つ吊るした振り子の微小振動の動きをラグランジアンを使って解析してみましょう。

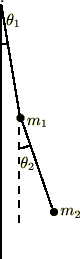
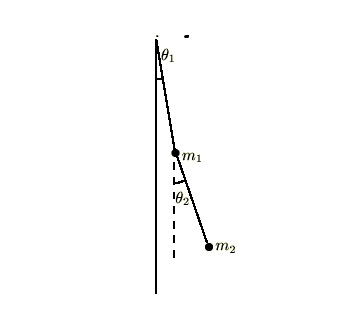
糸の重さは無視できるものとします。

微小振動としているので、

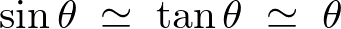
このような場合は水平方向のみを考えればよいです。

まず運動エネルギーは、

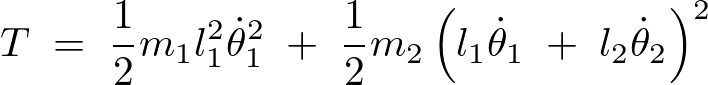
ポテンシャルエネルギーは、

とした場合となってしまうので、以下のように級数展開します。

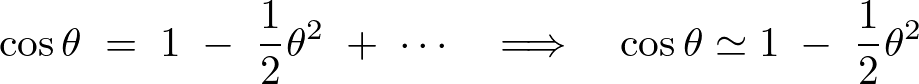
より、

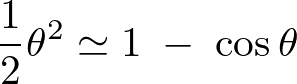
とします。

これを使えば、

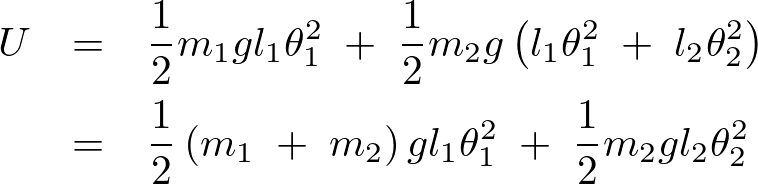
よってラグランジアンは次のようになります。

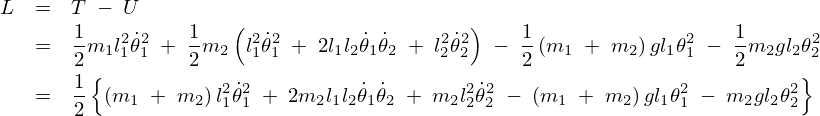
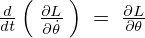より、

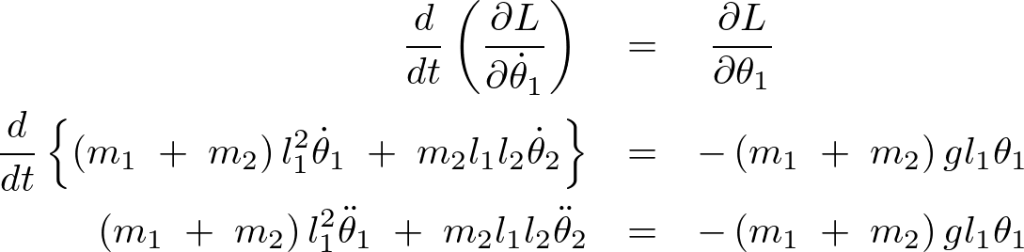
に関しても同様にして、

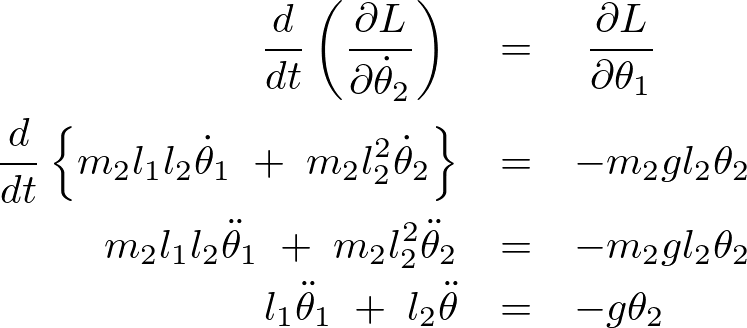
ここで、として見やすくすると、

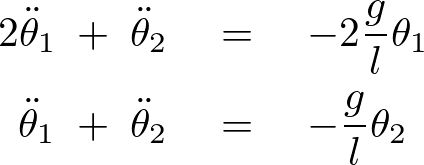
さらにとおけば、

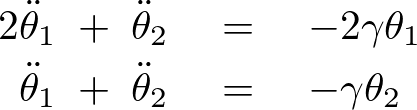
２つのおもりの角振動数を、初期位相をとし、解を次のように置きます。

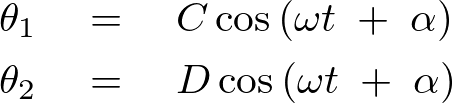
それぞれ２度微分すれば、

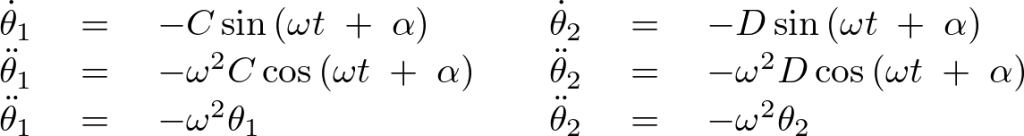
これらを、

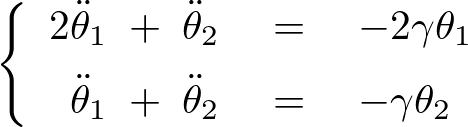
に代入します。

これより、

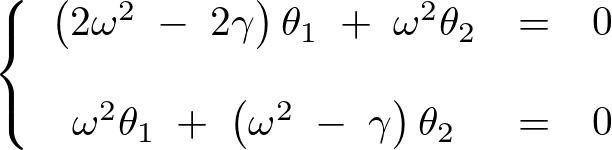
上記の式においてが同時ににならない条件を求めます。

その条件は永年方程式を使って次のようになります。

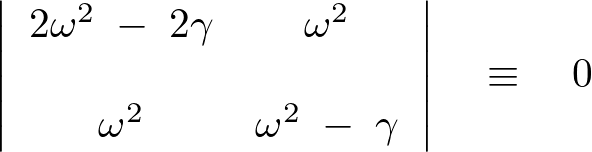
この行列式を計算します。

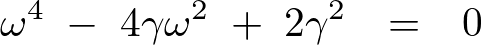
ここでとすると、

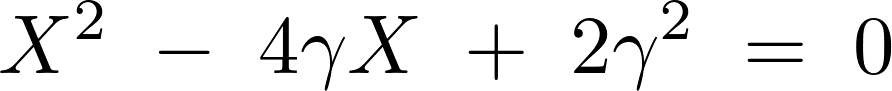
この上記方程式を解いていきます。

解の公式を使って求めると、

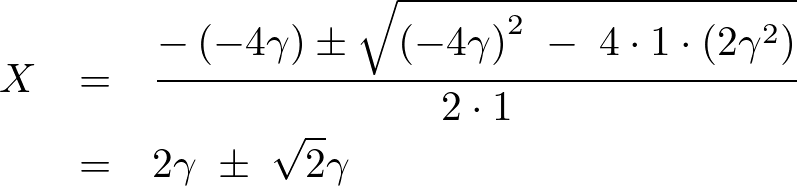
置き換えたをもとに戻せば、

以下のように求まります。

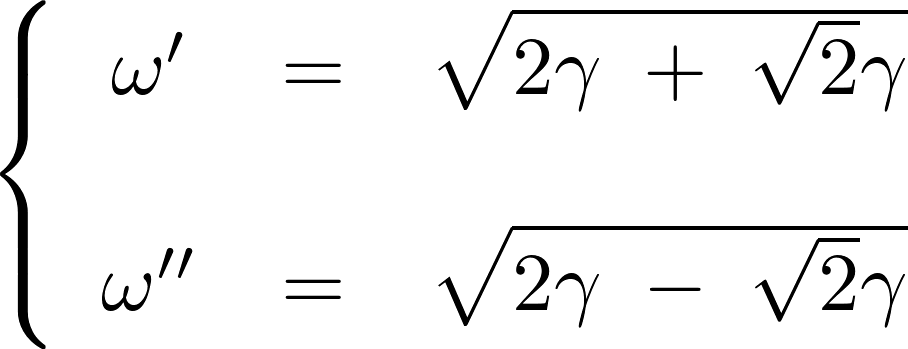
これが微小振動における２重振り子の基準振動数になります。