連成振動の解②

3重バネの振動

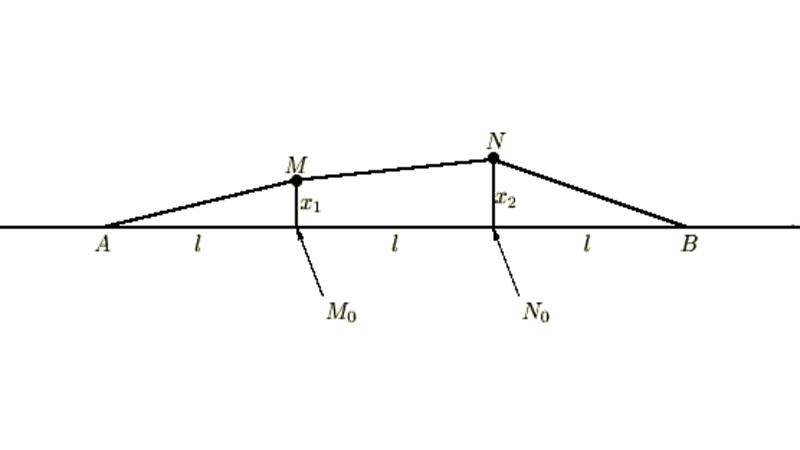
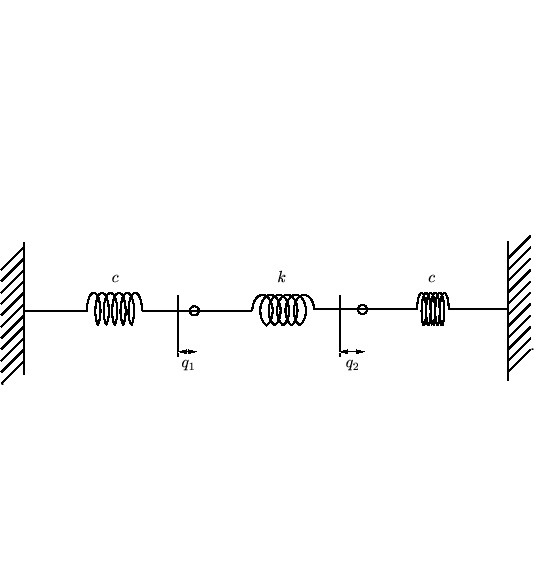
以下のような図において、壁側についているばねのばね定数を、真ん中のバネのバネ定数をとし、そのバネの境に重さのおもりをつけた場合の連成振動の解をラグランジアンを使って考察していきます。

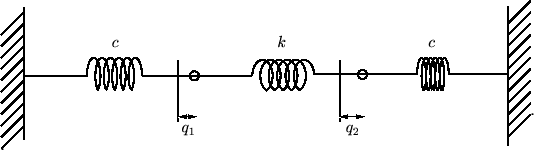
振動の方向は水平方向のみとし、両質点の変位を、とすれば左端のバネはだけ伸び、中央のバネはだけ伸び、右のバネはだけ縮みます。

こうしたときラグランジアンは、

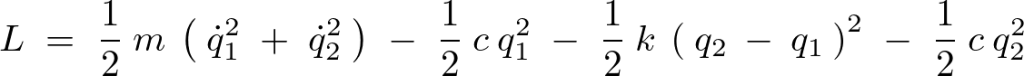
まず最初により、

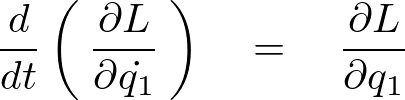
より、

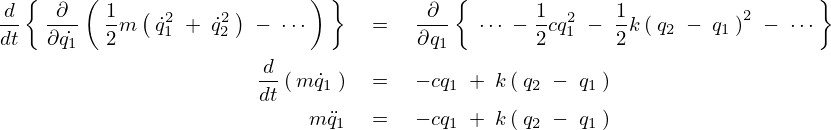
またに関して、

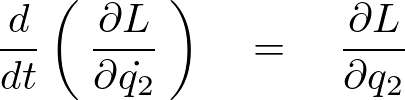
より同様にして、

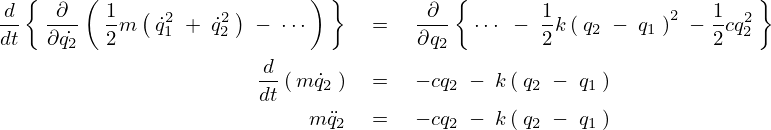
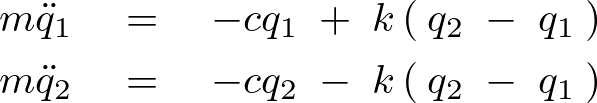
ここで上記方程式における、の解を次のようにおきます。

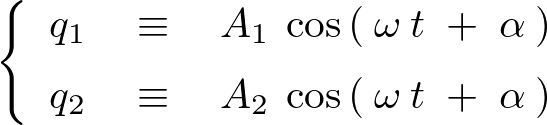
この両式に対して時間微分を施します。

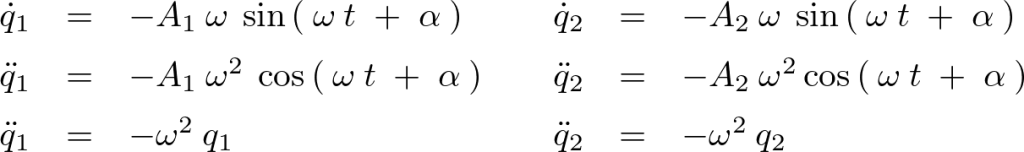
この時間微分による結果を代入していきます。

まずより、

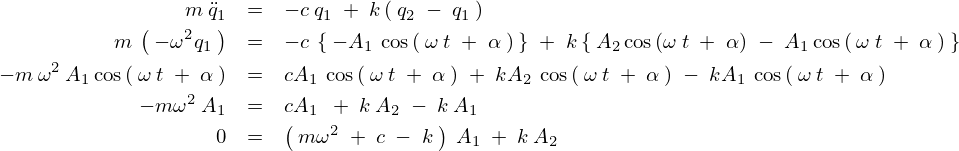
に関しても同様にして、

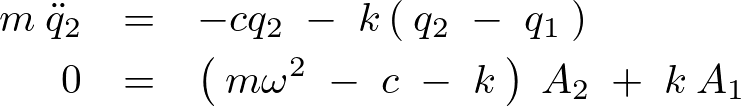
まとめれば以下のように求まります。

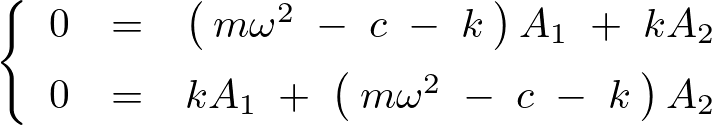
上記式においては、、が同時にになると運動しないことになります。

なので、およびのような運動が可能であるには、が同時に“”にならない条件として、 先ほどのセクション内において示した次のような式、

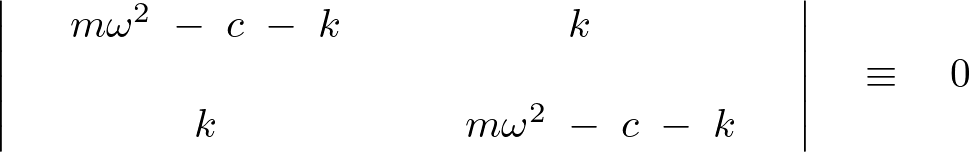
を考える必要があります。

これを実際に計算すると、

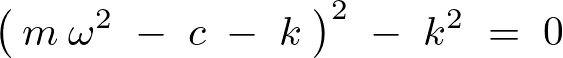
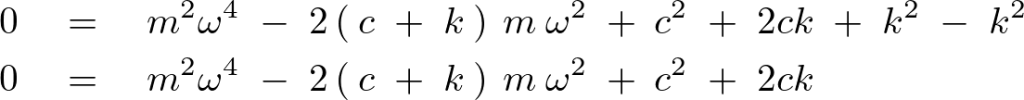
この式においてとおけば次に示すようなに対する2次方程式が出来上がります。

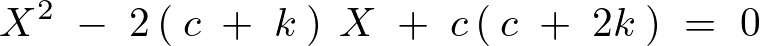
これを次のように計算していきます。

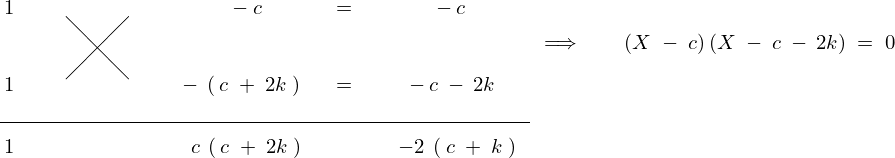
これよりをもとに戻せば以下の解が求まります。

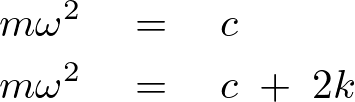
ここで上記の求まった解を区別するために以下のようにおきます。

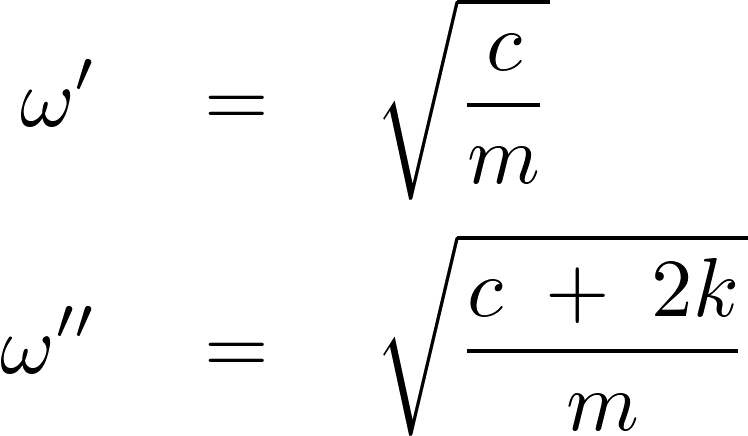
を代入すると、

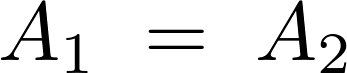
またを代入すれば、

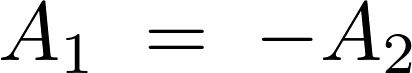
したがって、

の４つとも解になるのでそれぞれを代入します。

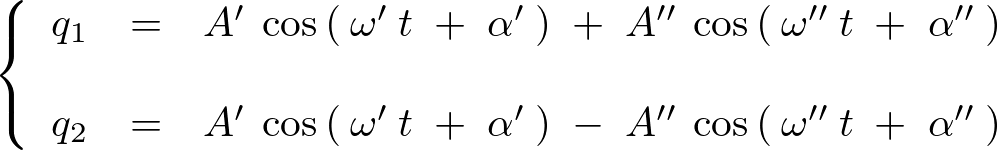
これが一般解になります。

、およびの与える解はなので距離を変えずに左右に振動する運動。

また一方では逆方向の運動と考えられます。