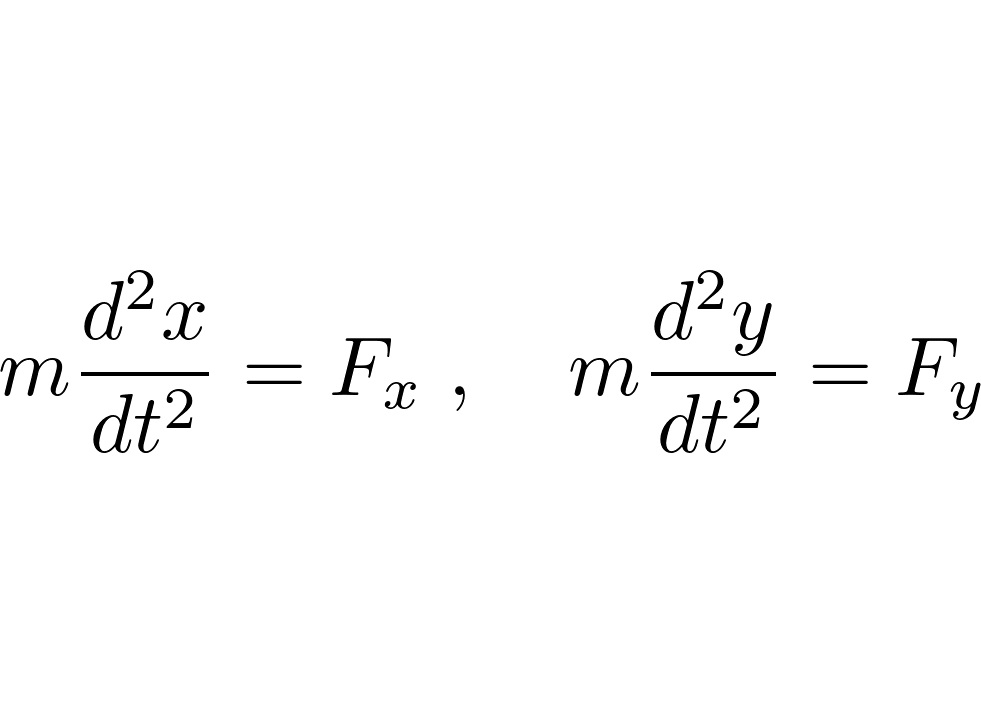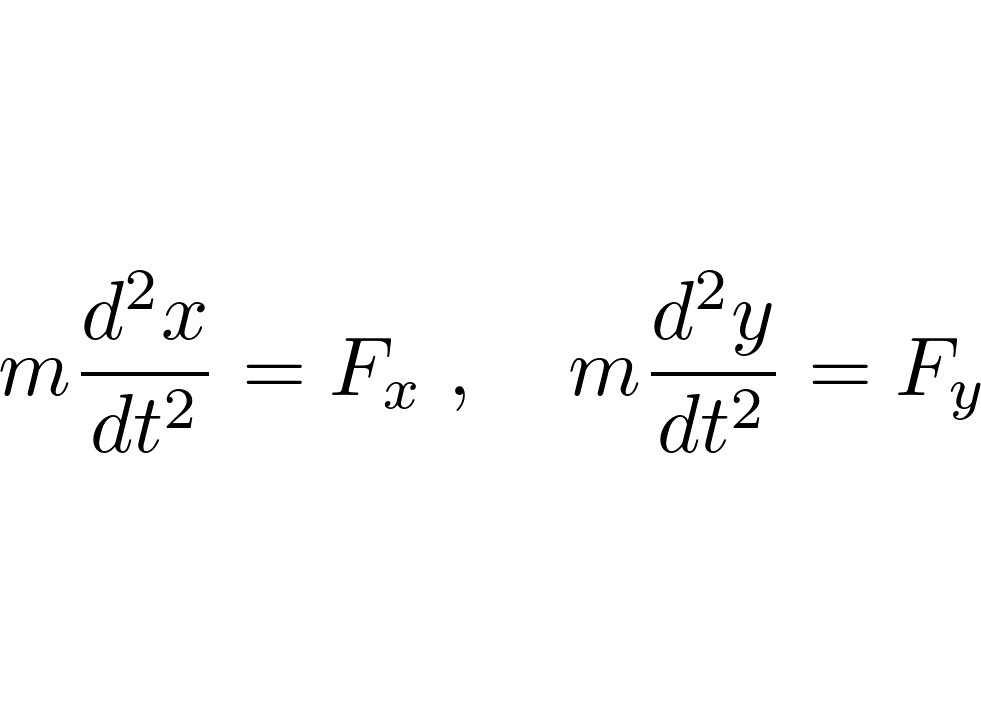ラグランジュの運動方程式
運動方程式の一般化
デカルト座標においての運動方程式の座標成分は、
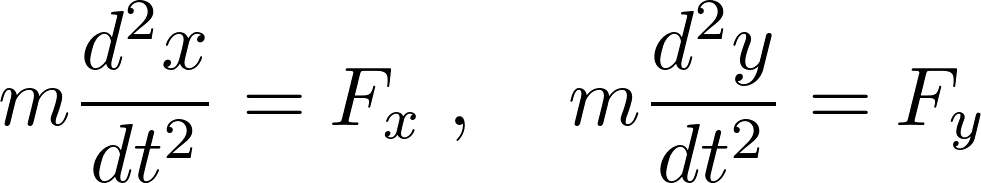
同じ運動を極座標系の動径方法と方位角方向のそれぞれで表せば、
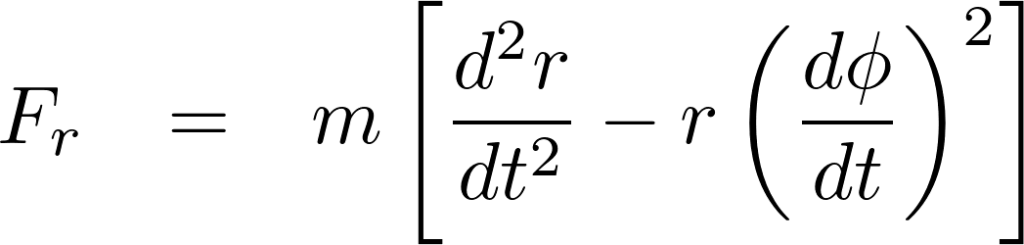

この運動を別の形で表現してみましょう。
運動方程式の変換
座標系においてある質量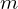 の平面運動について考えます。
の平面運動について考えます。
この質点にある力![]() が働き、そのために微小変化
が働き、そのために微小変化![]() が加わったとします。
が加わったとします。
この時に作用した力による微小仕事は、

で与えられます。
ベクトルをそれぞれ分解して表せば次のような式が求まることになります。
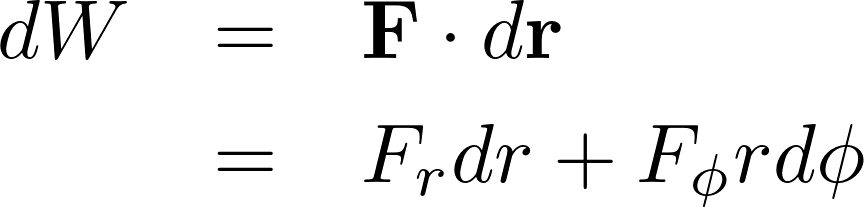
ここで上記式の![]() と
と![]() をそれぞれ
をそれぞれ![]() 、
、![]() と置きます。
と置きます。
すると、
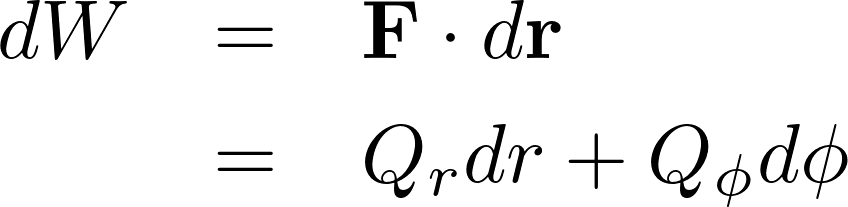
と表現できます。
この時の![]() 、
、![]() を一般化力といいます。
を一般化力といいます。
運動量は![]() だったのでそれぞれの力に分解すれば、
だったのでそれぞれの力に分解すれば、
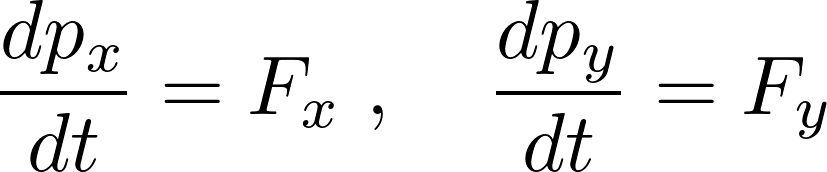
いまここで運動エネルギーについて考えると、

なのでこの式より、

となります。
したがって次のように表現できることになります。

極座標において速度ベクトル![]() は、
は、
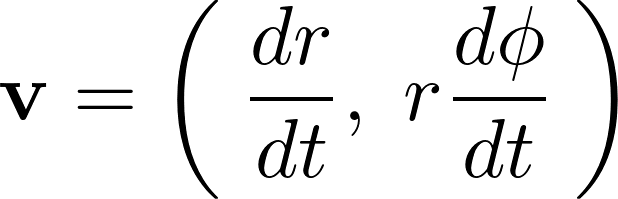
と表せるので、運動エネルギー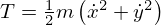 に関しては、
に関しては、
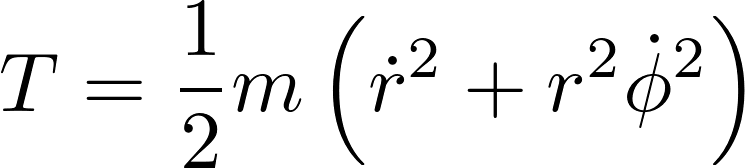
これにより、
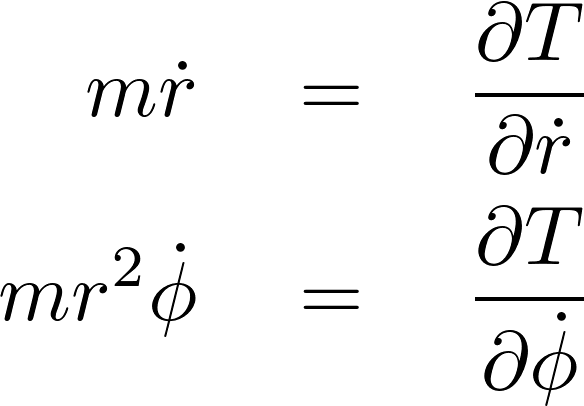
ここで上記運動方程式を時間![]() でそれぞれ微分します。
でそれぞれ微分します。
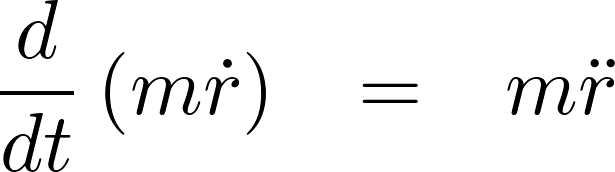
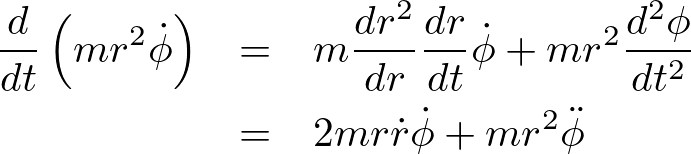
かつ、

これらの式をそれぞれ照らし合わせれば次のように表すことができます。
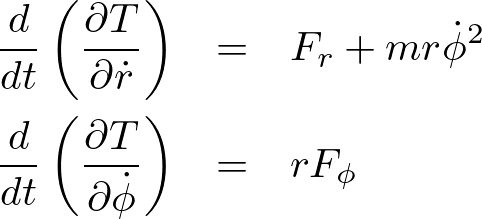
ここで![]() の式に着目してみると外力
の式に着目してみると外力![]() のほかに
のほかに![]() というのが含まれています。
というのが含まれています。
この式の右辺を![]() とすると、
とすると、
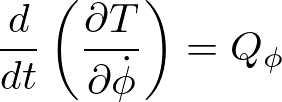
また、

であることを考慮すれば、
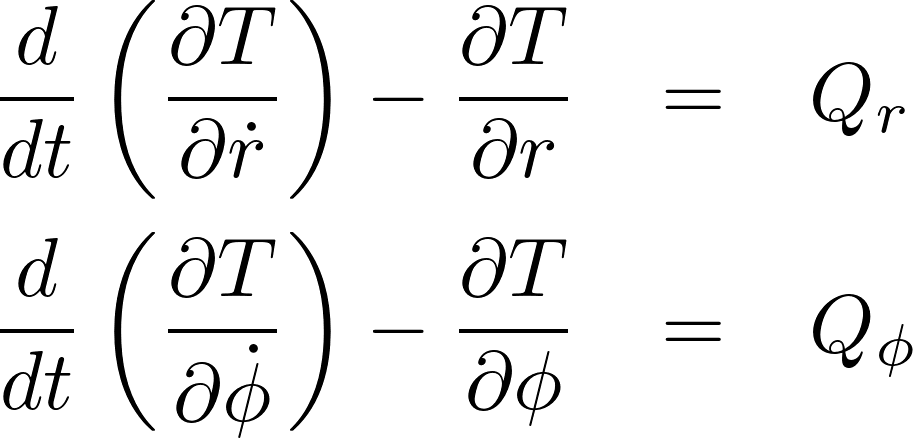
これにより以下のような関係式が求まります。

一般化座標と一般化力
デカルト座標に代わってすべての質点系の位置を特定するのに用いられる変数群を一般化座標といいます。
デカルト座標と一般化座標の間には座標変換に伴う変数関係、
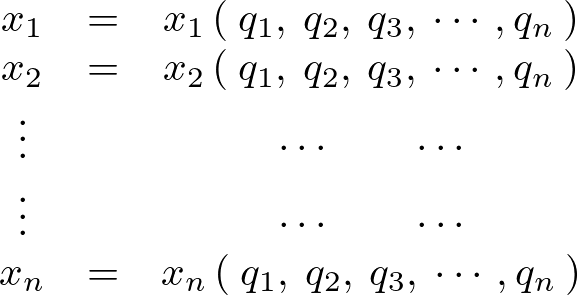
があり、上記の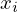 を時間で微分すると次のようになります。
を時間で微分すると次のようになります。

デカルト座標系の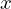 は時間の関数であるので一連の座標変換により(
は時間の関数であるので一連の座標変換により(![]() も時間の関数
も時間の関数![]() )、
)、![]() は
は![]() の関数になるためにこのような微分表現になります。
の関数になるためにこのような微分表現になります。
いま、質点系の各質点が微小変化し![]() が
が![]() になったとします。
になったとします。
このときの![]() の変化は、
の変化は、
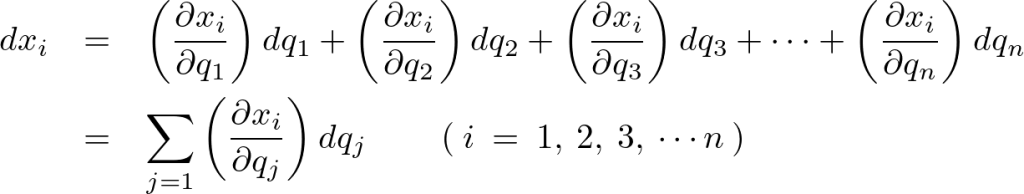
この変位に対して力のする仕事は、
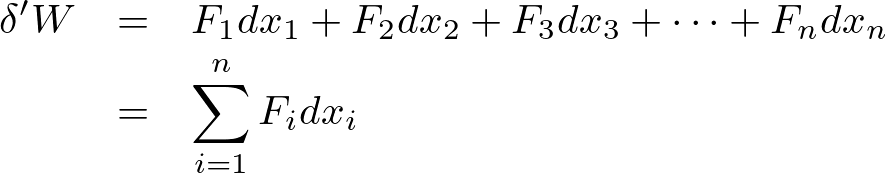
先ほどの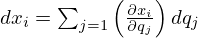 を代入すれば、
を代入すれば、

ここで、
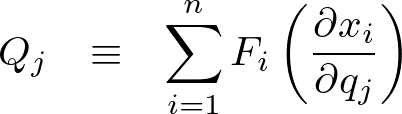
とおけば、
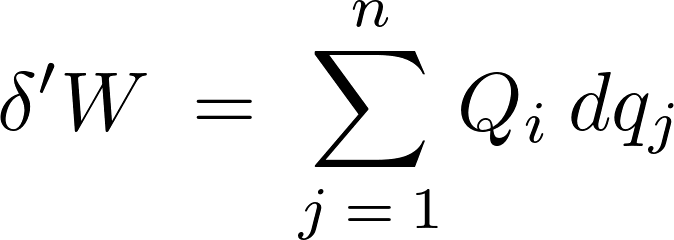
この![]() のことを一般化座標における一般化力といいます。
のことを一般化座標における一般化力といいます。

Title Text
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.